О бинарных операциях в многозначных логиках.

    Евсеев В.И, канд. физ.-мат. наук, доцент,

    ведущий научный сотрудник ЦСРМ, г. Казань

   УДК 681.32    

   Аннотация:

Данная статья посвящена классификации бинарных операций конъюнктивного типа, возникающих в многозначных логических системах для случаев трех, четырех и  пяти  различных классов истинности.

Ключевые слова: логическая система, классы истинности, отделяющие функции классов .

Abstract:

This article focuses on the classification of kon″ûnktivnogo type of binary operations that occur in themultivalued logical systems for three, four and fivedifferent classes of truth.

Keywords: logic, truth, separating the functions ofclasses classes.

 

1.     Классы истинности и отделяющие функции.

 

Мы будем обозначать эти классы традиционным способом:

а) для трехзначной логической системы это классы  ,  ;

б) для четырехзначной логической системы – классы ,, , ;

в) для пятизначной логической системы – классы ,, ,, .

Во всех вариантах класс называется (абсолютной) истиной, класс – относительной истиной, класс   – неопределенностью, класс  – относительной ложью, класс   –  (абсолютной) ложью.

Каждая логическая система может быть охарактеризована  соответствующими значениями логического параметра  в интервале

Для трехзначной логической системы эти значения обозначим по их убыванию ,  В этом случае  строится характеристическое уравнение:

.                                                                                              ( 1)

С помощью этого уравнения находятся отделяющие функции классов истинности:

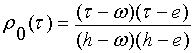,  для класса  ,                                           (2)    

 

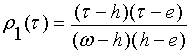    , для класса  ,                                                   (3)

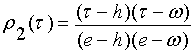, для класса  .                                              (4)

Для четырехзначной логической системыэти значения обозначим по их убыванию , при  этом характеристическое уравнение записывается формулой

                                             (5)

а отделяющие функции классов принимают вид:

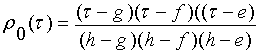 ,для класса ,                                                             (6)

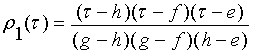 , для класса ,                                    (7)

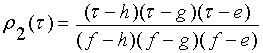 , для  класса  ,                                       (8)

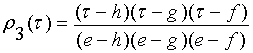, для класса  .                                    (9)

Для пятизначной логической системы с набором параметров характеристическое уравнение принимает вид

,

поэтому определяются следующие отделяющие функции логических классов:

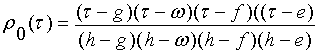 , для класса ,                               (10)

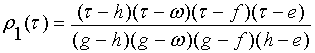 , для класса ,                              (11)

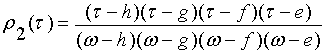 , для класса  ,                            (12)

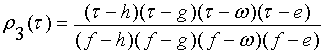 , для класса ,                            (13)

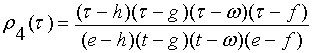, для класса .                                 (14)

2.     Бинарные операции трехзначной логики

 

Для логической системы бинарные операции конъюнктивного типа распределяются на следующие группы:

а) фортъюнкции (наиболее «сильные» по воздействию) могут быть трех видов

 

  Класс

 

№

 

Тип

Наименование

1

 

3

3

3

абсолютная

фортъюнкция

2

 

4

3

2

базовая

фортъюнкция

3

 

5

2

2

стандартная

фортъюнкция

 

б) Остальные бинарные операции входят  по одному разу:

 

 

  Класс

 

№

 

Тип

Наименование

4

 

4

4

1

субъюнкция

2

 

5

3

1

стандартная конъюнкция

3

 

6

2

1

панъюнкция

4

 

7

1

1

альтъюнкция

 

Из этих бинарных операций изученной нам представляется только стандартная конъюнкция, и то недостаточно, а остальные фактически никем не рассматривались.

3.     Бинарные операции четырехзначной логики

У четырехзначной логической системы определяется 34 различные бинарные операции конъюнктивного типа, которые мы зададим таблично.

         а) Фортъюнкции составляют следующие пять бинарных операций:

 

  Класс

 

№

 

Тип

1

 

4

4

4

4

2

 

5

4

4

3

3

 

5

5

3

3

4

 

6

4

3

3

5

 

7

3

3

3

 

У этих БОКТ (бинарных операций конъюнктивного типа) большое количество значений типа , что говорит об их логической силе, и, соответственно, достаточном количестве информации для обоснования.

б) субъюнкции имеют  восемь возможностей:

 

  Класс

 

№

 

Тип

6

 

6

4

4

2

7

 

5

5

4

2

8

 

6

5

3

2

9

 

7

4

3

2

10

 

8

3

3

2

11

 

8

4

2

2

12

 

7

5

2

2

13

 

6

6

2

2

14

9

3

2

2

15

10

2

2

2

 

 

Субъюнкции являются вторыми по логической силе после фортъюнкций, и у них заметно большее разнообразие составляющих эту группу БОКТ. Отметим, что у них одинаковое (по два) вхождение  общепозитивных суждений  вида А. Таким образом, мы переходим к группе стандартных по типу суждений, у которых общепозитивный вариант возможен только в одном случае. Эти БОКТ называются стандартными, в эту группу входят как стандартная, так и комплементарная конъюнкции.

В этой группе семь представителей.

 

в) Стандартные БОКТ

           

  Класс

 

№

 

Тип

16

 

 

5

5

5

1

17

 

6

5

4

1

18

 

7

4

3

1

19

 

7

5

3

1

20

 

8

4

3

1

21

 

6

6

3

1

22

 

9

3

3

1

 

 

Из таблицы видно, что стандартная конъюнкция имеет номер , а комплементарная конъюнкция номер . Остальные случаи отличаются единственным присутствием общепозитивного типа суждений.

Панъюнкции в четырехзначной системе характеризуются тем, что класс всюду входит  дважды, а класс только один раз.

Таких случаев в четырехмерном случае всего пять.

Построим для них отдельную таблицу.

г) панъюнкции.

 

 

  Класс

 

№

 

Тип

23

 

7

6

2

1

24

 

8

5

2

1

25

 

9

4

2

1

26

 

10

3

2

1

27

 

11

2

2

1

 

Последнюю группу из семи случаев составляют альтъюнкции.

           д) альтъюнкции  

 

  Класс

 

№

 

Тип

28

 

 

7

7

1

1

29

 

8

6

1

1

30

 

9

5

1

1

31

 

10

4

1

1

32

 

11

3

1

1

33

 

12

2

1

1

34

 

13

1

1

1

 

 

4.     Бинарные операции пятизначной логики

 

Эта логическая система содержит сто семьдесят пять БОКТ, которые также распределяются по различным группам, но и самих групп здесь гораздо больше.

а) фортъюнкции.

 

  Класс

 

№

 

Тип

1

5

5

5

5

5

2

 

6

5

5

5

4

3

 

6

6

5

4

4

4

 

7

5

5

4

4

5

 

7

6

4

4

4

6

 

8

5

4

4

4

7

 

9

4

4

4

4

 

Это самые мощные бинарные операции среди БОКТ.

Бинарные операции следующей группы впервые появляются в нашем описании. Они похожи на фортъюнкции для трехзначной системы, но здесь применяется пятимерная квадратная матрица, поэтому возможностей и вариантов здесь гораздо больше, хотя класс всюду входит в количестве трех представителей.

Представители второй  группы называются трансъюнкциями. Они также никем не изучались, их насчитывается 25 случаев.

                  б) трансъюнкции.

   Класс

 

№

 

Тип

8

7

5

5

5

3

9

8

5

5

4

3

10

6

6

6

4

3

11

7

6

5

4

3

12

8

5

5

4

3

13

7

7

4

4

3

14

8

6

4

4

3

15

9

5

4

4

3

16

7

7

5

3

3

17

6

6

5

5

3

18

9

5

5

3

3

19

8

7

4

3

3

20

7

6

6

4

2

21

7

6

6

3

3

22

8

6

5

3

3

23

8

8

3

3

3

24

9

5

5

3

3

25

9

6

4

3

3

26

9

7

3

3

3

27

10

5

4

3

3

28

10

4

4

4

3

29

11

4

4

3

3

30

11

5

3

3

3

31

12

4

3

3

3

32

13

3

3

3

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Субъюнкции характеризуются тем, что класс относительной истины присутствует в количестве, большем двух, а классвходит всюду дважды.

Их насчитывается 20 конкретных вариантов.

в) Субъюнкции

    Класс

 

№

 

Тип

33

6

6

6

5

2

34

7

6

5

5

2

35

8

5

5

5

2

36

7

6

6

4

2

37

7

7

5

4

2

38

8

6

5

4

2

39

9

5

5

4

2

40

8

7

4

4

2

41

9

6

4

4

2

42

10

5

4

4

2

43

11

4

4

4

2

44

7

7

6

3

2

45

8

7

5

3

2

46

9

6

5

3

2

47

10

5

5

3

2

48

8

8

4

3

2

49

9

7

4

3

2

50

10

6

4

3

2

51

11

5

4

3

2

52

12

4

4

3

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Следующая совокупность группы имеет непривычное название «теръюнкция». В нее входит 18 конкретных вариантов. Она характеризуется точно двумя вхождениями классов и .

г) теръюнкции.

    Класс

 

№

 

Тип

53

7

7

7

2

2

54

8

7

6

2

2

55

8

8

5

2

2

56

9

7

5

2

2

57

10

6

5

2

2

58

11

5

5

2

2

59

9

8

4

2

2

60

10

7

4

2

2

61

11

6

4

2

2

62

12

5

4

2

2

63

13

4

4

2

2

64

9

9

3

2

2

65

10

8

3

2

2

66

11

7

3

2

2

67

12

6

3

2

2

68

13

5

3

2

2

69

14

4

3

2

2

70

15

3

3

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Остальные группы по содержанию напоминают традиционную конъюнкцию, так как являются по своей сути стандартными и содержат только одно вхождение класса истины . В первой из таких групп вхождение класса относительной истины  всюду больше двух. Мы назовем этот набор «тенъюнкцией». В этом наборе всего 32 конкретных варианта.

д) тенъюнкции.

  Класс

 

№

 

Тип

71

6

6

6

6

1

72

7

6

6

5

1

73

7

7

5

5

1

74

8

6

5

5

1

75

9

5

5

5

1

76

7

7

6

4

1

77

8

7

5

4

1

78

8

8

4

4

1

79

9

7

4

4

1

80

10

6

4

4

1

81

11

5

4

4

1

82

12

4

4

4

1

83

9

6

5

4

1

8

8

7

6

3

1

85

9

6

6

3

1

86

8

8

5

3

1

87*

9

7

5

3

1

88

10

6

5

3

1

89

11

5

5

3

1

90

9

8

4

3

1

91

10

7

4

3

1

92

11

6

4

3

1

93

12

5

4

3

1

94

13

4

4

3

1

95

7

7

7

3

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

д) тенъюнкции (окончание).

 

  Класс

 

№

 

Тип

96

9

9

3

3

1

97

10

8

3

3

1

98

11

7

3

3

1

99

12

6

3

3

1

100

13

5

3

3

1

101

14

4

3

3

1

102

15

3

3

3

1

 

 

 

 

 

 

 

 

Следующий набор групп характеризуется точными значениями:

для класса их число равно двум, а для классаединице. Эта группа операций называется панъюкциями. Она содержит 30 вариантов.

е) панъюнкции.

     Класс

№

Тип

103

8

8

6

2

1

104

8

7

7

2

1

105

9

7

6

2

1

106

10

6

6

2

1

107

9

8

5

2

1

108

10

7

5

2

1

109

11

6

5

2

1

110

12

5

5

2

1

111

9

9

4

2

1

112

10

8

4

2

1

113

11

7

4

2

1

 

 

 

 

 

 

 

 

 

 

 

 

                  е) панъюнкции (окончание).

 

      класс

№

Тип

114

12

6

4

2

1

115

13

5

4

2

1

116

14

4

4

2

1

117

10

9

3

2

1

118

11

8

3

2

1

119

12

7

3

2

1

120

13

6

3

2

1

121

14

5

3

2

1

122

15

4

3

2

1

123

16

3

3

2

1

124

10

10

2

2

1

125

11

9

2

1

1

126

12

8

2

2

1

127

13

7

2

2

1

128

14

6

2

2

1

129

15

5

2

2

1

130

16

4

2

2

1

131

17

3

2

2

1

132

18

2

2

2

1

 

В остальных вариантах бинарных операций конъюнктивного типа для пятизначной логической системы значения классов и постоянно равны единице. Все эти возможности условно подразделены на две подгруппы: мальюнкции и альтюнкции. Рассмотрим их последовательно. В первой подгруппе   23   варианта, а во второй  – 20  вариантов.

 

ж) Мальюнкции.

       класс

№

Тип

133

8

8

7

1

1

134

9

7

7

1

1

135

9

8

6

1

1

136

10

7

6

1

1

137

11

6

6

1

1

138

9

9

5

1

1

139

10

8

5

1

1

140

11

7

5

1

1

141

12

6

5

1

1

142

13

5

5

1

1

143

10

9

4

1

1

144

11

8

4

1

1

145

12

7

4

1

1

146

14

5

4

1

1

147

15

4

4

1

1

148

10

10

3

1

1

149

11

9

3

1

1

150

12

8

3

1

1

151

13

7

3

1

1

152

14

6

3

1

1

153

15

5

3

1

1

154

16

4

3

1

1

155

17

3

3

1

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Последняя подгруппа в этой системе – это альтъюнкция, у которой по одному значению классов и , а класс  представлен сначала двумя значениями, а потом – одним.

 

з) Альтъюнкция.

         класс

№

Тип

156

11

10

2

1

1

157

12

9

2

1

1

158

13

8

2

1

1

159

14

7

2

1

1

160

15

6

2

1

1

161

16

5

2

1

1

162

17

4

2

1

1

163

18

3

2

1

1

164

19

2

2

1

1

165

11

11

1

1

1

166

12

10

1

1

1

167

13

9

1

1

1

168

14

8

1

1

1

169

15

7

1

1

1

170

16

6

1

1

1

171

17

5

1

1

1

172

18

4

1

1

1

173

19

3

1

1

1

174

20

2

1

1

1

175

21

1

1

1

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Таким образом, нами построены полные системы бинарных операций конъюнктивного типа для трех уровней многозначных логических систем – трехзначной, четырехзначной  пятизначной логик.  Всего их оказалось 175 БОКТ, которых распределяются по логически обусловленным частям. Теперь нами подготовлен математический аппарат для изучения всех конкретных случаев этих систем. Для этого достаточно только научиться отыскивать виды конкретных логических формул в зависимости от вида групп и операций в них. Следует заметить, что приведенные формулы отделяющих функций соответствуют «нулевым зонам», где значения чисел вхождения логических классов различен для всех видов классов истинности. Для других случаев мы предлагаем модернизацию этих  функций, что еще ожидает своего завершающего исследования. По крайнем мере, результаты нашей монографии 

позволяют выполнить эту работу в будущем.

      

             Литература:

1.     Евсеев В.И. Логическое обоснование семантических структур //Феномены природы и экология человека. Материалы пятого Международного симпозиума, т. 3 (94 – 101) Казань. 2008.

2.     Евсеев В.И. Конструктивная комплементарная семантика. Монография. Изд – во «». 2014 г.

3.     Евсеев В.И. Об основных принципах моделирования логической семантики// Труды международной научно-практической конференции «ИТОН – 2012). Изд-во К(П)ФУ. Казань, 2012 г (221 – 225)

4.     Евсеев В.И. Основы аналитической семантики         . Монография. Изд – во «». 2014 г.