ПОЗИЦИИ И
ФОРМУЛЫ МАЛЫХ ЛОГИЧЕСКИХ ФИГУР
Евсеев В.И, канд. физ.-мат. наук, доцент,
г.
Казань, РТ
УДК 681.32
Аннотация:
Эти заметки призваны
продемонстрировать методику работы с логическими фигурами, которая в дальнейшем
будет основой изложения во всех материалах, связанных с фигурными комплексами.
Ключевые слова:
полигоны, фигуры и оболочки, позиции фигур, логические линии, формулы фигур.
These notes are intended to demonstrate a methodology for working with
Boolean shape which will later be the basis of all content related to curly
complexes. Key words: polygons, shapes and positions of the hull shapes,
logical lines, forms of formula.
1.
Позиции малых логических
фигур
Напомним, что малые
логические фигуры состоят из одной,
двух или трех «склеенных» клеток, погруженных в полигон прямоугольного вида,
содержащий также всю их оболочку. Кроме того, на полигоне могут оставаться
нерабочие пустые клетки, соответствующие для логических фигур пустому
множеству, которое при записи формул этих фигур не учитывается, а в логической
матрице обозначается значком Ø.
Наименьшая логическая фигура состоит из одной
клетки и называется униада, она вместе
с оболочкой погружается в полигон
.
Эта фигура обозначается 
,
и в результате мы получаем схему:
|
▒ |
▒ |
▒ |
|
▒ |
|
▒ |
|
▒ |
▒ |
▒ |
В дальнейшем мы не будем
вписывать в таблицу изображений символ фигуры, так как он будет понятен по
изображению.
Второй малой фигурой
является диада 
,
она может иметь две позиции – горизонтальную 
и
вертикальную 
.
Горизонтальная диада
имеет изображение на полигоне 
:
|
▒ |
▒ |
▒ |
▒ |
|
▒ |
|
|
▒ |
|
▒ |
▒ |
▒ |
▒ |
Вертикальная позиция
изображается
на полигоне 
|
▒ |
▒ |
▒ |
|
▒ |
|
▒ |
|
▒ |
|
▒ |
|
▒ |
▒ |
▒ |
Третьей малой фигурой
является триада, которая имеет две разновидности, первая – линейная – обозначается символом 
, а вторая имеет символ 
и называется угловой. Линейная триада может иметь две
позиции: вертикальную и горизонтальную. Горизонтальная позиция линейной диады 
принадлежит (вместе с оболочкой) полигону 
:
|
▒ |
▒ |
▒ |
▒ |
▒ |
|
▒ |
|
|
|
▒ |
|
▒ |
▒ |
▒ |
▒ |
▒ |
Хотим заметить, что эти
фигуры не имеют пустот на полигоне, так как оболочка полностью адаптирована с
фигурой и полигоном. Следующая позиция также обладает этим свойством.
Вертикальная позиция
линейной триады 
вместе со своей оболочкой принадлежит полигону 
:
|
▒ |
▒ |
▒ |
|
▒ |
|
▒ |
|
▒ |
|
▒ |
|
▒ |
|
▒ |
|
▒ |
▒ |
▒ |
Угловая триада 
допускает четыре
различных позиции, причем все они
со своими оболочками принадлежат полигону 
, а также имеют по одной пустой клетке в каждом случае. В
качестве первой позиции угловой 
триады выбираем
фигуру:
|
▒ |
▒ |
▒ |
▒ |
|
▒ |
|
|
▒ |
|
▒ |
|
▒ |
▒ |
|
▒ |
▒ |
▒ |
|
Вторая позиция 
получается из первой поворотом на +
:
|
▒ |
▒ |
▒ |
|
|
▒ |
|
▒ |
▒ |
|
▒ |
|
|
▒ |
|
▒ |
▒ |
▒ |
▒ |
Третья позиция 
также является
результатом указанного поворота из предыдущей позиции:
|
|
▒ |
▒ |
▒ |
|
▒ |
▒ |
|
▒ |
|
▒ |
|
|
▒ |
|
▒ |
▒ |
▒ |
▒ |
Последний для этой
фигуры поворот приводит к позиции 
:
|
▒ |
▒ |
▒ |
▒ |
|
▒ |
|
|
▒ |
|
▒ |
▒ |
|
▒ |
|
|
▒ |
▒ |
▒ |
2.
Формулы логических диад
Как мы уже отмечали, для
построения формул логических фигур применяется матричный метод, в котором
участвуют два типа высказываний: 
и 
, а также их отрицания, при этом первые из них
характеризуются вертикальным столбцом значений, а вторые – вертикальной
строкой. В зависимости от вида вмещающего полигона матрица значений имеет
собственное квадратное строение. Размер стороны квадрата этой матрицы на
единицу меньше суммы размерностей матрицы полигона, то есть, если полигон имеет
вид 
, то размер квадрата логической матрицы равен:
. (1)
Прежде всего, в этой матрице выделяется правый
нижний блок, соответствующий изображению вмещающего полигона фигуры с ее
оболочкой в рассматриваемой позиции, затем строятся «несущие» вертикальные и
горизонтальные значения логических переменных (
,
), после этого диагональным методом в левом нижнем блоке
изображаются переменные типа 
, причем четные ставятся сразу с
отрицаниями . Затем устанавливаются высказывания типа 
в вернем правом блоке, также с учетом отрицания по четным
значениям. В самом изображении полигона выделенная серым цветом на изображении
позиции фигура отмечается единицами, клетки оболочки указываются нулями, а
пустые клетки (если они имеются) отмечаются символом пустого множества и в
дальнейшем анализе участия не принимают.
Мы снова вынуждены применять методику «больших
матриц», которая успешно работала в
общей семантической теории (см. 
. Эта
методика и в данном случае оказывается эффективной.
Построим логическую матрицу для наименьшей
фигуры 
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
|
|
|
0 |
0 |
0 |
0 |
1 2 2 3 |
|
|
1 |
0 |
1 |
0 |
|
|
|
0 |
0 |
0 |
0 |
Введем понятие линии как соединения двух соседних строчек логической матрицы. Линии будем
обозначать символом 
, с применением римских цифр, так для этого примера получаем: 
, 
. Получается, что число линий на единицу меньше числа строк
логической матрицы. Каждая линия представляет собой дизъюнкцию бинарных
операций, определенных парами проходимых столбцов (слева направо). Так для
этого случая получаем:
, (2)
. (3)
Исходные матрицы формул бинарных операций даны в
монографии 
(стр. 14). Применение
отрицаний приводит к соответствующему
изменению указанных в монографии формул. Так, по указанной ссылке, с учетом,
что нами рассматривается категорическая логика (
,
получаем для
данного примера:
,
, (4)
Значит, в реальности для первой линии получаем:
.
(5)
Аналогично вычисляется и вторая линия:
,
. (6)
Поэтому
. (7)
Таким образом, находим всю формулу этой фигуры
. (8)
Следовательно, можно определить область истинности изучаемой
фигуры
(9)
Столь подробный анализ для других фигур мы в
данной статье проводить не будем, оставив этот материал для будущей монографии. А здесь в каждом случае будем находить
только сами формулы указанных позиций фигур.
Для горизонтальной позиции 
диады определяется
логическая матрица
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
0 |
0 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
Здесь мы не указываем нумерацию линий,
предполагая ее известной.
Также как и в предыдущем случае, получаем две
линии, то есть:
. (10)
Первая линия характеризуется формулой
, (11)
а формула второй линии имеет вид:
. (12)
Отметим рабочие формулы для операции трап:
, 
,
,
. (13)
Подставляя результаты (12) и (13) в формулу
(10), находим вид всей логической формулы этой фигуры.
(14)
Для вертикальной позиции диады 
получается
матрица
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
|
|
|
0 |
0 |
0 |
0 |
|
|
|
1 |
0 |
1 |
0 |
|
|
|
0 |
0 |
1 |
0 |
|
|
|
1 |
0 |
0 |
0 |
В данном случае
логическая матрица имеет три линии:
. (15)
При линейном прохождении получаем их формулы:
=
, (16)
=
, (17)
=
. (18)
3.
Формулы логических триад
Теперь укажем логические матрицы и формулы
триад. Линейная триада как уже было отмечено, имеет две позиции. Для ее
горизонтальной позиции 
находим такую логическую матрицу
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
Укажем только содержание двух линий, из которых
как дизъюнкция получается формула всей
этой фигуры:
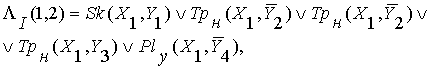(19)
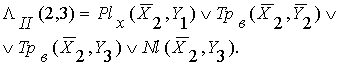(20)
Мы не будем здесь приводить окончательный
результат, а перейдем к угловой триаде 
, которая имеет четыре различных позиции, а в ее формуле присутствует пустое
множество, так как на полигонах есть ничем не заполненные клетки.
Первая позиция этой угловой триады 
имеет логическую матрицу
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
1 |
0 |
1 |
1 |
0 |
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
1 |
0 |
0 |
0 |
Ø |
Значит, ее формула состоит из трех линий, и при
этом пустое множество просто удаляется из этой формулы. Формулы линий здесь
имеют вид:
=
(21)
= 
(22)
=
(23)
Значит:
. (24)
Логическая матрица для второй позиции угловой
триады 
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
0 |
0 |
0 |
0 |
Ø |
|
|
|
1 |
0 |
1 |
0 |
0 |
|
|
|
0 |
0 |
1 |
1 |
0 |
|
|
|
1 |
0 |
0 |
0 |
0 |
С ее помощью находим формулы линий для этой
матрицы:
=
(25)
=
(26)
=
(27)
Следовательно, в этом случае получаем логическую
формулу:
. (28)
Перейдем к следующей позиции этой фигуры 
.
Логическая матрица этой позиции такая:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
0 |
Ø |
0 |
0 |
0 |
|
|
|
1 |
0 |
0 |
1 |
0 |
|
|
|
0 |
0 |
1 |
1 |
0 |
|
|
|
1 |
0 |
0 |
0 |
0 |
Формула для этой позиции также характеризуется
тремя линиями:
. (29)
В данном случае:
=
(30)
=
(31)
=
(32)
Последняя из возможных позиций 
характеризуется матрицей:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
1 |
0 |
1 |
1 |
0 |
|
|
|
0 |
0 |
0 |
1 |
0 |
|
|
|
1 |
Ø |
0 |
0 |
0 |
Ее формула также содержит три линии.
Укажем сразу сами эти линии.
=
(33)
=
(34)
=
(35)
Конечно, в каждом случае можно найти область
истинности всей формулы как объединение соответствующих областей составляющих
линий. Эта довольно трудоемкая работа, и мы ее выполним для будущей монографии.
Цель этой статьи, как нам кажется выполнена.
Литература:
1. Евсеев В.И.
Конструктивная комплементарная семантика. Монография. Изд-во «Ламберт». 2014 г.
2. Евсеев В.И. Аспекты
информознания //Труды международной научно-практической конференции «Новости
передовой науки». Т.12 . 2014 г.(63-74).
3. Евсеев В.И. О типологии
уровней бинарных операций// Труды международной научно-практической конференции
«Новости передовой науки», т.27. 2014 г. (50 – 57).