К.ф.-м.н. Постников Б.М.

Северный государственный медицинский университет, Россия

Уравнение связи между внутренним радиусом кровеносного сосуда и давлением крови

Светлой памяти

замечательного физика

и прекраснейшего человека

С.Е. Ефимовского посвящаю

1. Постановка задачи

Пусть внутренний радиус кровеносного сосуда, толщина его стенки, механическое напряжение в стенке сосуда, т.е. отношение силы растяжения сосуда к площади его продольного сечения, давление крови, т.е. разность между её истинным давлением и атмосферным давлением (именно эта разность и расширяет кровеносный сосуд, давая крови возможность протекать по нему).

Известно следующее уравнение связи между введёнными выше величинами:

. (1)

Это уравнение (1) называют уравнением Ламе.

К сожалению, из уравнения (1) невозможно получить непосредственную связь между давлением крови и радиусом сосуда , т.к. мешают «посредники» и , которые сами являются переменными величинами. Эта непосредственная связь между и , конечно же, должна существовать априорно. Поэтому поставим задачу её найти. Например, можно попытаться найти либо функциональную зависимость от (функцию , либо функциональную зависимость от (функцию .

2. Решение задачи

Будем полагать, что при растяжении кровеносного сосуда плотность его стенки не изменяется, а, значит, не изменяется и её объём . Будем полагать, что и длина кровеносного сосуда тоже не изменяется. Тогда площадь поперечного сечения стенки кровеносного сосуда является константой. Очевидно, что (это равенство, вообще говоря, приближённое, но при малых оно практически точное). Значит, произведение также является константой. Обозначим её через , т.е. положим . Выражая отсюда и подставляя его в уравнение (1), получим следующую взаимосвязь:

. (2)

Уравнение (2) содержит только три переменные величины, т.е. мы избавились от одного лишнего «посредника» в уравнении (1).

Далее используем закон Гука:

где модуль упругости Юнга, относительная деформация. Тогда

Поскольку для цилиндра изменение относительной деформации , то

Интегрируя это простейшее дифференциальное уравнение, мы получаем, что

(3)

Пусть радиус кровеносного сосуда при (т.е. при «отсутствии» напряжения в стенке сосуда, что равносильно «отсутствию» давлению изнутри сосуда). По этому начальному условию (оно равносильно условию в силу уравнения (2)) найдём постоянную в выражении (3):

Поэтому получаем функцию (4)

Изобразим схематично график функции :

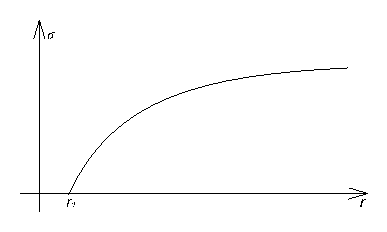
Рис. 1

Теперь уже легко находим функцию из уравнения (2) и равенства (4):

(5)

Исследуя полученную в виде (5) функцию с помощью её производной, мы найдём её точку максимума , причём наибольшее значение функции . Точкой перегиба функции является точка , . Поэтому график функции имеет следующий вид:

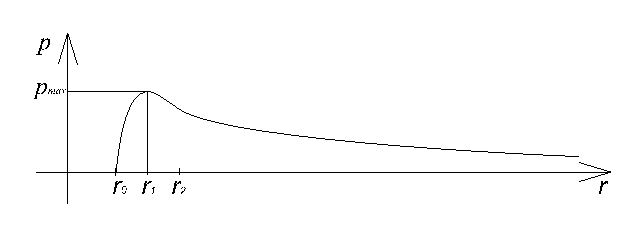
Рис. 2

Заметим, что функция при .

3. О другом дифференциальном уравнении с тем же решением и об истории постановки задачи

В [1] (см. формулу (10.20) на стр. 195) выведено следующее дифференциальное уравнение для функции :

(6)

Решение уравнения (6) в [1] не дано. Видимо автору не удалось получить явное аналитическое решение этого уравнения. Поэтому он предлагает при больших значениях модуля упругости заменить уравнение (6) на следующее его приближение:

(7)

Именно в связи с уравнением (6) и была поставлена сформулированная выше (в пункте 1) задача. Её поставил передо мной мой коллега, заведующий кафедрой медицинской и биологической физики СГМУ Сергей Евграфович Ефимовский. Он указал на отсутствие в [1] решения уравнения (6) и предложил мне (как математику) исследовать это уравнение и попытаться найти хотя бы приближённое его решение каким-либо методом. С первого (видимо, не очень внимательного) взгляда я не увидел в нём дифференциального уравнения какого-либо известного мне типа. Поэтому я подробно изучил в [1] процедуру вывода этого уравнения. Буквально через день, используя некоторые идеи из [1] (см. формулы (10.14), (10.16), (10.17) и (10.18)), я получил достаточно простой вывод функциональной зависимости , не использующий уравнения (6). Этот вывод и изложен в пункте 2 этой статьи. Затем непосредственной подстановкой полученной мною функции в виде (5) в дифференциальное уравнение (6) я убедился, что она является его решением. Тогда мне стало ясно, что уравнение (6) должно иметь явное аналитическое решение. Поглядев на него более внимательно и преобразовав его, я распознал в нём линейное дифференциальное уравнение относительно функции . Действительно, уравнение (6) преобразуется к виду:

Решая последнее уравнение методом вариации постоянной (методом Лагранжа) и учитывая начальное условие (см. пункт 2 этой статьи), мы получим, что Итак, более сложным и длинным путём находится та же самая функция , что и найденная в пункте 2 (см. (5)).

Обратимся теперь к уравнению (7). Его решение , удовлетворяющее начальному условию , имеет вид:

. (8)

Найдём значения и . Заметим также, что при функция Теперь схематично изобразим графики функций на одном рисунке (сверху график ):

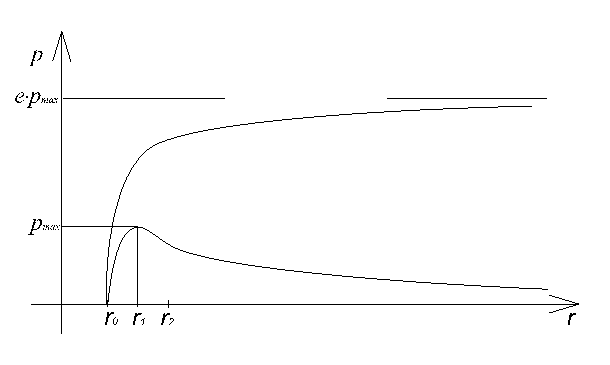
Рис. 3

Из этого рисунка мы видим, что предлагаемая в [1] замена дифференциального уравнения (6) на более простое дифференциальное уравнение (7) оказывается несостоятельной при любых значениях модуля упругости .

4. Об интерпретации и возможных применениях уравнения (5)

Истолкование уравнения (5) намеревался дать С.Е. Ефимовский, поставивший передо мной эту задачу. Но он не успел этого сделать. В 2013 году он, к глубокому сожалению всей нашей кафедры, после тяжёлой болезни ушёл из жизни в полном расцвете творческих сил.

Поэтому я решил опубликовать уравнение (5) с целью заинтересовать кого-либо в получении его экспериментального подтверждения и содержательной интерпретации, а также в поиске возможных его применений.

В заключение статьи я изложу (и немного разовью) одно соображение, высказанное мне С.Е. Ефимовским. Рассмотрим следующий простой и всем известный эксперимент. Будем медленно надувать воздушный шарик. Причём, лучше взять длинную воздушную колбаску, которая напоминает кровеносный сосуд и может служить его моделью. В некоторый момент шарик вдруг резко и самопроизвольно начинает расширяться. Этот факт хорошо согласуется с графиком функции (см. рисунок 2). Мы видим, что после достижения радиусом значения , при котором давление максимально (), дальнейшее увеличение радиуса сопровождается уменьшением давления . Поэтому можно предположить, что надуваемый шарик начинает самопроизвольно расширяться как раз с момента достижения в нём максимального давления , и при этом самопроизвольном расширении давление в нём падает. Тогда (согласно рисунку 2) и дальнейшее надувание шарика ведёт не к увеличению (как можно ошибочно предположить), а к уменьшению давления в нём. Теоретически при неограниченном росте радиуса шарика давление в нём уменьшаясь стремится к нулю. Но поскольку напряжение в его стенке хоть и медленно, но всё же растёт (см. (4) и рис. 1), то в некоторый момент шарик лопнет. Здесь, конечно, следует напомнить (см. начало пункта 1), что давление - это превышение истинного давления в нём над атмосферным давлением. Поэтому истинное давление в нём уменьшаясь стремится к атмосферному давлению.

Не в этом ли удивительном механизме кроется истинная причина возникновения таких патологий кровеносных сосудов как аневризма аорты, варикозное расширение вен и подобные им заболевания сосудов? Понятно, что ответ на этот вопрос потребует проведения серьёзных экспериментальных исследований. Но всё же хочется высказать несколько предположений по этому поводу. Достижение в кровеносном сосуде давления , и тем более его превышение, вызывает спонтанное и весьма значительное расширение сосуда. Возможно, что многократные повторения этой ситуации и провоцируют возникновение патологии. Чем меньше для сосуда величина , тем вероятнее возникновение его патологии.

Далее преобразуем выражение для . Учитывая, что константа и площадь поперечного сечения стенки кровеносного сосуда (см. пункт 2), мы получим:

,

где абсолютная константа, а константы , и являются характеристиками (параметрами) кровеносного сосуда. Таким образом, чем у сосуда меньше площадь поперечного сечения стенки и модуль упругости и чем больше радиус , тем вероятнее возникновение патологии в нём.

Литература:

1. Ремизов А.Н. Медицинская и биологическая физика.- М.: ГЭОТАР - Медиа, 2012. - 648 с.