УДК
624.012.35.046
Байнатов
Ж.Б.
д.т.н.,
профессор Казахский национальный технический университет им.К.И. Сатпаева, Казахстан
Мурзалина
Г.Б.
к.т.н.,
доцент КазНТУ им.К.И. Сатпаева,
Казахстан
Жалғасбекова С.Ж.
студентка КазНТУ им.К.И. Сатпаева, Казахстан
ОПРЕДЕЛЕНИЕ НЕСУЩЕЙ СПОСОБНОСТИ СТЕРЖНЕВЫХ СИСТЕМ ПРИ СЛОЖНОМ МЕХАНИЗМЕ
РАЗРУШЕНИЯ
Расчет сооружений за пределом упругой работы материала
представляет исключительный интерес для инженера-конструктора, так как именно
неупругой стадией работы сооружения определяется его несущая способность.
Данную задачу
можно решать двумя способами. В первом кинематическом
способе необходимо прежде всего выявить все возможные схемы разрушения системы.
Для этого следует считать перешедшими в состояние пластической текучести столько связей системы, сколько необходимо
для превращения ее в изменяемую систему: механизм или кинематическую цепь. Это
превращение может быть произведено многими способами, и каждому из этих
способов, соответствующему определенной схеме разрушения, будет отвечать
определенное значение разрушающей нагрузки, необходимой для уравновешивание
внутренних усилий в связях, перешедших в состояние текучести
Второй способ
определения разрушающей нагрузки проф. Гвоздев называют статическим.
Здесь мы
исходим на различных возможных распределений внутренних усилий в статически
неопределимой системе, отвечающих заданной нагрузке.
Окончательное
уяснение принципов расчета упруго – пластических систем на разрушающую нагрузку
может быть сделано на примерах. Возьмем следующую систему. Абсолютно жесткая и
прочная балка укреплена на трех стержнях, как показано на рисунке 1 [1].
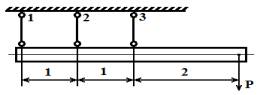
Рисунок 1. Абсолютно жесткая и
прочная балка, укрепленная на трех стержнях
Стержни могут
работать как на растяжение, так и на сжатие с пределом текучести σт=2500 кг/см2.
Площадь поперечного сечения каждого стержня равна 4 см2. Таким
образом предельные усилия сжатия и растяжения Sт для
каждого стержня равны +10т. Требуется определить разрушающую величину
нагрузки Р.
Рассчитаем эту же систему
статическим методом [2].
Возьмем
следующее состояние равновесия данной системы, отвечающее нагрузке
Р=1 (Рисунок 2)
S1=-1, S2=0, S3=2, (1)
и добавим к нему состояние самонапряжения,
соответствующее нагрузке Р=0
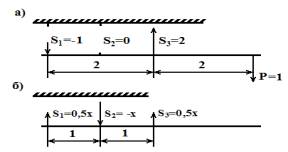
Рисунок
2. Состояние равновесия системы, отвечающее
нагрузке Р=1
S1=0,5Х, S2=-Х, S3=0,5Х, (2)
здесь
Х – множитель, который может принимать
любое значение. Так как система только один раз статически неопределима, то в
ней может возникнуть только это одно
состояние самонапряжения. Суммируя состояние равновесия (1) и (2), получаем для
единичной нагрузки
S1=-1+0,5Х, S2=-Х, S3=2+0,5Х.
Для каждого значения Х одно из усилий S1, S2, S3 будет
принимать наибольшее абсолютное значение. Разделив на него предельное
усилие Sт=10т, получим предельную нагрузку, которая
будет различна для различных значений Х.
Для того чтобы определить, какое именно
следует брать Х, чтобы предельная
нагрузка получилась наибольшей, построим график зависимости абсолютных значений
S1, S2 и S3 от Х. Такой график
представлен на рисунке 3.

Рисунок
3. График зависимости абсолютных
значений S1, S2 и S3 от Х
Из него легко видеть, что
наивыгоднейшее распределение усилий в
стержнях получается при Х=-1,
соответствующем точке пересечения графиков усилий S1 и S3. При
этом значении Х:
-S1 = S3 =1,5; S2=-1.
Отсюда
разрушающая нагрузка получается равной
Рразр=![]() =6,67т.
=6,67т.
Расчет статически неопределимых систем по
стадии разрушения дает обычно значительную экономию при проектировании, так как
позволяет дать большую нагрузку на сооружение по сравнению с расчетом по допускаемым напряжениям, исходящим из
предположения об упругой работе системы и принимающим за предельное состояние
такое, при котором система, хотя бы только в одной точке, достигает предела
текучести. Так, в предыдущем примере, если принять коэффициент запаса k=1,67, допускаемая нагрузка Рдоп, определенная из условия разрушения, равна:
Рдоп = ![]() = 4т.
= 4т.
Если же рассчитать эту же систему обычным
способом, при допускаемых напряжениях в стержнях [σ] = ![]() = 1500 кг/см2,
получим для единичной нагрузки
= 1500 кг/см2,
получим для единичной нагрузки
S1=-1,167, S2=0,333, S3=1,833,
и допускаемая нагрузка будет равна:
Рдоп = ![]() = 3,273т.
= 3,273т.
Увеличение несущей способности при
переходе к расчету по разрушающему состоянию составляет 22,2%.
Для каждого
простого и комбинированного механизма разрушения составляют уравнения
равновесия, которые удобнее всего представить в форме уравнения работ [3]
∑Мk,пр θ k = ∑Pi,пр δi , (3)
где θ k – углы поворота стержней
в пластических шарнирах; δi – линейные перемещения точек приложения соответствующих
нагрузок.
Суммирование в уравнении (3) распространяется на все нагрузки
и предельные моменты во всех пластических шарнирах. При этом в уравнениях работ
распределенные нагрузки могут быть заменены их равнодействующими.
Число возможных независимых механизмов разрушения, равное
числу независимых уравнений равновесия статики, определяют по формуле
m = n – л , (4)
где n – число сечений стержней рамы, в которых нужно
найти изгибающие моменты для построения
эпюры изгибающих моментов; л –
степень статической неопределимости рамы.
Возможные
независимые механизмы разрушения могут быть следующих типов: а) балочные (Б);
б) бокового смещения (С); в) рамные (щипцовые) (Щ); г) поворота узлов (У).
Пример. Определить предельные и допустимые нагрузки для
портальной рамы (рисунок 4,a), если Q=1,5Р, предел
текучести стали σт=250МПа
и расчетное сопротивление при изгибе Rи=210МПа,
а пластические моменты сопротивления ригеля и стоек равны соответственно Wр,т =500см3 и Wс,т =250см3.
Построить график предельных сочетаний сил Рпр
и Qпр.
Предельный изгибающий момент для стоек
![]() Н·м = 62,5 кН·м.
Н·м = 62,5 кН·м.
Предельный изгибающий момент для ригеля
![]() Н·м = 125 кН·м.
Н·м = 125 кН·м.
Возможными формами разрушения рамы
являются балочный механизм (Б), показанный на рисунке 4,б, и механизм бокового
смещения (С), изображенный на рисунке 4,в, а также комбинированный механизм
(Б+С), который показан на рисунке 4,г. Для каждого из этих механизмов на основании
принципа возможных перемещений составляем уравнение предельного равновесия в
виде уравнения работ внешних и внутренних сил.
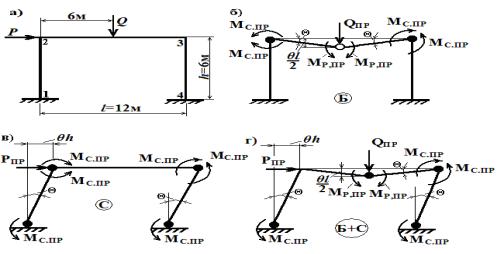
Рисунок 4. Возможные формы
разрушения рамы
Для балочного
механизма (Б)
Qпр (l/2)θ ![]()
откуда
![]() Qпр=4(Мр,пр+Мс,пр)/l=12 Мс,пр /l
Qпр=4(Мр,пр+Мс,пр)/l=12 Мс,пр /l
или
![]() 8Мс,пр /l
8Мс,пр /l
Для
механизма бокового смещения (С)
![]()
откуда
![]()
![]() 8Mc,пр/l.
8Mc,пр/l.
Для
комбинированного механизма (Б+С)
Qпр (l/2)θ +Рпрhθ ![]()
Отсюда,
имея в виду, что h=l/2 и Мр,пр=2Мс,пр,
получим
Qпр +Рпр
= 16Мс,пр /l.
С учетом
того, что, Qпр =1,5Рпр
, имеем
Рпр = 6,4Мс,пр /l=6,4·62,5·103/12 Н =3,33·104Н=33,3кН;
Qпр =1,5Рпр=1,5·33,3=50кН.
Так как
минимальные значения Qпр и Рпр,
являющиеся расчетными, соответствуют комбинированной форме разрушения, то
опасной будет именно эта форма.
Литература
1.
Предельное состояние
элементов железобетонных конструкций. Под ред. д-ра техн. наук проф. С.А.
Дмитриева. Стройиздат. М.-1976-216с.
2.
Аугустин Г., Баратта А.,
Кашпати Ф. Вероятностные методы в строительном проектировании. М. Стройиздат.
1988.-584с.
3.
Кальницкий А.А. Расчет
статически неопределимых железобетонных конструкций с учетом перераспределения
усилий. Стройиздат. М.-1970-168с.
УДК 624.012.35.046
Байнатов Ж.Б., Мурзалина Г.Б.
КазНТУ им.К.И. Сатпаева, Алматы
Вероятностная
оценка механизма разрушения в предельном равновесии
При анализе надежности упругопластических систем
необходимо рассмотреть все механизмы разрушения. Для стержневых систем число
основных механизмов разрушения равно разности между числом пластических
шарниров, образующихся в местах возникновения предельных моментов, и степенью
статической неопределимости системы.
В качестве примера рассмотрим П-образную раму (рис.1)
под действием двухпараметрической нагрузки [1]. Будем считать, что пластические
шарниры могут образовываться в одиннадцати отмеченных на рисунке сечениях.
Далее примем, что положительный и отрицательный предельные
моменты ![]() для каждого сечения равны между собой. Тогда для каждого n-го
возможного пластического шарнира абсолютная величина изгибающего момента Mr должна быть не
больше, чем
для каждого сечения равны между собой. Тогда для каждого n-го
возможного пластического шарнира абсолютная величина изгибающего момента Mr должна быть не
больше, чем ![]() .
.
![]() . (2)
. (2)
Будем считать, что все 11 предельных моментов являются
взаимно независимыми гауссовскими случайными величинами с равными
математическими ожиданиями μMy=10тм и дисперсиями s2My
=(0,1μMy)2. Пусть Pr(My) есть вероятность того, что![]() для любого значения My.
для любого значения My.
Вследствие принятых предпосылок поведение конструкции
«симметрично» относительно знака нагружения, т.е.
![]() (3)
(3)
Следовательно, для расчета конструкции можно
ограничиться первым квадрантом в пространстве нагрузок (W1 ≥ 0;
W2 ≥0).
Сначала используем кинематический подход. Для
усредненной конструкции возможны лишь три механизма разрушения (рис.2).
Пронумеруем их i=1, 2, 3 и запишем для них
диссипацию энергии:
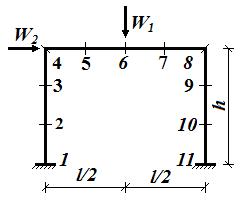
Рис.1. Пример П- образной рамы и места возможных
шарниров;
l = 4,00м, h = 3,00м [1]
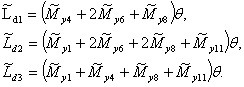 (4)
(4)
Значение угла θ произвольно и будет в дальнейшем
приниматься θ =1.
Поскольку распределение ![]() принято нормальным,
то и
принято нормальным,
то и ![]() распределена
нормально со следующими средними значениями и дисперсиями (там, т2·м2):
распределена
нормально со следующими средними значениями и дисперсиями (там, т2·м2):
![]()
![]()
![]() (5)
(5)
![]()
![]()
![]()
Отсюда легко получаются кинематические
вероятности ![]() для каждого механизма, и легко строятся области
для каждого механизма, и легко строятся области ![]() для любых значений р, например, р=0,1 и р=0,01. Сначала из
таблиц нормального распределения
находим
для любых значений р, например, р=0,1 и р=0,01. Сначала из
таблиц нормального распределения
находим
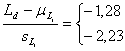 для
для ![]()
![]() (6)
(6)
Затем для каждого из рассматриваемых механизмов находим
р=0,1
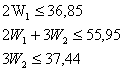
![]() (7)
(7)
р=0,01
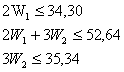
![]() (8)
(8)
Для примера на рис. 2 показаны эпюры моментов Mi
, построенных при двух значениях с=W2/W1.
Вероятность PSi того, что эпюра Mi статически
не допустима определяется (с учетом предпосылки о взаимной независимости
предельных моментов) выражением
![]() (9)
(9) 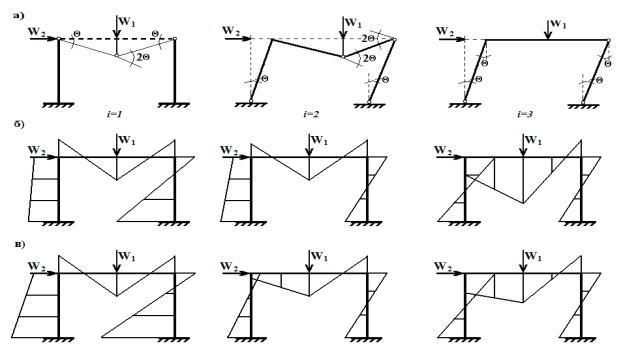
Рисунок 2. П-образная рама:
а – механизмы разрушения осредненной конструкции; б –
эпюры моментов Мi, уравновешивающие внешнюю нагрузку, с=W2/W1=0,8; [1]
Искомые области ![]() определяются как пересечения полупространств (7) или (8). Их
полигональные границы показаны на рис. 3.
определяются как пересечения полупространств (7) или (8). Их
полигональные границы показаны на рис. 3.
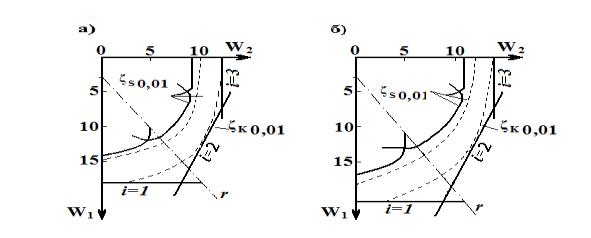
Рис.3. П-образная рама: примеры приближенного
построения областей разрушения а – р=0,01; б – р=0,1 [1]
Рассмотрим теперь случай, когда действующие на ту же
раму (рис. 1) нагрузки изменяются пропорционально одному параметру α.
![]()
Примем W10 = 3т, W1α = 7т, с = 0,5 (рис.4,а). На рис. 3 возможные случаи
нагружения лежат на штрих пунктирной прямой r. При этом механизмов разрушения усредненной
конструкции будет второй (i=2) механизм. Кинематически достаточный параметр
определится формулой (рис. 4,б).
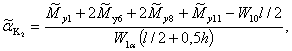 (10)
(10)
откуда
можно получить его среднее значение и дисперсию.
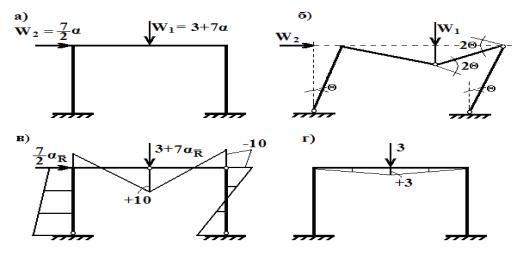
Рис. 4.
П-образная рама под действием однопараметрического нагружения (силы в т,
моменты в т·м) [4]
![]()
![]()
![]() (10)
(10)
Функция
распределения ![]() (α)
(гауссовская) параметра
(α)
(гауссовская) параметра ![]() показана на рис. 5,а, а ее участок малых вероятностей в логарифмическом
масштабе на рис.5,б.
показана на рис. 5,а, а ее участок малых вероятностей в логарифмическом
масштабе на рис.5,б.
Для статического подхода обратимся к эпюре моментов,
приведенной на рис.4,в, которая соответствует предельному равновесию
усредненной конструкции и которую можно получить из эпюры ![]() на рис. 2,б, помня, однако, о том, что постоянная нагрузка W10 должна
уравновешиваться изгибающими моментами, не зависящими от α. Поскольку
конструкция статически неопределима, можно выбрать любую эпюру M0,
уравновешивающую W10. Здесь была использована эпюра, приведенная на
рис.4,г.
на рис. 2,б, помня, однако, о том, что постоянная нагрузка W10 должна
уравновешиваться изгибающими моментами, не зависящими от α. Поскольку
конструкция статически неопределима, можно выбрать любую эпюру M0,
уравновешивающую W10. Здесь была использована эпюра, приведенная на
рис.4,г.
Теперь воспользуемся выражением (9), подставляя в него
вместо Mir
(i=2) следующие значения:
![]() (11)
(11)
Кривая ![]() (α) также показана на рис. 5. Соответствующие ей среднее
значение и дисперсия
(α) также показана на рис. 5. Соответствующие ей среднее
значение и дисперсия
![]()
![]() (12)
(12)
Полученные
результаты позволяют с хорошим приближением получить математическое ожидание
предельного значения ![]() . Действительно из
. Действительно из
![]() = 2,074+0,130,
(13)
= 2,074+0,130,
(13)
что дает возможность
вычислить ![]() с точностью +6,3%.
с точностью +6,3%.
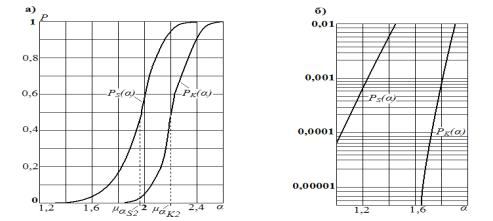
Рисунок 5. Двусторонние оценки функции распределения несущей
способности П-образной рамы при однопараметрическом нагружении [4]
Литература
1.
Предельное состояние
элементов железобетонных конструкций. Под ред. д-ра техн. наук проф. С.А.
Дмитриева. Стройиздат. М.-1976-216с.
2.
Аугустин Г., Баратта А.,
Кашпати Ф. Вероятностные методы в строительном проектировании. М. Стройиздат.
1988.-584с.
3.
Кальницкий А.А. Расчет статически
неопределимых железобетонных конструкций с учетом перераспределения усилий. Стройиздат.
М.-1970-168с.
Конструкции,
принудительно деформирующиеся по высшей форме
Изложенный метод, примененный при анализе работы
модели однопролетного стержня, был
использован В.А. Икриным также и для
анализа модели двухпролетного стержня и П-образной рамы.
На рис.1 показана модель симметричного двухпролетного
стержня, состоящая из четырех абсолютно жестких звеньев, соединенных короткими
податливыми связями 1,2,3 и загруженная продольной сжимающей силой N и двумя поперечными силами βN. Все силы возрастают пропорционально N или ![]() .
.
В начальной стадии нагружения
деформация симметрична. Затем при некотором значении ![]() функциональный опредилитель системы обратится в нуль в
результате обращения в нуль второй производной от полной энергии Т по параметру антисимметричной
деформации γ2. Следовательно, при
функциональный опредилитель системы обратится в нуль в
результате обращения в нуль второй производной от полной энергии Т по параметру антисимметричной
деформации γ2. Следовательно, при ![]() устойчивость симметричной формы деформирования потеряется
из-за появления антисимметричной составляющей деформации.
устойчивость симметричной формы деформирования потеряется
из-за появления антисимметричной составляющей деформации.
Анализ показал, что при
дальнейшем увеличении нагрузки в первой или во второй связи начнется упругая
разгрузка, жесткость системы возрастает и функциональный определитель вновь
станет положительным, из чего следует, что новые состояния равновесия системы
при ![]() будут устойчивыми, а форма ее деформирования смешанная и
содержит как симметричные
будут устойчивыми, а форма ее деформирования смешанная и
содержит как симметричные