Технические науки./12. Автоматизированные системы управления на производстве
К.т.н. Дмитриев А.Г.
Череповецкое высшее
военное инженерное училище радиоэлектроники
Адаптивная
полиномиальная аппроксимация экспериментальных кривых
При решении многих практических задач, например,
при моделировании различных физических процессов, возникает необходимость
аппроксимации экспериментальных кривых, при этом в качестве модели исследуемой
кривой используются многочлены ![]() - ого порядка. При известном
- ого порядка. При известном ![]() построение модели
часто сводится к оценке неизвестных коэффициентов методом наименьших квадратов.
построение модели
часто сводится к оценке неизвестных коэффициентов методом наименьших квадратов.
Задача ставится следующим образом. Пусть для
анализа предъявлена экспериментальная кривая ![]() , причем значения
, причем значения![]() задаются в дискретные моменты времени
задаются в дискретные моменты времени ![]() . Критерий качества аппроксимации
. Критерий качества аппроксимации ![]() на выборке экспериментальных значений
на выборке экспериментальных значений ![]() задается в виде:
задается в виде:
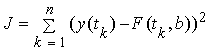 , (1)
, (1)
где
![]() - многочлен степени
- многочлен степени ![]() .
.
Значения оцениваемых параметров ![]() находятся из необходимых
условий минимума критерия (1) и сводятся к вычислению следующего матричного выражения[1]:
находятся из необходимых
условий минимума критерия (1) и сводятся к вычислению следующего матричного выражения[1]:
![]() ,
,
где ![]() - регрессионная матрица размерности
- регрессионная матрица размерности ![]() ,
, ![]() .
.
В работе рассматривается случай, когда порядок
многочлена ![]() заранее неизвестен, ставится задача оценки этого параметра и
последующего построения полиномиальной модели.
заранее неизвестен, ставится задача оценки этого параметра и
последующего построения полиномиальной модели.
Критерий качества аппроксимации ![]() на выборке экспериментальных значений
на выборке экспериментальных значений ![]() выберем в виде:
выберем в виде:
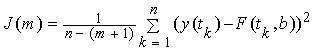 ,
(2)
,
(2)
Требуется найти порядок многочлена ![]() и такие значения вектора оцениваемых параметров
и такие значения вектора оцениваемых параметров ![]() , чтобы критерий (2) имел минимальное значение.
, чтобы критерий (2) имел минимальное значение.
Работа алгоритма состоит в следующем. Для
каждого фиксированного ![]() , начиная с
, начиная с ![]() , определяются значения вектора оцениваемых параметров
, определяются значения вектора оцениваемых параметров ![]() , доставляющие минимум критерию (1), подсчитывается значение
критерия
, доставляющие минимум критерию (1), подсчитывается значение
критерия ![]() . Это значение критерия сравнивается со значением критерия
. Это значение критерия сравнивается со значением критерия ![]() , подсчитанным на предыдущем шаге. Если
, подсчитанным на предыдущем шаге. Если ![]() , то порядок многочлена увеличивается на единицу, т.е.
, то порядок многочлена увеличивается на единицу, т.е. ![]() , определяются значения вектора оцениваемых параметров
, определяются значения вектора оцениваемых параметров ![]() , подсчитывается новое значение критерия
, подсчитывается новое значение критерия![]() , которое сравнивается со значением критерия, подсчитанным на
предыдущем шаге, и т.д.
, которое сравнивается со значением критерия, подсчитанным на
предыдущем шаге, и т.д.
Если на некотором шаге ![]() , то проверяется адекватность моделей порядков
, то проверяется адекватность моделей порядков ![]() и
и ![]() . Для этого подсчитывается статистика
. Для этого подсчитывается статистика
![]() , (3)
, (3)
имеющая
распределение Фишера с 1 и ![]() степенями свободы.
степенями свободы.
Если для
заданного уровня значимости ![]()
![]() , то рассматриваемые модели считаются существенно
различающимися и полученная
аппроксимирующая функция
, то рассматриваемые модели считаются существенно
различающимися и полученная
аппроксимирующая функция ![]() порядка
порядка ![]() считается искомой. В
противном случае порядок модели уменьшается на единицу, т.е.
считается искомой. В
противном случае порядок модели уменьшается на единицу, т.е. ![]() и повторяется проверка адекватности «соседних»
моделей порядков
и повторяется проверка адекватности «соседних»
моделей порядков ![]() и
и ![]() . Такая процедура уменьшения порядка модели продолжается до
тех пор, пока не будет выполняться условие
. Такая процедура уменьшения порядка модели продолжается до
тех пор, пока не будет выполняться условие ![]() . В качестве искомой аппроксимирующей функции выбирается функция
. В качестве искомой аппроксимирующей функции выбирается функция ![]() порядка
порядка ![]() .
.
Разработанный алгоритм был реализован в
математической системе MathCad. Уровень значимости ![]() был выбран равным 0.05.
был выбран равным 0.05.
В результате расчетов получены следующие
значения критерия (2) соответственно для ![]() :
: ![]() . Критерий достиг минимума
при
. Критерий достиг минимума
при ![]() . После завершения работы всей рассмотренной выше процедуры порядок
модели оказался равным 3.
. После завершения работы всей рассмотренной выше процедуры порядок
модели оказался равным 3.
На рисунке
показаны экспериментальные данные и аппроксимирующая функция (![]() ).
).
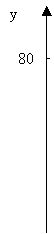
60
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Литература:
1.
Вуколов Э.А. Основы
статистического анализа. – М.: ФОРУМ, 2010. – 464 с.