*119242*

Математика/1. Дифференциальные и интегральные уравнения

К.ф.-м.н. Тингаев А.А.

Одесский институт финансов УГУФМТ, Украина

Регулярные дифференциально-операторные уравнения с запаздыванием

Regular operator-delay-differential equations. This article contains the investigation of conditions on which the systems of the operator-delay-differential equations have solutions that satisfy to the set estimation. The sufficient conditions of existence of such solutions are obtained.

Регулярные дифференциально-операторные уравнения с запаздыванием. Изучается проблема существования решений систем дифференциально-операторных уравнений с запаздыванием, удовлетворяющих заданной оценке. Получены достаточные условия существования таких решений.

Постановка задачи. Изучение асимптотических свойств решений дифференциальных уравнений и систем с обычным аргументом и аргументом с запаздыванием принадлежит к наиболее актуальным задачам качественной теории дифференциальных уравнений, к которым, как известно, сводятся математические модели механики, электротехники, атомной и ядерной физики, физхимии, математической биологии и др. Направления исследований таких уравнений и их систем достаточно разнообразны, однако общей теории пока не существует. Поэтому каждая новая задача и каждая новая ее модификация актуальна и требует собственных, не традиционных подходов и доказательств фундаментальных теорем.

Анализ последних достижений. Теория дифференциальных уравнений с запаздыванием в достаточно полном виде появилась во второй половине пришлого века (см., например, [1] ,[2]). Актуальность практических применений повлияла на появление функционально-дифференциальных уравнений, которые исследуются по нынешнее время ([6], [7] ). Операторы Вольтера были в уравнениях с запаздыванием почти с самого начала развития теории. Сейчас речь идет уже про свойства дифференциально-операторных уравнений с запаздыванием, которые содержат в себе операторы других видов.

Цель статьи. Провести изучение вопроса о существовании решений систем дифференциально-операторных уравнений с запаздыванием, удовлетворяющих заданной оценке. Получить достаточные условия существования таких решений. Такая задача для данных систем поставлена впервые.

Изложение основного материала. Рассмотрим систему уравнений вида

(1)

где ,

Решения системы (1) ищутся в полном нормированном пространстве Х векторных функций , в котором

a) , где , (2а)

b) . (2b)

В пространстве Х введем норму следующим образом:

Нетрудно доказать, что Х — полное пространство.

Далее, в пространстве Х введем в рассмотрение класс функций

(3)

Очевидно, что множество является выпуклым, ограниченным и замкнутым.

Под символами A, b, f будем понимать операторы, отображающие векторные функции соответственно в функции

,

,

.

Здесь под понимается

.

В качестве области изменения (x, y) рассматривается область

. (4)

где

на . (5)

Величина d₀ подбирается в зависимости от свойств A, b, f и поэтому увеличивать ее, вообще говоря, нельзя.

Ставится задача: выяснить, при каких условиях на , , существует решение системы (1) из B.

Из вида области и условия (5) следует, что, если , то . Поэтому может идти речь о поведении элементов матрицы и компонентов векторов , при . Из того, что в точке x = 0 они, вообще говоря, не определены, следует, что элементы матрицы и компоненты векторов , могут иметь в точке O(0;0) особенность, причем каждая из них — свою. То есть, при они могут не иметь предела, могут не сохранять знак, могут быть неограниченными и, в частности, некоторые из них могут тождественно равняться нулю.

Основные предположения и построения

Лемма 1. Пусть B₀ — бесконечное множество пространства X, такое, что:

a) ;

b) Существуют положительные постоянные d₀ и K, такие, что :

, .

Тогда B₀ относительно компактно в X.

Учитывая определение нормы (2), условия b) Леммы запишутся так:

.

Определение. Говорят, что функция имеет производные в силу системы

, (6)

если

,

,

и так далее. Название объясняется формулой

, ,

где у(х) — произвольное решение уравнения (6).

Определение (условие типа условия Липшица)

Будем говорить, что функция , где , , удовлетворяет условию типа условия Липшица по всем переменным, кроме x, в области , если , и любых двух точек , , как только , где (0 < h, a_k — const) и на (0;D], , то существуют такие непрерывные положительные на (0;D] функции L_k(x) () и L⁰(x), что будет справедливо неравенство:

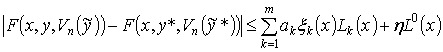
и обозначается так: . Здесь  . Функции L(x) и L⁰(x) будем называть функциями Липшица.

Замечание. Чтобы избежать громоздкости обозначений, в дальнейшем под L(x) будем понимать L(x, x, c₀), указывая область изменения (х;у).

Метод решения поставленной задачи и вспомогательные построения

Существование решения системы (1), стремящегося к нулю при x® +0 вместе со своими производными до п-го порядка включительно, докажем с помощью принципа неподвижной точки Шаудера относительно класса В в полном нормированном пространстве X.

Для этого зададим на множестве В оператор А таким образом, чтобы его неподвижная точка была решением системы (1). А именно:

каждой функции поставим в соответствие векторную функцию — решение системы

()

Затем определим достаточные условия того, что оператор А удовлетворяет таким условиям:

I. А определен и однозначен в В.

II. А отображает В в себя.

III. Множество А(В) является относительно компактным в В.

IV. А — непрерывный в В.

Система () в точке х = 0 не удовлетворяет условиям теоремы Пикара-Коши. Поэтому при изучении данной системы и решении поставленной задачи применим качественный метод: исследование поведения интегральных кривых с помощью кусочно-гладких или гладких поверхностей без контакта, а также топологического принципа Важевского.

Существование и асимптотическая оценка решений системы вблизи особой точки

Рассмотрим систему частного вида:

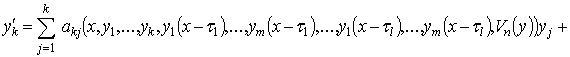
(8)

, a_kj º 0 "j > k

и на классе B зададим оператор A указанным выше способом. Тогда "Î В соответствующая система () имеет вид

()

.

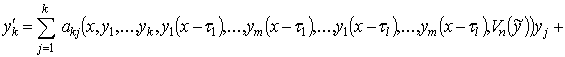
Введем в рассмотрение области

D_k(D, dj) = {(x, y_l,...,y_k): xÎ(0;D];½ y_j½ £ d_jj_j (x), }, ,

где j_j Î C¹[0;D], j_j(0) = 0, j_j(x), j'_j(x) > 0 на (0;D], ,

j_j(x) = o(c_j(x)) при x ® +0, 0 < d_j = const.,

и предположим, что для каждого фиксированного значения d_k величина D подбирается достаточно малой так, что

D_k(D,dj) Ì D_k(D,(d+e₀)j) Ì D_k(D,c), (0 < e₀ = const), .

Обозначим w_k(j) =

=  –, .

Обозначим последовательные производные правой части этой системы в силу системы () через

= , (9)

т.е. положим

= [

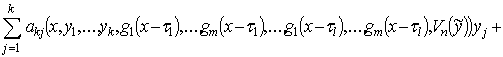
]^{(p – 1)}

, .

Из вида (9) следует предположение, что последовательное n‑кратное дифференцирование в силу системы () не повышает наивысшего порядка входящих в них производных.

Если, в частности, система () — интегро-дифференциальная, то это означает, что функция, содержащая ^(p)(х) (), стоит под знаком не менее, чем р‑кратного интеграла. То есть, производные как бы "погашаются" интегрированием, поэтому такую систему нельзя считать системой п‑го порядка.

Теорема. Пусть "Î В соответствующая система () удовлетворяет следующим условиям:

1°. Существует такая вектор-функция j Î R^m, что " в области D_k(D, (d+e₀)j) выражения w_k(j_k) сохраняют знак и среди них есть хотя бы два противоположного знака.

2°. Если w_k(j_k) < 0, то предположим, что существует функция y_k(x), где

a. y_k(x) Î С¹[0;D], y_k(0) = 0, y_k(x), y'_k(x) > 0 на (0;D].

b. j_k(x) = o(y_k(x)), y_k(x) = o(c_k(x)) при х ® +0 такая, что соответствующее выражение w_k(y_k) < 0 в области

D_k(D, (d + e₀ + С⁰) y_k), 0 < С⁰ = const

3°. a. , , (x, y) Î С (D_k(D,c)), ,

( р = 1 при n = 0 и р = n при n ³ 1).

b. f_k(x,y_l,...,y_k,V_n()) = o(j_k (x)w_k(j_k)) при х ® +0;

, (x,y_l,...,y_k) Î D_k(D, (d+e₀)j)

4°. "(x,y_l,...,y_k) Î D_k(D,(d+e₀)j) существуют положительные постоянные m_k, m_kj такие, что

a. 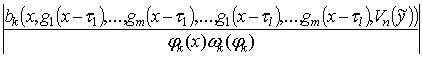£ m_k, ;

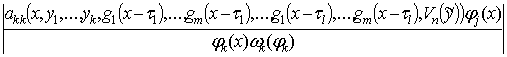b. £m_kj,

, ;

5°. a. a_kj Î Typ Lip_{у1 … уkVп}(D_k(D,dj); L_kj1(x),… , L_kjk(x), L⁰_kj (x)); , ;

b. b_k Î Typ Lip_Vп(D_k(D,dj); L⁰_k(x)); ;

c. f_k Î Typ Lip_{у1 … уkVп}(D_k(D,dj);L¹_k1(x),…,L¹_kk(x),L^0,1_kj(x)); ;

Причем соответствующие функции Липшица должны удовлетворять условиям:

a₁. L_kjk(x) = o(j_j^–1(x)w_k(y_k)) при х ® +0, , ;

(x,y_l,...,y_k) ΠD_k(D,(d + e₀ + С⁰)y_k);

a₂. L_kji(x) = o(j_k(x)j_j^–1(x)j_i^–1(x)w_k(j_k))

при х ® +0, , i,; (x,y_l,...,y_k) ΠD_k(D,(d + e₀)j);

a₃. (x) = O(j_k(x)j_j^–1(x)w_k(j_k)); , ;

(x,y_l,...,y_k) ΠD_k(D,(d + e₀)j);

b₁. (x) = O(j_k(x)w_k(j_k)); (x,y_l,...,y_k) ΠD_k(D,(d + e₀)j); ;

c₁. (x) = o(w_k(y_k)) при х ® +0, ;

(x,y_l,...,y_k) ΠD_k(D,(d + e₀ + С⁰)y_k);

c₂. (x) = o(j_k(x)j_i^–1(x)w_k(j_k)) при х ® +0, , ;

(x,y_l,...,y_k) ΠD_k(D,(d + e₀)j);

c₃. (x) = O(j_k(x)w_k(j_k)); (x,y_l,...,y_k) ΠD_k(D,(d + e₀)j); ;

6°. a. Î Typ Lip_{у1 … уkVп}(D_k(D,(d +e₀)j); L_kp1(x),…,L_kpk(x),L⁰_kp);

, ; причем

L_kpi(x) = O(j_i^–1(x)), , ; 0 < L⁰_kp = const

b. = o(1) при х ® +0, , ,

(x,y_l,...,y_k) ΠD_k(D,dj);

c. = O(1) , (x,y_l,...,y_k) ΠD_k(D,dj).

Тогда система (8) на [0;D'] ( D' — достаточно малое положительное число), имеет не менее, чем r‑параметрическое семейство решений {y_0k(x)} из класса B, где r — число положительных w_k(j_k) (1 £ r < m). Причем решения { y_0k(x)} на [0;D'] удовлетворяют следующим условиям:

1) £ d_kj_k(x), ;

2) y= O(1) .

Замечание. Вид функции j(x), вообще говоря, может зависеть от начальной функции g на E₀ = [–t;0], то есть при одном и том же уравнении для разных начальных функций оценки решений могут быть различны.

Доказательство теоремы

Из вида системы () следует, что ее можно исследовать, рассматривая последовательно каждое уравнение отдельно; поэтому доказательство ведется шаг за шагом, причем на каждом шаге докажем, что "Î В и ":

I_k. (A)_k однозначно определен в В.

II_k. £ d₀, .

III_k (A)(x) — ограничено.

IV_k. (A)_k — непрерывный в В.

Пусть k = 1. Тогда соответствующее уравнение имеет вид

(₁)

Изучим поведение решений уравнения (₁) на поверхности

= (x), x Î (0;D] (9₁)

(где d₁ — пока не определено).

Обозначим через вектор внешней нормали к поверхности (9₁) в произвольной точке, а через — вектор поля направлений, определяемого уравнением (₁), в той же точке. Тогда, так как

= (y₁, – j₁(x) j'₁(x)), = (у'₁, 1),

то получаем

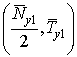= (x)w₁(j₁) ´

´{ 1 +  +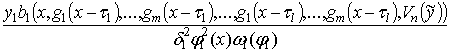

+ }.

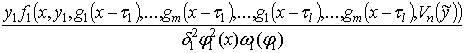Сделаем необходимые оценки на поверхности (9₁). Учитывая (4°.а), (3°.b), при k = 1 имеем:

£ ,

£

£ .

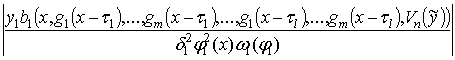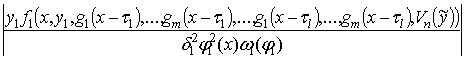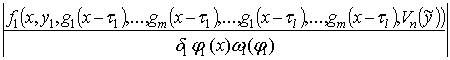Теперь число d₁ > 0 подбирается настолько большим, чтобы £ и зафиксируем его. А постоянная величина D > 0 подбирается настолько малой, чтобы выполнялись условия

(x) < c₁(x), £ .

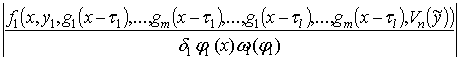Это возможно в силу условия (3°.b).

В силу (3°.а) в области, ограниченной поверхностью (9₁) условия теоремы Пикара-Коши выполнены и поэтому через каждую точку области проходит единственная интегральная кривая. Кроме того, в силу сделанных оценок на поверхности (9₁), имеем:

sign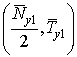 = sign (w₁(j₁)) = ± 1.

I₁. Покажем, что образ (A)₁ однозначно определен в В.

Пусть сначала

1) w₁(j₁) > 0 на поверхности (9₁). Тогда sign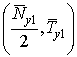 = +1, и, следовательно, все точки поверхности (9₁) на (0, D] при убывании х являются точками строгого входа для уравнения (₁). Чтобы зафиксировать единственный образ (A)₁ , потребуем выполнение начального условия:

(A)₁(D) = , = C, (10₁)

где £ d₁j₁(D).

Тогда каждому значению будет соответствовать единственный образ (A)₁ продолжаемый на (0;D]. Образ (A)₁ окажется зависящим от параметра , то есть получим однопараметрическое семейство операторов (A)_1C, однозначно определённых на (0;D] и таких, что

£ d₁j₁(x). (11₁)

2) Пусть далее w₁(j₁) < 0 на поверхности (9₁). Тогда sign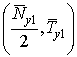= –1 и, следовательно, поверхность (9₁) является поверхностью точек строгого выхода при убывании х. В силу топологического принципа Важевского, на отрезке S₁ = {x = D; |y₁| £ d₁j₁(D)} существует хотя бы одна точка, которой соответствует решение уравнения (₁), определенное на (0;D] и удовлетворяющее условию (11₁). Обозначим его через (A)₁. Покажем, что такое решение единственно. Для этого в (₁) положим:

y₁(x) = (A)₁(x) + Z₁(x).

Тогда относительно Z₁(x) получим уравнение

(x) = a₁₁(x, (A)₁+Z₁,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n())Z₁+

+ [a₁₁(x,(A)₁+Z₁,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n()) –

– a₁₁(x,(A)₁,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n())](A)₁+ (12₁)

+ [f₁(x,(A)₁+Z₁,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n()) –

– f₁(x,(A)₁,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n())].

Очевидно, Z₁ = 0 является решением уравнения (12₁). Покажем, что уравнение (12₁) не имеет других решений, стремящихся к нулю, как j₁(x) при x ® +0. По аналогии с предыдущим, для исследования интегральных кривых уравнения (12₁) применим качественный метод.

Введем в рассмотрение однопараметрическое семейство поверхностей

= (x), x Î (0;D] (13₁)

где C₁ — параметр, 0 < С₁ < .

Очевидно, что D_z1(D,y₁) Ì D₁(D,c₁) (это следует из (2°.b) при k = 1), поэтому через каждую точку области, ограниченной поверхностью (13₁), проходит единственная непрерывная интегральная кривая.

Обозначим через — вектор внешней нормали к поверхности (13₁) в произвольной точке, а через — вектор поля, определяемого уравнением (12₁) в той же точке. Тогда

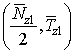 = (x)w₁(y₁)´{1+

+  –

–  +

+  –

– }.

Сделаем необходимые оценки на поверхности (13₁). В силу условий а) и с) из (5°) теоремы при k = 1 имеем

1. £

£ = .

2. £

£

В силу условий (5°.a₁), (5°.c₁) и (2°.b) существует D₁₀ Î (0;D], такое что "x Î (0;D]:

£ (14₁)

£ (15₁)

d₁j₁(x) + Cy₁(x) < c₁(x) . (16₁)

В результате, равномерно для всех С₁ Î ( 0;C] на (0;D₁₀]:

sign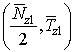 = sign w₁(y₁) = –1.

Это значит, что при убывании х все точки на поверхности (13₁) являются точками строгого выхода. Значит, если бы существовало хотя бы одно нетривиальное решение уравнения (12₁), стремящееся к нулю как j₁(x), то, в силу (2°.b), при k = 1 соответствующая интегральная кривая пересекла бы одну из кривых семейства (13₁) в направлении входа, это невозможно, в силу единственности интегральной кривой, проходящей через произвольную фиксированную точку области, ограниченной поверхностью (13₁).

Значит, нетривиальных решений уравнения (12₁), имеющих порядок j₁(x) — нет. Отсюда следует, что уравнение (₁) имеет единственное решение (A)₁ , удовлетворяющее при x Î (0, D] оценке (11₁).

В результате доказано, что "Î В существует единственный образ (A)₁. То есть образ (A)₁ однозначно определен на В.

II₁. Докажем, что "Î В:

£ d₀ , . (17₁)

По доказанному на (0;D]: £ d₁j₁(x) .

Отсюда, так как j₁(0) = 0, всегда можно выбрать значение D Π(0;D] настолько малым, чтобы на (0;D] было d₁j₁(x) £ d₁. И поэтому выполняется неравенство (17₁) при p = 0.

Так как по построению "x Î (0, D₀]: £ d₁j₁(x), то, в силу условия (6°.b), при, достаточно малом DΠ(0;D]:

=

= £ d₀

"x Î (0;D], .

Значит, £ d₀ , .

Из (11₁) и условия (5°.b) вытекает, что

(Ay)(x) = 0, x Î (0, D], ".

Доопределим (A)(x) в точке х = 0 и положим (A)(0) = 0.

Обозначим D = D. Тогда (A)₁ Î C ⁿ[0, D].

III₁. Докажем, что "Î В $Р₁ = const, Р₁ > 0 такое, что

£ Р₁.

Заметим, что из II₁ следует, что "Î В: (A)₁ … (A) — равномерно ограничены на [0, D]. По условию (6°.с) теоремы существует положительная постоянная P₁₀ такая, что "Î В

£ P₁₀

Значит, множество (A)₁ удовлетворяет оценке

½½ ((A)₁)¢½½ £ Р₁ £ max [P₁₀, d₀ ]

и потому оно относительно компактно в В.

IV₁. Докажем непрерывность образа (A)₁ в В.

Требуется доказать, что "e > 0 $h(e) > 0, что ", *Î В, ½½ – *½½ < h, следует < e, .

Положим в уравнении (₁)

(A)₁ = (A*)₁ + q₁,

причём считаем , *, (A*)₁ — известными, а (A)₁ — неизвестной, то есть q₁ — неизвестная.

Тогда относительно q₁ на [0;D] получим следующее уравнение:

q₁'(x) =  a₁₁(x,(A*)₁+q₁,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n())q₁ +

+ [a₁₁(x,(A*)₁+q₁,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n()) –

– a₁₁(x,(A*)₁,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n(*))](A*)₁+

+ [b₁(x ,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n()) – (18₁)

– b₁(x, g₁(x – t₁),…, g_m(x – t₁),…, g₁(x – t_l),…, g_m(x – t_l), V_n(*))] +

+ [f₁(x, (A*)₁+ q₁ , g₁(x – t₁),…, g_m(x – t₁),…, g₁(x – t_l),…, g_m(x – t_l), V_n()) –

– f₁(x, (A*)₁, g₁(x – t₁),…, g_m(x – t₁),…, g₁(x – t_l),…, g_m(x – t_l), V_n(*))].

Зададим произвольное значение e Î (0;e₀) (0 < e₀) и будем искать соответствующее h(e). Для этого рассмотрим область

D_k(D,ed₁j₁) = {(x, q₁): xÎ(0;D₁];½ q₁(x)½ £ ed₁j₁(x)},

Изучим поведение решений уравнения (18₁) на поверхности

q (x) £ e²dj(x), x Î (0;D]. (19₁)

Сохраняя прежние обозначения, имеем:

= e²dj(x)w₁(j₁)´{1 +

+ –

– +

+ –

–

+ –

– }.

Сделаем необходимые оценки на поверхности (19₁). Учитывая условия (5°.a,b,c) при k = 1 имеем:

1. £

£ [ed₁j₁(x)L₁₁₁(x) + hL⁰₁₁(x)] = + .

2. £ .

3. £

£ + .

Далее, в силу (2°.b), (5°.а₂) (5°.с₂), всегда можно уменьшить D > 0 так, что на промежутке (0;D]:

a) (1 + e₀) d₁j₁ < c₁(x)

b) ½ ½ £ , ½ ½ £ .

В силу (5°.a₃,b₁,c₃) существуют положительные постоянные h₁₁, h, h₁ такие, что "x Î (0;D]:

½ ½ £ h₁₁, £ h, £ h₁ .

Теперь выберем значение h(e) так, чтобы (h₁₁ + h + h₁) £ .

В итоге на (0;D]: sign = sign w₁(j₁) = ±1.

Пусть сначала

1) w₁(j₁) > 0 на поверхности (19₁).

Тогда sign = +1 и, следовательно, поверхность (19₁) — поверхность точек строгого входа для уравнения (18₁) при x ® +0. Это означает, по построению, что уравнение (18₁) имеет единственное решение q(x), удовлетворяющее условиям

q (D) = 0

£ ed₁j(x) (20₁)

Теперь пусть

2) w₁(j₁) < 0 на поверхности (19₁).

Тогда sign  = 1 и, следовательно, поверхность (19₁) — поверхность точек строгого выхода при x ® +0. Продолжая действовать по аналогии с I₁.2, на основании принципа Важевского доказывается существование в области D_q1(D,d₁e₀j₁), по крайней мере, одного непрерывного решения уравнения (18₁), обозначим его через q (x), удовлетворяющего условию (20₁).

Покажем, что такое решение единственное. Для этого положим в (18₁):

q₁ (x) = q (x) + n₁(x).

Тогда относительно n₁(x) получим уравнение:

n₁'(x) = a₁₁(x,(A*)₁+q +n₁,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n())n₁+

+((A*)₁+q)´[a₁₁(x, (A*)₁+q+n₁ ,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n()) –

– a₁₁(x,(A*)₁ +q, g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n())]+ (21₁)

+ [f₁(x, (A*)₁ + q + n₁, g₁(x – t₁),…, g_m(x – t₁),…, g₁(x – t_l),…, g_m(x – t_l), V_n()) –

– f₁(x, (A*)₁ + q, g₁(x – t₁),…, g_m(x – t₁),…, g₁(x – t_l),…, g_m(x – t_l), V_n())].

Изучим поведение решений уравнения (21₁) на семействе поверхностей

n(x) = d(x)y(x), x Î (0, D] (22₁)

где d₁ — параметр, 0 < d₁ < d .

Чтобы не выйти из области определения функций, будем считать D > 0 подобранным так, чтобы на (0;D]

d₁j(x) + e₀d₁j(x) + d₁y₁(x) < c₁(x).

Это возможно в силу (2°.b).

Рассмотрим

= dy(x)w₁(y₁)´{1 +

+ +

+ – (23₁)

– }

В силу условий (5°.а) и (5°.с) и оценок (14₁) и (15₁), оценки слагаемых в выражении (23₁) на поверхности (22₁) будут иметь вид:

1. £

£ £ . (24₁)

2. £

£ £ . (25₁)

В результате оценок (24₁) и (25₁) на (0;D]:

sign = sign w₁(y₁) = – 1 равномерно относительно d₁Î (0;d].

Рассуждая аналогично предыдущему, приходим к выводу, что единственным решением порядка O(j₁) при x ® +0 является тривиальное решение.

Значит, уравнение (18₁) имеет единственное решение q(x), удовлетворяющее оценке (20₁). Тогда получаем, что соответствующее Î В уравнение (₁) имеет решение y(x) = q₀(x) + (A*)₁(x), которое на (0;D] удовлетворяет оценке

£ (e₀ +1) d₁j₁(x).

Но ранее было доказано (см. I₁), что уравнение (₁) имеет единственное решение (A)₁(x), стремящееся к нулю при x ® +0, как j₁(x). Значит, в силу единственности, (A)₁ = q(x) + (A*)₁(x) и поэтому

£ ed₁ j₁(x), x Î (0, D].

Итак, доказано, что "e > 0 $h(e) > 0, что ",*Î В (таких, что выполнено неравенство ½½ – *½½ < h) следует

= £ ed₁j₁(x) £ ed₁j₁(D) = eH.

Покажем, что

< e ". (26₁)

Так как q(x) = (A)₁ – (A*)₁, то

q(x) = Ф(x,(A*)₁+q,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n())–

– Ф(x,(A)₁,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…,g_m(x – t_l),V_n(*)), . (27₁)

Пользуясь условием (6°.а) и равенством (27₁) получим, что

£ ed₁j₁(x)L_11p(x) + Lh £ e×(d₁j₁(x)L_11p(x) + ).

В силу условия (6°.а) существуют положительные константы q, такие, что "x Î(0;D]:

j₁(x)L_11p(x) £ q.

Тогда £ e H , где H = d₁ q + .

Обозначим H₁ = H . Теперь в качестве e берем . Тогда (26₁) будет доказано.

Итак, (A)₁ построен, и на достаточно малом [0;D] обладает следующими свойствами

a) (A)₁ ÎCⁿ[0;D]

b) £ d₁j₁(x)

с) (A)(0) = 0,

d) (A)(0) = O(1), x Î [0;D]

Далее воспользуемся методом математической индукции.

Предположим, что построены (A)₁, … , (A)_k–1 (), обладающие аналогичными свойствами, т. е. ", "x Î [0;D]:

a) (A)_j ÎCⁿ[0;D]

b) £ d_jj_j(x)

с) (A)(0) = 0, (28)

d) (A)(0) = O(1), x Î [0;D]

Тогда относительно (A)_k получим уравнение:

y =  a_kj(x,(A)₁,...,(A)_k–1, y_k,g₁(x – t₁),…,g_m(x – t₁),…,g₁(x – t_l),…

…,g_m(x – t_l),V_n())(A)_j +

+ a_kk(x, (A)₁,..., (A)_k–1, y_k, g₁(x – t₁),…, g_m(x – t₁),…, g₁(x – t_l),…, g_m(x – t_l), V_n())y_k +

+ b_k(x, g₁(x – t₁),…, g_m(x – t₁),…, g₁(x – t_l),…, g_m(x – t_l), V_n())+

+ f_k(x, (A)₁,..., (A)_k–1, y_k, g₁(x – t₁),…, g_m(x – t₁),…, g₁(x – t_l),…, g_m(x – t_l), V_n()).

Остается доказать, что на достаточно малом промежутке [0;D] образ (A)_k  определен и обладает свойствами (28). Тогда в силу произвольности выбора k, это будет означать, что A = ((A)₁, … , (A)_m) — построен и обладает необходимыми свойствами.

Пусть . Тогда соответствующее уравнение имеет вид

у = a_kj(x, (A)₁,..., (A)_k–1, y_k, g₁(x – t₁),…, g_m(x – t₁),…, g₁(x – t_l),…, g_m(x – t_l), V_n())y₁ +

+ a_kk(x, (A)₁,..., (A)_k–1, y_k, g₁(x – t₁),…, g_m(x – t₁),…, g₁(x – t_l),…, g_m(x – t_l), V_n())y_k +

+ b_k(x, g₁(x – t₁),…, g_m(x – t₁),…, g₁(x – t_l),…, g_m(x – t_l), V_n())+ (_k)

+ f_k(x, (A)₁,..., (A)_k–1, y_k, g₁(x – t₁),…, g_m(x – t₁),…, g₁(x – t_l),…, g_m(x – t_l), V_n()).

Рассуждая аналогично предыдущему, легко получить, что для каждого из образов (A)_k () условия (28) выполнены и, следовательно, оператор A в B удовлетворяет условиям принципа Шаудера.

Это означает, что на множестве A(B) существует хотя бы один элемент у₀(x) Î В такой, что y_0k|_{Eo = [–t;0]} = g_k(x), , и на отрезке [0;D¢] выполняются оценки

a. (x, y₀) Î D(D, dj)

b. у(x) = O(1).

Число таких решений зависит не менее, чем от r параметров, где r — число положительных w_k(j_k) (), причем 1 £ r < m. Теорема доказана.

Литература

1. Bellman R. and Cooke K.L. Differential-Difference Equations. NY–London.-1963, Acad. Press

2. Wazewski T. Sur une principe topologique de l'examen asymptotique des integrales des equations differentielles//Ann. Soc. Polon. Math. - 1947. - Vol. 20, №8.- Р. 279-313.

3. Хартман Ф. Обыкновенные дифференциальные уравнения: Пер. с англ. - М.: Мир, 1970. - 720 с.

4. Кигурадзе И. Т. Некоторые сингулярные краевые задачи для обыкновенных дифференциальных уравнений. - Тбилиси: Изд. Тбил. ун-та, 1975. – 352 с.

5. Мышкис А. Д., Эльсгольц Л. Э. Состояние и проблемы теории дифференциальных уравнений с отклоняющимся аргументом. М.- УМН, 22:2(134) (1967), с. 21–57

6. Андреев А. С.  Метод функционалов Ляпунова в задаче об устойчивости функционально-дифференциальных уравнений. «Автомат. и телемех.», 2009, № 9, с. 4–55

7. Власов В. , Медведев  Д. А. , “Функционально-дифференциальные уравнения в пространствах Соболева и связанные с ними вопросы спектральной теории”, Функционально-дифференциальные уравнения, СМФН, 30, РУДН, М., 2008, с. 3–173

8. Грабовская Р. Г., Тингаев А. А. Асимптотические оценки решений некоторых сингулярных дифференциально-операторных уравнений // Международная конференция "Ляпуновские чтения". Тезисы докладов. - Харьков - 1992. - С. 35-36.

9. Джабер А. Ш. М. Сингулярні диференціально-операторні системи рівнянь першого порядку: Автореф. дис. канд. фіз.-мат. наук: 01.01.02./ Одес. Держ. ун-т - Од., 1998. - 16 с.

10. Грабовская Р.Г., Муса Абу Эль-Шаур. Сингулярные дифференциально-операторные системы уравнений частого вида // Математика и психология в педагогической системе “Технический университет”: Сб. ст. 1-й Междунар. науч.-практич. конф.-Ч.2.- Одесса: ОГПУ, 1996. с. 23-25.