*119691*

Закинян Р.Г., Редькина Т.В.

ФГАОУ ВПО «Северо-Кавказский федеральный университет»

Преобразования Бэклунда для нелинейных уравнений

с гиперболической линейной частью

В статье исследуются уравнения на функции двух независимых переменных, встречающиеся в различных задачах гидродинамики и физики атмосферы, связанные с тепловой конвекцией. В частности такие уравнения встречаются в задаче Бенара – Релея и в модели Лоренца. Для них рассмотрена возможность построения преобразований Бэклунда и дальнейшее использование этих преобразований для получения точных решений.

Для построения преобразований Бэклунда использовался метод Клэрэна [1].

Утверждение 1. Два уравнения в частных производных:

(1)

и (2)

где - функции двух переменных, - произвольные функции одной переменной, связаны преобразованием Беклунда вида:

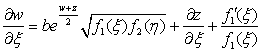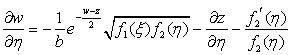, , (3)

b - произвольный параметр.

Доказательство сводится к перекрестному дифференцированию равенств (3) и сложению или вычитанию полученных выражений.

Утверждение 2. Если уравнение (1) имеет решение

, (4)

то уравнение (2) имеет решение

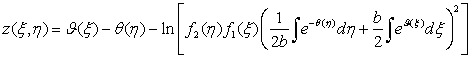, (5)

где - произвольные функции.

Доказательство. Выполнив подстановку решения (4) в преобразования Беклунда (3) и замену получим два уравнения Бернулли, решения которых имеют вид

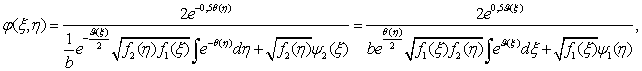
где - постоянные интегрирования. Доопределяя эти функции таким образом, чтобы равенство выполнялось, получим решение (5), подобное которому для некоторых специальных случаев было найдено в работе [2].

Рассмотрим нелинейное гиперболическое уравнение

, (6)

где - неизвестная функция.

Утверждение 3. Преобразования Беклунда вида:

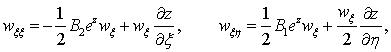(7)

связывают два уравнения: уравнение (6) и нелинейное уравнение

, (8)

где - неизвестная функция двух переменных.

Доказательство проводится аналогично утверждению 1.

Утверждение 4. Если уравнение (8) имеет решение

, (9)

то уравнение (6) имеет решение

(10)

Доказательство. Воспользуемся найденными преобразованиями (7) и подставим известное решение (9), тогда система примет вид

(11)

откуда из первого линейного уравнения в частных произвольных находим связь между независимыми переменными : , где - произвольная функция, вид которой определяем из второго уравнения системы (11): В результате найдено решение уравнения (6) в виде (10).

Утверждение 5. Если уравнение (8) имеет решение

(12)

то уравнение (6) имеет решение

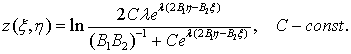(13)

Построение решения осуществляется аналогично утверждению 4.

Преобразования (7) можно использовать и для определения решений уравнения (8).

Утверждение 6. Если уравнение (6), имеет решение

, (14)

то уравнение (8) имеет решение

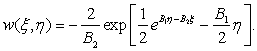(15)

Доказательство. Используя преобразования (7), подставим имеющееся решение (14), тогда получим систему, которую можно проинтегрировать

(16)

где , - постоянные интегрирования. Доопределим функции и так, чтобы полученные значения правых частей системы (16) совпали, это возможно, если В результате определилось значение , тогда 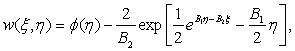где - произвольная функция. Для уточнения выполним проверку. Равенство (8) будет выполняться тождественно, если: . Полученное уравнение на функцию зависит от переменной , чего быть не должно, следовательно, необходимо положить . В результате искомая функция имеет вид (15).

Литература

1. Лэм Дж. Л. Введение в теорию солитонов. – М.: Мир, 1983. – 294 с.

2. Сабитов И.Х. О решениях уравнения в некоторых специальных случаях. //Математический сборник. – Т. 192, № 6. – С. 89 – 104.