*120051*

Dokukova N.A., Kaftaikina E.N.

Belarusian state university, Belarus

The synchronization of two linear oscillators

 

The synchronization of the oscillatory systems is one of the actual problems of modern electronics and physics, many areas of natural, engineering and social sciences, medicine, biomechanics, and astrophysics. This phenomenon is used for the satellites orientation in space. Schumann waves with a fundamental frequency of 7.8 Hz with a 24-hour harmonic effect on the circadian rhythm of the human body and the autonomic nervous system. Cells are synchronously dividing in the early stages of embryonic development, cardiac muscle fibers are reduced synchronously also. It is observed in flight of birds flocks and movement of fish stocks: flapping wings and fins occur simultaneously. The phenomenon of oscillation synchronization with external radio weakest signal is the basis of receiving radios. The first researcher who observed this phenomenon and the basic tenets of the synchronization was the Dutch scientist Christiaan Huygens [1, 2].

The following statement can be found at the scientific literature as definition of the synchronization: it is the rhythms adjustment of the oscillating systems due to the weak interaction between them The explanation of this process has been very difficult and is currently pending. Mechanisms of certain features manifestation is not entirely clear in this phenomenon, for example the mutual vibrations of oscillating systems. Some of them have the different nature, such as watches, lasers, generators, electronic, biological matter. First synchronization phenomenon in acoustic and electroacoustic systems found Rayleigh. The first mathematical model synchronization excitations heart was proposed by Van der Pol. Recently, much attention is paid to the study of synchronization in physiological systems.

In modern conditions, the term "synchronization" refers to a variety of phenomena that occur in almost all areas of science, technology and social life, events that seem quite different, but, nevertheless, subject to universal laws. Synchronization can be identical, in which there is a complete overlap of the amplitude, phase and frequency, can be manifested in a certain ratio between the phases and frequencies of oscillation systems, with the amplitude of systems oscillations may be different, in which case it is called a phase or frequency.

The paper lists the main tenets of synchronization in mechanical systems, a common linear dynamical model of the physical phenomenon consisting in the vibrations of the two autonomous oscillators with a common bond is represented, the motion equation is written, the features and patterns are investigated at the presented mathematical models to study the behavior of objects with a corresponding change in the parameters, analytical formulas for the vibrational modes of all bodies are obtained in a dynamic system, using the method developed by the authors in [3, 4], the numerical and analytical calculations were done. All results are compared with experimental data, is widely known in the literature. This methods and the obtained analytical formulas synchronous oscillating movements of solids can be used to solve a wide range of vibrational modes management tasks.

Basic experimental laws are the following:

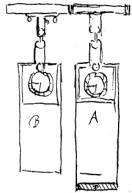
I.         Huygens. "Two of the pendulum clock hanging on the wall next to each other at a distance of one or two feet, to maintain consistency with the progress of such high precision that their pendulums always swayed together, without deviation" in the same direction.

II.      Huygens. "The clocks are placed in the enclosure, which, together with lead weights weighs just under 100 pounds. Swing of the pendulum are not, that they are moving parallel to each other, but rather, they approach and removed the opposite manner".

III.   Rayleigh. Watching two adjacent organ pipes, he found that at small detuning them they sound in unison. "If these frequencies differ little, the two tubes begin to sound the same frequency and sound in unison. Sometimes this is expressed in unison sound that sound completely disappears: each tube sounds, and at the same time there is no sound. "

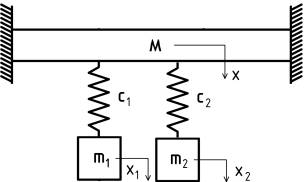
Consider two independent oscillator to a common rigid connection - fixed beam fig. 1. Such schematization does not contradict known scientific certainty because each autonomous oscillator can be interpreted in a self-oscillatory system with a constant flow of energy used during the period of the oscillations. Oscillations and the natural oscillations of a dynamical system have the same specific features - the frequency is set and is caused by the oscillator and its physical characteristics.

       

a                                                                          b

Figure 1 – The scheme of the oscillations of two autonomous oscillators fixed beam (a). Figure experimental Huygens’s studies (b).

 

Consider the linear dynamic model in Figure 1, and write its equation of motion to display and study of the influence of simple parameters of the mechanical system to the general oscillatory process

                                           , 

,                                                           (1)

                                           ,

where  , , , , , , 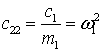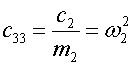; ,, − is the partial frequency beams, first and second oscillators, respectively;  − mass beams and cargo;  − the coefficients of the spring.

The system of motion equations (1) consists of the three connected homogeneous differential equations with non-separable variables, it is necessary to attach the initial conditions that are described in the experiments of Huygens and Rayleigh, for its full resolution.

,  ,                                     (2)

,  ,                                    (3)

Use the method developed in [3, 4] to separate variables and then solve the problem. The system (1) will be the equivalent of a new

,                    (4)

the coefficients of this system are given by the following formulas [3]

,  , .

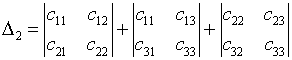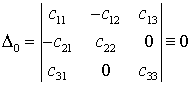The system (4) has a general characteristic polynomial of the sixth order

.                                             (5)

The motion laws of solids are determined on the basis of homogeneous differential equations solutions(4)

, (6)

, (7)

 (8).

where   ,  ,

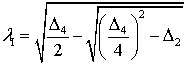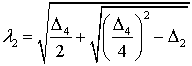,  ,                      (9).

It’s needed to complement the inequality for the existence of stable oscillatory modes [5]

.                     (10)

The algebraic equations system for the free coefficients Ài, Bi, Fi, i=  is obtained, solving common initial Cauchy problem. Moreover, the condition (3) determine the coefficients ,  ,  . The other conditions can accurately establish the relationships between other group settings

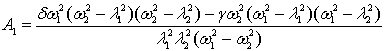, (11)

 

       

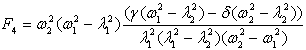
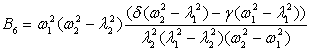
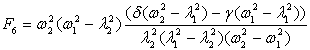
Solutions (6)-(8) take the form:

,                                    (12)

,                                  (13)

.                                 (14).

Each of the motion laws of rigid bodies M,  m1,  m2  (12)-(14) describes the natural oscillations of the general system of parallel-connected oscillators with frequencies l1 and l2 , inherent to a new force formed mechanical object. It’s necessary to implement the trigonometric conversion to determine which of the two oscillatory process in each of the formulas (12) - (14) is a priority

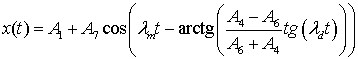,                     (15)

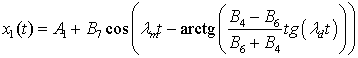,                     (16)

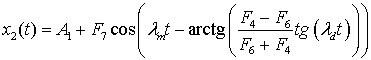,                           (17).

here , , ,  ,  . There are two new frequencies: the average , the frequency difference − 2, and the phase difference between the oscillations, which is a function of time and frequency and depends on frequency . These characteristics are due to the physical parameters of the oscillator − partial frequencies and , initial conditions − the kinematic excitation g, d  and the natural frequency of the mechanical system l1 ,  l2. the natural frequency of the mechanical system l1 << ld << lm << 2ld << l2 , then in general the vibrational mode of the mechanical system are observed from five to three frequencies. One of them determines the line profile of the vibrational modes envelope. Clearly they are presented in the figures in the group, consisting of the three frequencies. Thus of great importance is the amplitude of the corresponding harmonic function. Fluctuations with small amplitudes have little effect on the overall schedule as a whole.

Investigate vibrations of the form: y1=0.05cos(20.0t)-0.05cos(62.8t)=-0.0707sin(41.4t ± p/2)  fig. 2, where l1 = 20 rad/s (period T2), l2=62.8 rad/s (period T1)  have additional frequencies − lm=41.4 rad/s (period T3),  2ld = 42.8 rad/s (period T4),  ld = 21.4 rad/s (period T5). Five frequencies and five periods of oscillations respectively can be distinguished at the fig. 2,  T1 = 0.1 s,  T2 = 0.31 s,  T3 = 0.15 s, here  lm  2ld ,  T4 = 0.147 s,  T5 = 0.29 s  (ld  l1). Plot at the fig. 2 should be concerned with the periodicity oscillation phase  T4  , either (+ p/2) , or (− p/2):

,

,

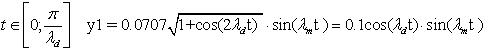The upper profile of the overall envelope oscillations having a frequency ld. is drawn by the dashed line on the plot at the fig. 2. In this example, all five natural frequencies of generalized mechanical system of two oscillators l1 << ld << lm << 2ld << l2  are displayed, reduced to the canonical form of the vibrational modes with their partial frequency of oscillation.

  

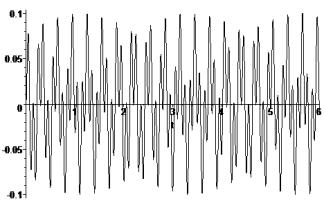
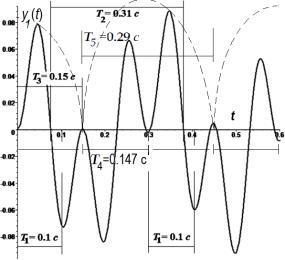
Figure 2 – Superposition of two vibrational modes

 

If the partial frequencies are close to their own or some additional frequencies then it’s operated only them in the literature. Nonlinear dynamics of the vibrational motions complicates studies of oscillating systems, identify common patterns and the possible impact on their respective physical, geometric, and other parameters. It’s difficult to determine the conditions for sustainable modes of functioning of the objects. Simple analytical formulas (10) - (17) make it easy to manage the properties synchronized events, in advance to identify and define its characteristics. Any non-linear math problem or model can be linearized by known methods, for example [6]. Further lets use the proposed formulas or methods to obtain explicit preliminary results.

Lets establish relationships between parameters that provide "in-phase" one-way synchronization, in which the phases deviation in (16) and (17) coincide

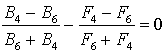,                                         (18)

and antiphase synchronization, in which the motion of the oscillator and oppositely directed in different directions with a phase difference of 180 degrees

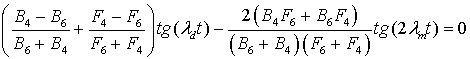.        (19)

The task of phase or antiphase synchronization is multiobjective, if it is required to add special conditions for the oscillation amplitudes and multivariate because they require physical characterization included in the partial frequencies, the initial perturbation of the system, the natural frequencies and the relation between all the frequencies present in it. This problem is easy to implement with modern calculations involving simple software environments. Formulas (18), (19) can be used for cases where the partial frequencies are not only close to each other, but multiples of each other for subharmonic oscillations.

The resulting mathematical relationships (10) - (19) can be used to solve management problems of vibrational modes in various fields of science. To confirm the experimental Huygens and Rayleigh laws, lets go to the limit passage in (11), (15) - (17), given the condition that the frequency w1 = w2 = l1 and, following the terms of classical literature, replace l1 = w1 ,  ,the following equations are obtained

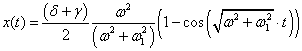,                                          s(20)

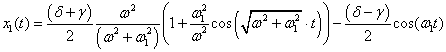,             (21)

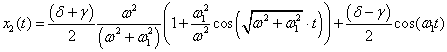.             (22)

The first terms in (20) and (21) are the same, the second terms are directly opposite in sign. This pattern was set Huygens in XVII century.

I. Considering the fact that the pendulum clock hung on the wall, in which the mass , then (20) - (22) we pass to the limit where

,       ,     .              (23)

This phenomenon of the clock synchronous consistent with high precision pendulum, together in the same direction, without deviation, even with different initial conditions, the Dutch scientist narrated in the postulate I.

II. Another experience was related to the fact that the clock is suspended in a heavy metal case and weighed together with goods less than 100 pounds (II). In this case, the mass Ì,  m1 , m2 are comparable in magnitude and order, neglect the frequency w is impossible, so the formulas (20) - (22), in which to put d = −g.

,     ,        .     (24)

III. Case, described by Rayleigh (III), in agreement with the same terms and conditions with respect to the physical parameters, as in the experience of Huygens, the only difference is that the initial conditions of excitation of the same organ pipes d = g  and (possible) partial frequency w = w1  are matched

, ,  (25)

Common musical instrument vibrations are the combination of two organ pipes x(t) + x1(t) and x(t) + x2(t), are absent. In this case, the vibrational modes of x(t) + x1(t)=g  and x(t) + x2(t) = g  mutually compensated. In this situation, each of the tubes has their sound, but that sound is not it special resonant frequency w1 or its surroundings (w1−e, w1+e) , but the frequency which is greater than it at times.

References

1. Blehman I.I. Sinhronization at the nature and technics/ I.I. Blehman – M.: Nauka, 1981. – 352 p.

2. Pikovskiy A.S. Sinhronization: Fundamental nonlinear phenomenon/A.S. Pikovskiy, M.G. Rozenblyum, U. Curte.-.M.:Tehnosphera, 2003.-494 p.

3. N.A. Dokukova and P.N. Konon General laws governing in mechanical vibratory systems// Journal of Engineering Physics and Thermophysics, 2006, Volume 79, Number 4, Pages 824-831, Publisher Springer New York, ISSN: 1062-0125.

4. N.A. Dokukova, E.N. Kaftaikina, S.V. Golod, M.V. Orehov, P.N. Konon //Experimental analysis of methods of calculating the dynamic of three-element mechanical system / Perspektywiczne opracowania sa nauka i technikami -2011:materialy VII miedzynarodowej naukowi-praktycznej konferencji, 7-15 listopada 2011r.– Przemysl: Nauka i studia, 2011.– .V. 51. – S. 19 – 25.

5. Voronov V.S. Sustainability performance of robust control systems // Math. RAS. Computer and Systems. 1995. ¹ 6. pp. 49-54

6. N.A. Dokukova, M.D. Martynenko and E.N. Kaftaikina Nonlinear vibrations of hydraulic shock absorbers// Journal of Engineering Physics and Thermophysics, 2008, Volume81, Number 6,Pages 1197-1200,Publisher Springer New York,ISSN:1062-0125.