*119802*

Аппроксимация колебаний при ударе

А.М.Данилов, И.А.Гарькина

Пензенский государственный университет архитектуры и строительства

Механические колебания при ударе обусловлены динамическими явлениями, связанными с наличием допусков, зазоров и поверхностных контактов отдельных деталей механизмов и сил, возникающих при вращении и возвратно-поступательном движении неуравновешенных элементов и деталей. Даже колебания с малой амплитудой часто вызывают резонансные колебания других элементов конструкций; усиливаются и становятся источником вибрации и шума.

Разработка методов защиты от удара и сопровождающих вибраций практически всегда связана с решением задачи экспоненциально-тригонометрической аппроксимации функции , заданной таблично (экспериментальные данные) на отрезке . Для определенности будем искать приближение выражением вида

,

где – чётный тригонометрический полином.

Для определения параметров и α экспоненциального множителя построим огибающую заданной функции, выделив из конечной последовательности модулей заданных значений функции строго убывающую, вогнутую последовательность ординат:

- построим (конечную) последовательность модулей заданных значений функций ,;

- извлечём из этой последовательности строго убывающую последовательность ,, сравнивая поочерёдно смежные члены; если данный член окажется не меньше предыдущего, то все предыдущие члены, которые не больше данного, исключаются;

- из полученной последовательности извлечем строго вогнутую последовательность , сравнивая поочерёдно угловые коэффициенты смежных звеньев полученной ломаной; если данный угловой коэффициент не больше предыдущего, то исключим все те предыдущие вершины ломаной, которые окажутся, ниже прямой, продолжающей влево данное звено. Ординаты вершин полученной ломаной и дадут требуемую конечную строго убывающую, строго вогнутую последовательность , где - отобранные значения независимой переменной , .

Далее полученную зависимость , аппроксимируем экспоненциальной функцией методом наименьших квадратов. Параметры A и α определятся из системы уравнений

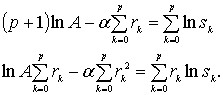
Затем по заданной таблице значений функции построим таблицу значений функции и интерполируем величину t чётным тригонометрическим полиномом

,

где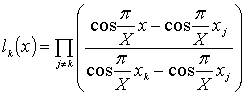

Окончательно:

.

В качестве иллюстрации рассмотрим экспоненциально тригонометрическую аппроксимацию экспериментальных данных (табличные значения , полученные по осциллограммам):

1	0,2967	19	0,2803	37	-0,0322	55	-0,1925	73	0,0430
3	0,0499	21	0,1622	39	-0,0156	57	-0,1668	75	0,0517
5	-0,3358	23	0,0932	41	0,0315	59	-0,1060	77	0,0549
7	-0,7092	25	0,0794	43	0,0772	61	-0,0380	79	0,0340
9	-0,5298	27	0,0769	45	0,0970	63	0,0366	81	-0,0100
11	-0,5676	29	0,0675	47	0,0717	65	0,0901	83	-0,0481
13	-0,1125	31	0,0409	49	0,0057	67	0,1051	85	-0,0451
15	0,2613	33	0,0057	51	-0,0897	69	0,0835	87	-0,0519
17	0,5613	35	-0,0284	53	-0,1655	71	0,0535	89	-0,0313

Определим параметры А и α экспоненциального множителя (график функции вписывается в область, ограниченную кривыми , ). Для этого по заданной последовательности значений функции, где (, n=44 – четное число) построим последовательность модулей этих значений и из неё извлечём строго убывающую последовательность , . А именно последовательность:

,,,,,; (q=5).

Угловые коэффициенты звеньев полученной ломаной (-0,0336; -0,0097;

-0,0073; -0,0050; -0,0033) строго возрастают; последовательность совпадает с выделяемой из неё строго убывающей, вогнутой последовательностью :,,;. Аппроксимируем эту последовательность функцией вида методом наименьших квадратов; A=1,13539, α=0,03618.

Далее функцию аппроксимируем частной суммой ряда Фурье, добавляя в неё новые члены до тех пор, пока не будет достигнута требуемая точность аппроксимации. В рассматриваемом случае функция на заданном отрезке обнаруживает приблизительную периодичность с периодом 2l=48=24h. Рассмотрим разложение на отрезке длиной 2l=48 тригонометрическим полиномом

(в данном случае достигается удовлетворительная точность; для достижения большей точности следует добавить новые члены).

Коэффициенты Фурье

,

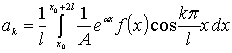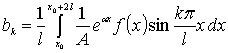
приближённо определялись по формуле Симпсона:

, ;

, ;

; ;

^.

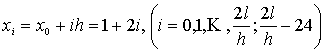Подставляя a₀= 0,07933, a₁= -0,17080, b₁= -0,13193, a₂= 0,23027,

b₂= -0,32187, a₃= 0,30377, b₃= 0,02186, получим

.

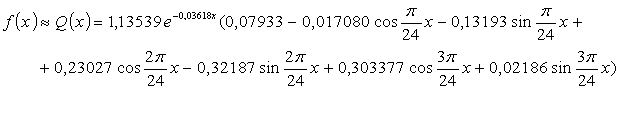Рассмотренный метод аппроксимации использовался при анализе работы упругого электропривода с учетом люфта и трения, в том числе в задачах управления объектами на подвижном основании; подтвердилась его эффективность.