*119924*
д.ф.-м.н., академик Божанов Е.Т., Исабаева Г.А.,
Аккасканова Н.Т.,
Жубанышбаева Р.Ж.
Казахский национальный
технический университет имени К.И. Сатпаева,
Алматы, Казахстан
Статика и динамика стержневых систем
в пределах и за пределами теории упругости
Рассмотрим метод уравнения
равновесия для случая больших смещении для стержневой системы, при котором
нужен непосредственного интегрирования общих нелинейных уравнений теории
упругости по z получают уравнения равновесия и граничные условия [1]. Тогда,
зная функции перемещения определяем форму критической деформации поперечного
сечения, а так же активную критическую нагрузку в виде 
для статических
сил и
для динамических
сил.
Здесь
− форма поперечного сечения, 
− модуль упругости, 
− модуль сдвига, 
− коэффициенты
взаимного влияния из допущении о существовании упругого потенциала для любого анизотропного материала
− характеристика толщины, 
− характеристика длины.
Теперь, записав динамику упругого
стержня:
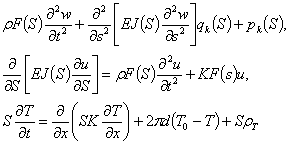(1)
Составим математическую модель Б-1
изгиба стержневой системы изогнутой оси волокна:
(2)
Здесь:
− продольное
перемещение, 
− поперечное
перемещение, 
− плотность, 
− площадь
поперечного сечения, 
− модуль
упругости, 
− момент
инерции, 
− элементы
матрицы жесткости, 
− площадь
поперечного сечения, 
− температура, 
− удельная
теплоемкость, 
− коэффициент
теплопроводности, коэффициент теплообмена с внешней средой, 
− наименьший
диаметр поперечного сечения, 
− температура
внешней среды, 
− плотность
источников, 
− коэффициент,
связанный со изгибом и изгибающим моментом поперечного сечения.
Если на стержневую систему действует реактивная сила, связанная
с кольцевым сжимающим усилием, приводящей к поперечной нагрузке, то Б-2
(3)
где
− коэффициент из матрицы жесткости.
Если на стержневую систему действует
ещё продольная критическая нагрузка, приводящая к изгибу, то Б-5:
(4)
где
− коэффициент
продольной критической нагрузки.
Таким образом, из математических моделей Б-1, Б-2 и Б-5 заключаем, что
учёт геометрической нелинейности приводит к изгибу стержневых систем за пределами теории упругости с линейным
упрочнением.
(5)
Здесь
− изгибающий момент упругой области, 
− изменение
момента, которое вызывается
отклонением материала от закона Гука.
В качестве примера рассмотрим
диаграмму растяжения − сжатия материала балки рис №1.
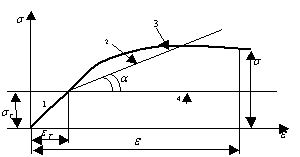
Рис. №1
В упругой зоне сечения справедлив закон Гука,
рис №1, прямая 1.
В линейно упрочненной зоне рис №1, прямая 2 получим материал с линейным
упрочнением с модулем пластичности.
, где 
− угол наклона прямой 2 к оси
.
Зависимость между напряжением и
деформацией в упрочнений − пластической зоне рис №1, кривая 3 можно
принять аппроксимацией степенной зависимости от свойства материала на участке
управления.
В идеально – пластической зоне рис №1 прямая 4 получим материал
диаграммы Прандтля [2].
Итак, для конкретного вида сечения
необходимо найти диаграмму деформирования моментов
и 
(6)
где
− радиус
кривизны нейтральной поверхностью, проходящей через ось ОХ сечения, 
− кривизны ее.
Следовательно, закон связи
интенсивности напряжения с интенсивностью деформации зависит от материала тела
и диаграммой работы материала на растяжение и кручение.
(7)
Тогда
геометрической нелинейной теории
изгиба стержневой системы изогнутой оси волокна в общем случае можно принять
математическую модель:
(8)
Здесь: 
− коэффициент,
связанный с изгибающими моментом в плоскости
ZX, 
− коэффициент,
связанный с касательной нагрузкой или с временем релаксации материала
(9)
где
− вязкость, E –
модуль Юнга, 
− коэффициент,
связанный с кольцевым сжимающим усилием, приводящий к поперечной нагрузке или
из трехэлементной модели упруго-вязкого материала: стандартного линейного тела
[3]; из двух пружин и одного демпфера;
из одной пружины и двух демпферов.
Литература
1.
Божанов Е.Т, Ибраимкулов. А.М. «Статистика деформируемых систем называется действием статистических нагрузок»,
современные проблемы дифференциальных уравнений, термин генераторов космических технологии, Алматы,
2006 г, стр. 186-187.
2.
Герасимов В.И., Герасимоа Е.В., “Метод координат трех моментов для определения
перемещения балок и рам”, Вестник АТИРПиХ, М, 1993, Вып.1, стр. 28-31.
3.
Ишлинский А.Ю. “ Продольные колебания стержня при наличии линейного закона
последствия и релаксации”, Прикладная математика и механика, 1940, Т.Ч. вып.1.,
стр. 79-92