Технические науки/2. Механика

Поддевалин В.М., Буторева В.С., к.т.н. Гурвич Ю.А.

ГУО «Институт пограничной службы Республики Беларусь»

Многокритериальная оптимизация параметров рулевой трапеции автобуса «МАЗ» при переменном значении шкворневой колеи и базы машин

В данной статье описывается алгоритм и комплекс программ, который позволяет: на стадии проектирования колесных машин создать шестизвенную рулевую трапецию для целого семейства автобусов и автомобилей с разными базами и колеями.

Под механико-математической моделью рулевой трапеции понимается совокупность схемы (рисунок 1) и формализованной связи − математического описания b = b(a,l₁,..,l_j,g₁,..,g_m), где b – угол поворота внешнего управляемого колеса машины; a - угол поворота внутреннего колеса; l₁,…,l_j – управляемые параметры; j – количество управляемых параметров; g₁,…,g_m – неуправляемые параметры; m- количество неуправляемых параметров.

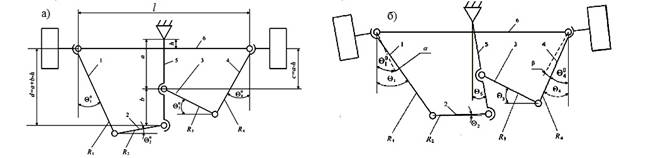Рисунок 1 − Схема рулевой трапеции автобуса «МАЗ»: а) колеса автобуса находятся в нейтральном положении; б) внутреннее колесо автобуса, совершающего левый поворот, повернуто на угол a, наружное колесо − на угол b

При синтезе параметров шестизвенной рулевой трапеции используется зависимость угла поворота наружного колеса от угла поворота внутреннего колеса α и других конструктивных параметров:

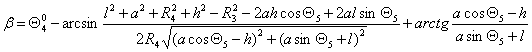, (1)

где , ,

В общем виде движение пневмоколесной машины без рулевой трапеции по криволинейной траектории без бокового скольжения колес описывается зависимостью:

b_N=b_N (a,l¢_1N,…,l¢_mN), (2)

где l¢₁,…,l¢_m - различные параметры машины (геометрические, инерционные и т. д.); m - количество параметров; b_N – угол поворота внешнего управляемого колеса машины.

В литературе (2) известно как уравнение котангенсов (или как уравнение идеального поворота машины):

ctgβ_N − ctgα = L /M, (3)

где L – шкворневая колея машины (в формуле (1) Ɩ=L); M– база машины.

Чтобы движение машины с рулевой трапецией наилучшим образом

(тем не менее, − приближенно) отобразило зависимость (3), необходимо варьировать все значения управляемых параметров l1,…,lj. Затем из набора совокупностей значений параметров выбирается такая совокупность параметров (l₁, l_j; g₁, g_m), которая соответствует максимальному приближению (или близости) (1) к (3). При этом возникают вопросы, что принять за меру близости двух зависимостей и как выразить математически степень близости зависимостей b и b_N друг к другу?

Из функционального анализа известно, что в пространстве функций x(t), определенных и непрерывных при a ≤ t ≤ b существуют различные нормы: чебышевская с равномерной сходимостью по ней и гильбертовская со среднеквадратичной сходимостью.

Примем за меры близости двух зависимостей: теоретической b_i и идеальной b_Ni – норму Гильберта F (где i – число точек на кривых), которую используем в качестве критерия оптимальности − показателя, оценивающего износ шин и качество проектирования технической системы:

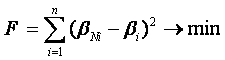^. (4)

Известны размеры и углы несимметричной шестизвенной рулевой трапеции (рисунок 1,а). При повороте стержня 1 на угол α стержень 4 повернется на угол β (рисунок 1,б).

Из восьми параметров в (1): Ɩ, R1, R2, R3, h, Θ1, Θ2, Θ3 − независимых шесть, так как имеет место четыре связи.

Постановка задачи синтеза. Варьируя шестью независимыми параметрами в различных сочетаниях, реализовать − гильбертовскую норму со среднеквадратичной сходимостью, при переменных значениях шкворневой колеи Ɩ и баз М машин.

Выбор оптимальных параметров рулевой трапеции по критерию износа шин (который формализован в виде нормы Гильберта) при постоянных величинах шкворневой колеи Ɩ и базы машины M осуществляется методами нелинейного программирования. При одновременном варьировании
k − значениями шкворневой колеи и q − значениями базы машин реализация (4) осуществляется методами многокритериальной оптимизации. Это резко усложняет решение задачи: количество вычислительных процедур возрастает в k_*q раз.

Параметры оптимизации:

R1 − продольный рычаг рулевой трапеции;

R2 – поперечный рычаг рулевой трапеции;

R3 – поперечный рычаг рулевой трапеции;

− угол наклона R1 к продольной оси машины;

− угол наклона R2 к поперечной оси машины;

− угол наклона R3 к поперечной оси машины;

Ɩ_k – колеи машин;

M_q – базы машин.

Параметрические ограничения:

R1min ≤ R1 ≤ R1max;

R2min ≤ R2 ≤ R2max;

R3min ≤ R3 ≤ R3max;

min ≤ ≤ max;

min ≤ ≤ max;

min ≤ ≤max;

Ɩmin ≤ Ɩ ≤ Ɩmax;

Mmin ≤ M ≤ Mmax.

Алгоритм многокритериальной оптимизации параметров шестизвенных рулевых трапеций различных конструкций реализован в виде программного пакета «Trapezia», который позволяет:

впервые решить задачу однокритериальной (критерий – износ шин) оптимизации параметров несимметричных шестизвенных рулевых трапеций при постоянных значениях базы M и колеи Ɩ машины;

создать оптимальную шестизвенную рулевую трапецию при переменных сочетаниях баз M_q и шкворневой колеи Ɩ_k машин;

сократить сроки проектирования машин и повысить их качество.

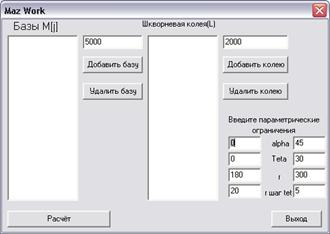
Рисунок 2 − Главное окно комплекса программ оптимизации параметров шестизвенных рулевых трапеций с переменной колеей и базой машин

В главном окне рисунка 2 находятся два списка «Список баз M,мм» и «Список колей L,мм (в нашем случае Ɩ)» куда заносятся значения размеров баз и колеи, посредствам кнопок «Добавить базу» и «Добавить колею».

В случае постоянных значений базы и шкворневой колеи машины в главное окно рисунка 2 заносится по одному значению Ɩ и M.

В случае переменных значений базы и шкворневой колеи машины в главное окно рисунка 2 заносится значения размеров баз и колеи из соответствующих полей Mmin ≤ M ≤ Mmax, Ɩmin ≤ Ɩ ≤ Ɩmax.

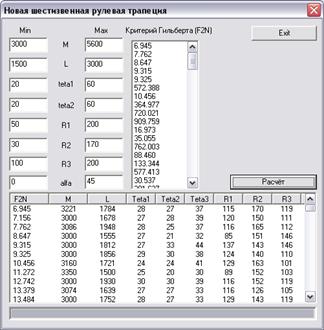
Рисунок 3 − Окно с результатами оптимизации несимметричной шестизвенной рулевой трапеции с переменной колеей и базой машин

В поля в столбцах «Min» и «Max» вводятся нижняя и верхняя границы интервалов значений параметров, которые задаются пользователем: R1min, R1max, R2min, R2max, R3min, R3max, min, max, min, max, min, max.

Резюме. Разработан комплекс программ многокритериальной оптимизации параметров шестизвенных рулевых трапеций различных конструкций (симметричных и несимметричных) при постоянных значениях базы M и колеи Ɩ машины и при переменных сочетаниях баз M_q и шкворневой колеи Ɩ_k машин.

Комплекс программ позволяет: на стадии проектирования колесных машин создать оптимальную рулевую трапецию для целого семейства автобусов и автомобилей (с разными базами и колеями); сравнивать существующие конструкции рулевых трапеций колесных транспортных средств с оптимальными и наметить пути их улучшения.