Economics/4. Investment activity and stock markets.

dr. of sci. Pistunov I.M.

HEI “National Mining University”, Ukraine

Model of investment portfolio optimization

Many researchers and practitioners traders investigate the problem of optimal portfolios formation. This method is an effective tool for filtering incoming data on securities volatility. As for research works relevant for CIS countries, a significant contribution to the theory of optimal investment portfolio.

Despite the existing variety of scientific and practical approaches to formation of investment strategy and risk management, classical Markowitz and Sharpe models are widely applied for direct distribution of funds among the assets.

The aim of this study is to improve the investment portfolio optimization model by combining existing Markowitz and Sharpe models.

Pistunov-Sitnikov risk-revenue model. The model was created as a solution to multicriteria optimization task ensuring risk minimum and profit maximum. As a result convolution of two Markowitz criterion was formed. Whereby the criterion of "minimum" was placed in the numerator and the criterion of "maximum" - the denominator. Also, the numerator was added to the weighted average variance portfolio. The main idea of this model was to unite the Markowitz model with maximum rate of return and minimum risk.

Its advantage over the previously described models is that there is no need to determine the acceptable level of risk and income. This model requires the same statistical calculations as Markowitz model. This model works great with small number of assets and with relatively volatile stock market (1).

Integrated Pistunov-Sitnikov-Sharpe model.

We use the Pistunov-Sitnikov approach, that allows assembling two Markowitz models into one by putting the rate of return into numerator and the risk into the denominator.

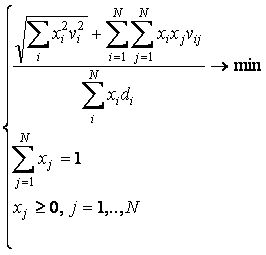(1)

where d_i – average rate of return of asset i, v_i– variation (standard deviation) rate of return on asset i, v_ij – covariance of profitability of assets j and i, x_i,j – the share of capital spent on the purchase of securities i and j.

Considering the Sharpe model we have R_f – rate of return on the risk-free asset. Elimination of this parameter provides us with portfolio level of profitability i.e. maximum aiming function.

But there is a rate of return index in the denominator of Pistunov’s optimal portfolio model.

This inequality ensures the implementation of the premise that the risk of the portfolio should not exceed pre-specified risk frontier. The counterpart of this constrain is also present in the Markowitz model, as well as set beforehand expected portfolio return. But the model Pistunov-Sitnikov allows to omit the definition of such values as predefined profit and risk. On the top of that, the index that characterizes risk (β_i) is present in the denominator. Therefore, the Sharp’s model constrain is discarded completely. So a simplified version of the denominator is multiplied by the denominator of Pisunov’s model and the numerator remains unchanged.

Thus, Integrated Pistunov-Sitnikov-Sharpe model is (2).

The model was tested on real data of equities of the energy sector, traded on the New York Stock Exchange with next results (table 1). Especially for this comparison criterion of relative riskiness was developed, that is calculated according the formula:

Vr = R/M,

where R – risk, а M – rate of return of asset.

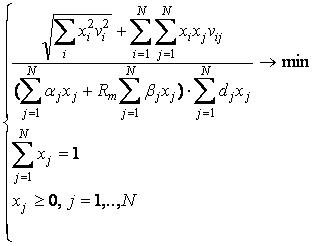(2)

Table 1 - Comparison of calculations on optimization models

Model	A	AE	DTEE	EI	En	PSEG	Vr
Developed integrated model	23%	34%	23%	6,6%	1,7%	13%	0,0007
Pistunov-Sitnikov model	23%	43%	25%	3,1%	0,0%	6,9%	0,0008
Sharpe model	0,0%	0,0%	23%	52%	25%	0,0%	0,0472
Markowitz (risk minimization)	92%	8,5%	0,0%	0,0%	0,0%	0,0%	0,1028
Markowitz (profit maximization)	21%	79%	0,0%	0,0%	0,0%	0,0%	0,1036

Legend for corporations: A – Ameren, AE – American electric, DTEE – DTE Energy, EI – Edison international, En – Enbridge, PSEG – Public Service Enterprice Group,

The obtained results indicate that the developed integrated model is the most effective among models considered on the rate return criteria. This conclusion is supported with the criterion of relative riskiness that was developed specially for this study. The relative riskiness (0.000702) is minimal for the portfolio formed on integrated model.