К.т.н. Шепетюк Б.Д., д.ф.-м.н. Нестерук І.Г.

Чернівецький національний університет імені Юрія Федьковича, Чернівці, Інститут гідромеханіки НАН України, Київ, Україна

Форми тонких осесиметричних стаціонарних штучних каверн при наявності вертикального потоку води

Опір високошвидкісних підводних транспортних засобів, може бути зменшений шляхом зменшення площі, яка змочується водою, тобто за допомогою використання суперкавітаціі ([1-3]). Для отримання малих значень числа кавітації при малих швидкостях або на великих глибинах руху, використовується піддув каверни газом ([4]). Вентиляція також дуже важлива в експериментах, оскільки швидкості в експериментальних установках, як правило, набагато менші, ніж для реальних транспортних засобів. Обмежені швидкості кавітаційних труб суттєво збільшують вплив гравітації на форми і розміри каверни.

Теоретичні та чисельні дослідження вентильованих каверн вельми обмежені. Навіть в тому випадку, коли вплив потоку газу усередині каверни і гравітації незначні, немає повної теорії для форми каверни в залежності від швидкості подачі газу, числа кавітації і форми тіла, розташованого усередині каверни. Якщо газ рухається у вузькому каналі між поверхнею каверни і корпусом транспортного засобу, то тиск на поверхні каверни не є постійним і змінює її форму в порівняні з випадком парової кавітації. Це складне явище досліджувалось чисельно з використанням рівнянь в'язкої рідини [5]. Використання моделі ідеальної рідини і теорії тонкого тіла дозволяє отримати прості рівняння для форми осесиметричних вентильованих суперкаверн, якщо потік газу між поверхнею каверни і тіла обертання є одновимірним, нев'язким і нестисливим. Деякі цікаві результати були отримані в роботах [6-8] для стаціонарного потоку рідини без гравітаційних ефектів.

В роботі [9] результати цих робіт узагальнені для нестаціонарних вертикальних потоків в полі сили тяжіння. Зокрема, було запропоновано рівняння першого наближення для радіуса R(х) стаціонарної осесиметричної вентильованої каверни:

(1)

де всі довжини є безрозмірними (віднесені до радіусу каверни в її початку R₀); k = 1 відповідає випадку, коли напрямки потоку води на нескінченності і гравітаційного прискорення збігаються; k = -1 відповідає випадку, коли напрямки цих векторів протилежні. Значення параметрів s₀, Fr, D і a визначаються формулами:

, F_r = ,

α =

де r - густина води; U - стала швидкість потоку води на нескінченності; p_v-тиск водяної пари при температурі навколишнього середовища; p_¥ і p₀ тиски, виміряні в поперечному перерізі каверни далеко в потоці води і газі на початку каверн відповідно; p_g постійна густина газу; Q – об’ємне витрачання газу; R_b, R_b0 радіуси корпусу в точках х і х = 0; e малий параметр, відношення максимального радіуса системи каверна-кавітатор до його довжини.

У цьому дослідженні ми зосередимося на числових рішеннях рівняння (1) при різних значеннях числа Фруда Fr і параметра k = -1. Розрахуємо форми і розміри вентильованих каверн і проаналізуємо критичні значення інтенсивності піддуву.

Для інтегрування дифрівняння (1) використовувалися стандартні початкові умови в точці сходу каверни х = 0 і метод Рунге-Кутти 4-го порядку .

R = 1, dR/dx = b

Розрахунки показали, що для співпадаючих напрямків сили тяжіння та потоку рідини на нескінченності (k = 1) розміри каверни обмежені при будь-якій інтенсивності піддуву газу. Схожа ситуація в випадку природної кавітації, коли розв’язок рівняння (1) має такий вигляд (див. [10]):

(2)

Оскільки lne <0, то многочлен (2) може досягти нульових значень при досить великих значеннях х при будь-яких числах Фруда. Таким чином, довжина кавітатора і діаметр тіла завжди обмежені.

Інша ситуація виникає при протилежних напрямках сили тяжіння і швидкості потоку навколишнього середовища (k = -1). При деякому критичному значенні числа Фруда графік полінома (2) дотикається осі х. Збільшення числа Фруда дає необмежені каверни, котрі не можуть бути реалізовані відповідно до принципу стійкості [11]. Відповідні критичні числа Фруда були обчислені в роботі [10] для парових каверн і R_b₀ = 0. Результати розрахунків форм вентильованих каверн представлені на рис. 1-3 при k = - 1 для різних кавітаторів (b = 0,1; 0; - 0,1) та різних значеннях інтенсивностей піддуву.

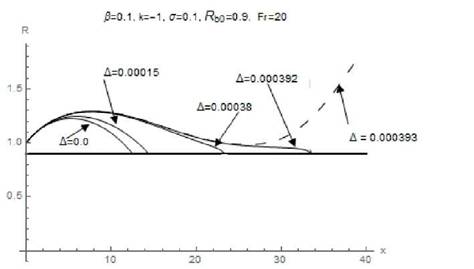
$Описание: C:\DOCUME~1\9335~1\LOCALS~1\Temp\FineReader10\media\image1.jpeg$

Рис. 1. Форми вентильованих каверн, створених тонким конічним кавітатором b =0,1 при k = - 1, Fr = 20, R_b₀ = 0,9; s₀ = 0,1.

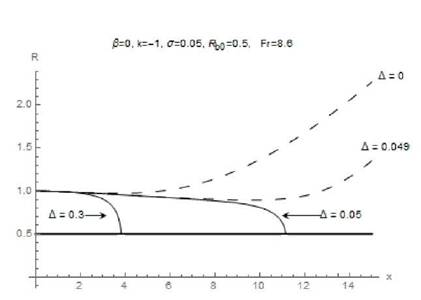
$Описание: C:\DOCUME~1\9335~1\LOCALS~1\Temp\FineReader10\media\image5.jpeg$

Рис. 2. Форми донних вентильованих каверн, b = 0 при k = -1, F_r = 8.6, R_b₀= 0,5; s₀ = 0,05.

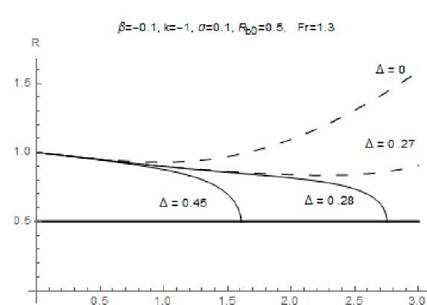
$Описание: C:\DOCUME~1\9335~1\LOCALS~1\Temp\FineReader10\media\image6.jpeg$

Рис. 3. Форми донних вентильованих каверн, b = - 0,1 при k = - 1, F_r = 1.3, R_b₀ = 0,5, s₀ = 0.1.

Для тонкого конічного кавітатора b ³ 0, розміри вентильованих каверн збільшується зі збільшенням інтенсивності вентиляції (рис.1). При проходженні критичного значення параметра вентиляції (D » 0,0003925) каверна дотикається циліндричного корпусу і стає нескінченною. Оскільки невелика зміна параметрів повинна викликати невеликі зміни в потоці (відповідно до принципу стійкості, дивись, наприклад, [11]), швидкість потоку не може перевищувати цього критичного значення. Нереалістична нескінченна каверна показана пунктирною лінією. Подібні обмежені значення інтенсивностіі вентиляції властиві також циліндричним тілам в рідині без гравітації ( див. [6]).

Довжина донних каверн (b £ 0) зменшується зі збільшенням інтенсивності піддуву (рис. 2 та 3). При проходженні критичного значення параметра вентиляції каверна дотикається циліндричного корпусу і стає нескінченною. Оскільки невелика зміна параметрів повинна викликати невеликі зміни в потоці (відповідно до принципу стійкості, дивись, наприклад, [11]), то інтенсивність піддуву потоку не може бути менше цього критичного значення. Нереальні нескінченні каверни показані на рис. 2 і 3 пунктирними лініями. Подібні обмежені значення інтенсивності піддуву властиві також циліндричним корпусам в невагомій рідини ( див. [7]).

Таким чином, з використанням відомого диференціального рівняння першого наближення, були розраховані форми тонких стійких осесиметричних вентильованих каверн в потоці води, спрямованому вгору при різних значеннях числа Фруда і радіуса циліндричних корпусів, що знаходяться всередині каверни. Було показано, що вентиляція збільшує розміри каверн, створених конічним кавітатором, і зменшує довжину донних каверн. Коли напрямок потоку води на нескінченності протилежний напрямку сили тяжіння, інтенсивність піддуву не може перевищувати деяке критичне значення для конічного кавітатора і не може бути менше деякого критичного значення для донних каверн.

Література:

1. Logvinovich G.V. Hydrodynamics of Flows with Free Boundaries.-Halsted, 1973. - 208 p.

2. Savchenko Yu. N. Perspectives of the Supercavitation Flow Applications// Int. Conf. on Superfast Marine Vehicles Moving Above, Under and in Water Surface (SuperFAST'2008), 2-4 July 2008. St. Petersburg, Russia.- 2008.

3. Nesteruk "Drag drop on high-speed supercavi- tating vehicles and supersonic submarines", Applied Hydromechnics, vol. 17, N 4, pp. 52 - 57, 2015. http://hydromech.org.ua/content/pdf/ph/ph-17-4

4. Vlasenko, Yu. D, Savchenko, G. Yu. 2012 Study of the parameters of a ventilated supercavity closed on a cylindrical body, I. Nesteruk (ed.). Supercavitation, Springer, pp. 201-214.

5. Zhuravlev, Yu. F., Varyukhin, A.V. 2008 Numerical simulationof interaction gas jets flowing into water cavity with its free surfaces simulation, Int. Conf. SuperFAST2008, Saint-Petersburg, Russia.

6. Манова З.І., Нестерук І.Г., Шепетюк Б.Д. Оцінки впливу вентиляції на форму тонких осесиметричних каверн // Прикладна гідромеханіка. – 2011. –Т13(85), N 2. – С44-50.

7. Нестерук І.Г., Шепетюк Б.Д. Особливості форми донних штучних осесиметричних каверн // Прикладна гідромеханіка. – 2011. –Т13(85), N 3. – С64-75.

8. Нестерук І.Г., Шепетюк Б.Д. Форма штучних осесиметричних каверн при до – та надкритичних значеннях інтенсивності піддуву// Прикладна гідромеханіка. – 2012. –Т14, N 2. – С53-60.

9. Nesteruk, I. Shape of Slender Axisymmetric Ventilated Supercavities, Journal of Computational Engineering, vol. 2014, Article ID 501590, 18 pages, 2014. doi:10.1155/2014/501590.

10. Nesteruk I. On the Shape of a Slender Axisymmetric Cavity in a Ponderable Liquid// Fluid Dynamics. DOI: 10.1007/BF01052000. -1979.- V.14(6). - P. 923 - 927.

11. Nesteruk I. The restrictions of the parameters of cavitational flow// Pmm Journal of Applied Mathematics and Mechanics - 1986. - V. 50, No. 4. - P. 446-449, DOI: 10.1016/0021-8928(86)90007-9.