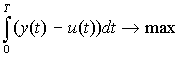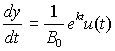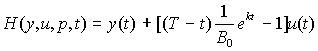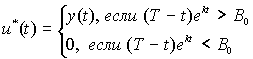Экономические науки/8. Математические методы в экономике

К.э.н. Диленко В.А.

Одесский национальный политехнический университет

Учет НТП в задаче оптимизации динамики

национального дохода

Одним из актуальных направлений современных экономико-математических исследований является постановка и решение задач рационального хозяйствования с учетом влияния инновационных факторов. На макроэкономическом уровне к таким исследованиям может быть отнесена задача оптимизации динамики национального дохода. В научной литературе, насколько нам известно, указанная задача, с непосредственным отражением в ней воздействия НТП на особенности роста национального дохода, в приведенной ниже постановке еще не рассматривалась.

Для математической формулировки данной задачи будем использовать известное [1, 280] дифференциальное уравнение динамики национального дохода (НД)

,

(1)

где - величина НД в момент времени , - величина производственного накопления, - капиталоемкость национального дохода, - величина непроизводственного потребления.

Введем в данную модель инновационный фактор. Будем полагать, что под воздействием научно-технического прогресса величина капиталоемкости

с течением времени снижается согласно закону

,

(2)

где - капиталоемкость НД в начальный момент времени, т.е. , k – параметр, определяющий темп снижения указанной капиталоемкости.

По аналогии с [1, 289] на основе математической модели (1), (2) можно сформулировать задачу определения траекторий динамики НД и его составляющих , , доставляющих максимум показателю величины суммарного непроизводственного потребления на интервале времени

,	(3)
,	(4)
.	(5)

Заметим, что в соотношении (4) величина имеет форму и отвечает экономическому содержанию мультипликатора прогресса [2, 91], для которого является начальной эффективностью производственного капитала. Таким образом, (4) в модели отражает воздействие автономного НТП, материализованного в производственных фондах, и соответственно параметр k должен интерпретироваться как темп прироста величины национального дохода за счет воздействия НТП.

Оптимизационная модель (3) – (5) представляет собой задачу оптимального управления, в которой управляющим параметром является величина производственного накопления , а фазовой координатой объем НД .

Функция Гамильтона для данной задачи имеет вид

.

(6)

При максимизации по с учетом ограничения (5) получаем выражения для оптимальной траектории

.

(7)

Анализ (7) показал, что в зависимости от соотношения значений параметров и возможны несколько видов оптимального решения задачи (3) – (5), однако в качестве принципиально различных можно выделить следующие.

Если для указанных параметров выполняются неравенства

, ,

(8)

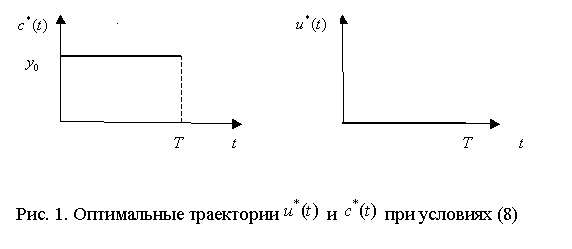то оптимальные траектории производственного накопления и непроизводственного потребления имеют вид, представленный на графиках рис. 1 ( величина НД в начальный момент времени).

Таким образом, при выполнении неравенств (8) оптимальное решение задачи (3) – (5) состоит в том, что величина национального дохода на протяжении всего анализируемого периода равна первоначальной и он в полном объеме должен направляться на непроизводственное потребление, производственное накопление полностью отсутствует.

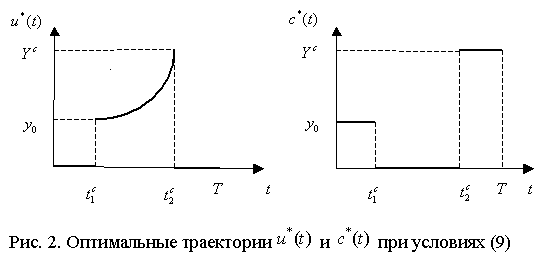
Для случая, определяемого соотношениями

, ,

(9)

оптимальное решение рассматриваемой задачи отображается графиками рис. 2, где и соответствующие точки переключения, .

Согласно полученному оптимальному решению весь НД, имеющийся на начальный момент времени и сформировавшийся к некоторому моменту , направляется соответственно при и на непроизводственное потребление, производственное накопление осуществляется на интервале времени .

При значениях параметров , для которых справедливы неравенства

, , ,

(10)

решением задачи (3) – (5) являются оптимальные траектории и , представленные на графиках рис. 3.

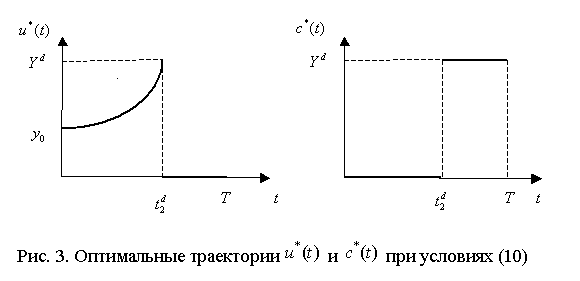
В соответствии с полученным решением в данной ситуации весь плановый период разбивается на два временных интервала. При весь НД направляется на производственное накопление, благодаря чему происходит его рост, непроизводственное потребление полностью отсутствует. На втором интервале национальный доход используется только на непроизводственное потребление, соответственно его величина сохраняется на неизменном уровне .

Полученная система решений задачи оптимального управления динамикой национального дохода (3) – (5), их анализ позволяет сформулировать некоторые общие вывода о влиянии учитываемых в модели экзогенных факторов (и в первую очередь НТП) на особенности оптимального развития рассматриваемой экономической системы:

- повышение интенсивности НТП стимулирует стратегию достижения максимального суммарного непроизводственного потребления за счет активизации процессов использования НД на производственное накопление;

- увеличение продолжительности планового периода , также приводит к росту (в абсолютном и относительном измерении) интервала времени, для которого оптимальным является использование всего национального дохода на производственное накопление;

- увеличение исходной капиталоемкости НД является сдерживающим фактором производственного накопления, его рост инициирует развитие “стратегии проедания”, вплоть до использования на цели непроизводственного потребления всей массы продуцируемого национального дохода в течение всего рассматриваемого периода времени.

Литература:

1. Гранберг А. Г. Моделирование социалистической экономики. - М.: Наука, 1988. - 487 с.

2. Плакунов М. К., Раяцкас РЛ. Производственные функции в экономическом анализе. — Вильнюс: Минтис, 1984. — 308 с.