Економічні науки/8. Математичні методи в економіці

К.е.н., доцент Потапова Н. А., Антох О. М.

Вінницький національний аграрний університет, Україна

Павутиноподібна модель ціноутворення

За останні роки швидкими темпами розвиваються дослідження в сфері ціноутворення за допомогою павутиноподібної моделі. Стійкість та стабільність ринкової рівноваги має важливе значення в економіці. Ринок може саморегулюватися, тобто досягати рівноваги за допомогою своїх внутрішніх сил, і тому додаткове його регулювання не є необхідним. Але якщо рівновага ринку порушується, то необхідно відшукувати засоби для її регулювання. Таким засобом регулювання та відновлення стабільності ринку виступає павутиноподібна модель ціноутворення.

Павутиноподібна модель ціноутворення – це одна із класичних економіко-математичних моделей, що дозволяє досліджувати стійкість цін та обсягів товарів на ринку, який описується традиційними кривими попиту та пропозиції при наявності запізнення в часі (лага) одного з процесів. Етапи встановлення рівноважної ціни на ній набувають форму спіралі, яка разом з лініями попиту і пропозиції нагадує павутину. Павутиноподібна модель покликана показати як саме виробник встановлює рівноважну ціну [1, с. 136].

Відомо, що найбільший обсяг продажів досягається саме завдяки рівноважній ціні. Але як її визначити? Криву пропозиції побудувати досить легко, оскільки виробник знає можливості свого підприємства і склад витрат на виробництво, що дає змогу підрахувати скільки одиниць товару можна виготовити і продати за певною ціною. Проте криву сукупного попиту вкрай важко побудувати, а іноді й неможливо, особливо в разі випуску нового товару. Поки товар не надійде на ринок, не можна з упевненістю сказати якою буде величина попиту за тієї чи іншої ціни. Тому виробники при встановленні ціни спираються на власні прогнози, а потім коригують величину цін в залежності від реального попиту. Таким чином ціна товару коливається, в результаті чого вона може наблизитися до рівноважної, найбільш вигідної продавцям і покупцям [2].

Рівень підвищення чи зниження ціни виробником демонструють дві прості моделі:

- павутиноподібна модель із запізненням попиту;

- павутиноподібна модель із запізненням пропозиції.

В основі павутиноподібної моделі із запізненням попиту лежать наступні гіпотези:

- ринкова ціна встановлюється, виходячи з обсягу пропозиції щодо функції попиту (всі товари на ринку повинні бути продані);

- продавець визначає обсяг виробництва, виходячи з ринкової ціни минулого періоду.

В основі павутиноподібної моделі із запізненням пропозиції лежать такі гіпотези:

- ціна на ринку встановлюється продавцем, виходячи з обсягу пропозиції відповідно до кривої пропозиції;

- продавець визначає обсяг виробництва, виходячи з попиту минулого періоду;

- споживання не перевищує ні попиту, ні пропозиції [3].

Слід відзначити, що павутиноподібна модель може мати три стани ринку в залежності від специфічних характеристик ліній попиту і пропозиції (Рис. 1):

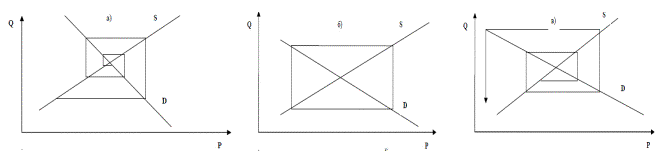
Рис. 1. Можливі варіанти зміни цін і об’ємів виробництва (а) стабілізація, б) циклічні зміни, в) нестабільність

1. Ринок знаходиться в стані стійкої рівноваги. Будь-які зміни, що відбуваються на ринку, не можуть змінити її. Відповідні зміни в об’ємах виробництва в кінцевому результаті зменшуються і призводять попит і пропозицію до стану ринкової стабільності.

2. Ринок перебуває в стані циклічних коливань. Це окремий випадок павутиноподібної моделі, що зустрічається дуже рідко. Проте теоретично він можливий і полягає в тому, що об’єми виробництва і попит, що склався, перебувають у постійних коливаннях.

3. Ринок – в нестабільному стані. Будь-які намагання зміни та коректування об’ємів виробництва призводять до додаткових і сильніших змін, і тому система в цілому має нестійкий, «вибуховий» характер [4, с. 144].

В основу павутиноподібної моделі закладена наступна математична залежність: (1)

де Q_t – об’єм попиту (пропозиції) в момент часу t;

α – постійна величина в лінійній залежності попиту;

β – постійна величина в лінійній залежності пропозиції;

a, b – коефіцієнти, які визначають кут нахилу ліній попиту і пропозиції (при цьому величина a від’ємна і характеризує спадну лінію попиту, а величина b звичайно позитивна і характеризує висхідну лінію пропозиції);

Р_t – ціна в момент часу t, по якій споживач готовий купити заданий об’єм виготовленої продукції;

Р_t-1 – ціна в момент часу (t-1), по якій виробник готовий реалізувати виготовлену продукцію споживачам [4, с. 145].

Проведення математичних перетворень дозволяє отримати прогноз ціни в будь-який момент часу. Вони мають наступний вигляд:

(2)

(3)

(4)

(5)

де Q_ср, P_ср – відповідно значення об’ємів виробництва і ціни продукції в точці ринкової рівноваги.

Зміст даної залежності полягає в тому, що виробник приймає рішення про виробництво продукції в наступному виробничому циклі на основі ринкової ситуації, що склалась на даний момент часу. При цьому рівень споживчих цін не дає повної інформації про можливий об’єм споживання і тому основу для визначення можливих об’ємів виробництва складає споживчий рівень цін [5].

Дослідники моделі вивели основні умови, котрі визначають характеристики моделі. До цієї умови відноситься значення показника b/a: якщо значення даного показника по модулю дорівнює 1, то модель буде циклічною, якщо більше 1, то модель рахується нестійкою, якщо ж значення показника менше 1, то модель буде тяжіти до точки ринкової рівноваги. На практиці найбільшу цінність будуть мати рекомендації про те, як необхідно приймати рішення в системі управління, щоб забезпечити системі стійкий стан. Алгоритм рішення даного питання:

1. Для того, щоб збільшити стійкість системи, потрібно коригувати можливе значення очікуваної ціни на який-небудь поправочний коефіцієнт К.

2. В цьому випадку динамічна павутиноподібна модель матиме вигляд:

(6)

(7)

(8)

(9)

(10)

2. На основі вивчення залежностей об’ємів попиту і пропозиції від ціни визначаються значення a і b. При цьому не важливо, як буде змінюватись положення самих графіків (значення α і β).

3. Визначивши значення показників a і b можна встановити необхідне значення поправочного коефіцієнта k таким чином, щоб вираз bk/a був більшим одиниці. Особливо це важливо в тому випадку, коли система потенційно нестійка і вираз b/a по модулю менший одиниці (чи дорівнює одиниці). Вирішуючи нерівність можна отримати умову, в якій значення поправочного коефіцієнта k повинне по модулю перевищувати відношення a/b на яку-небудь величину n, значення якої не повинне бути більше одиниці. Таким чином, знаючи характеристики попиту і пропозиції в системі управління можна встановити правила коригування прийняття рішення у відношенні майбутнього попиту на товари і послуги, які дозволяють позбутися від нестійкої системи [6, c. 28].

Сьогодні вивчення павутиноподібної моделі пішло далеко вперед від її класичного уявлення. Ця модель дозволяє дізнатися досить серйозно про внутрішній механізм ціноутворення, визначити основні параметри, що впливають на систему, і проаналізувати її поведінку. Зараз це не просто економічна модель — це складний математичний аналіз, що дозволяє пояснити, надалі не до кінця зрозумілий, процес зміни ціни і вивести схему коректного управління цінами на ринку.

Література.

1. Новожилова М. В. Моделювання економічної думки / . В. Новожилова, І. А. Чуб. – Харків, 2005. – 170 с.

2. Паутинообразная модель ценообразования. Модель с запаздыванием спроса [Электрон. ресурс]. – Режим доступа: http://www.school-collection.iv-edu.ru/dlrstore/ffed77b7-fea1-f8e3-5cc1-07ce87390a41/00139084797510261.htm

3. Лебедев, В.В. Математическое моделирование социально-экономических процессов / В. В. Лебедев. – М.: Изограф, 1997.

4. Шевченко, В. В. Использование паутинообразной модели при принятии перспективних решений // Наукові праці ДонНТУ. Серія: Економічна. – Вип. 87. – Д., 2004.

5. «Паутинообразная» модель ценообразования [Электрон. ресурс] // Тарасевич Л. Микроэкономика:[учебник] / Л. Тарасевич, П. Гребенников. – Режим доступа: http://economicus.ru/site/grebenikov/E_Micro/chap4/4_2/4_2.html

6. Давнис, В. В. Элементы экономико-математического моделирования. Лабораторный практикум / В. В. Давнис. – Воронеж, 2001. – 49 с.