Шнайдер І. М.
Науковий
керівник – Довгунь А.Я.
Буковинська
державна фінансова академія
Знаходження повного граничного доходу від функціонування економічної
системи за допомогою ланцюгів Маркова.
Розглянемо економічну систему, яка може
знаходитися в одному з несумісних
станів ξ = і кінцевого простору можливих станів ![]() . В процесі свого функціонування система в дискретні моменти часу, які будемо називати кроками і
позначатимемо як
. В процесі свого функціонування система в дискретні моменти часу, які будемо називати кроками і
позначатимемо як ![]() , переходить з одного стану
, переходить з одного стану ![]() в стан
в стан ![]() .
.
Зміна станів
проходить за наступним законом: в початковий момент часу (![]() ) ймовірність набуття системою початкових станів дорівнює
) ймовірність набуття системою початкових станів дорівнює ![]() , а потім на будь-якому кроці n умовна ймовірність
переходу системи зі стану
, а потім на будь-якому кроці n умовна ймовірність
переходу системи зі стану ![]() , в стан
, в стан ![]() дорівнює
дорівнює ![]() . Відмітимо, що ця ймовірність не залежить ні від станів
системи в попередні моменти часу (властивість марковості), ні від поточного
часу (властивість однорідності). [1]
. Відмітимо, що ця ймовірність не залежить ні від станів
системи в попередні моменти часу (властивість марковості), ні від поточного
часу (властивість однорідності). [1]
Означення 1. Випадковий процес ![]() зміни станів системи
зміни станів системи ![]() називаються простим
однорідним ланцюгом Маркова з кінцевим числом станів та дискретним часом, якщо
для всіх
називаються простим
однорідним ланцюгом Маркова з кінцевим числом станів та дискретним часом, якщо
для всіх ![]() і
і ![]() виконується
марківська властивість
виконується
марківська властивість
![]() (1)
(1)
при умові
![]() .
.
Ймовірності ![]() та ймовірності
та ймовірності ![]() ,
, ![]() , утворюють так званий стохастичний вектор, який задовольняє
наступні умови:
, утворюють так званий стохастичний вектор, який задовольняє
наступні умови:
![]()
![]() ,
, ![]()
![]() (2)
(2)
Означення 2. Матриця ![]() розмірності
розмірності ![]() називається матрицею ймовірностей переходу марківського
випадкового процесу
називається матрицею ймовірностей переходу марківського
випадкового процесу ![]() .
.
З рівності
(1) маємо:
а) для будь-якого n та всіх ![]() виконується рівність
виконується рівність
![]() , (3)
, (3)
тобто розподіл ймовірностей
станів дорівнює добутку ймовірностей початкового стану на відповідні
ймовірності переходу.
б) для всіх ![]() і всіх
і всіх ![]() виконується рівність
виконується рівність
![]()
![]() , (4)
, (4)
яка буде трактуватися наступним
чином: ![]() - стан системи в
теперішній момент часу,
- стан системи в
теперішній момент часу, ![]() – стан системи в
минулому,
– стан системи в
минулому, ![]() – стан системи в
майбутньому і при фіксованому теперішньому стані системи, минулі і майбутні
стани є незалежними. [1]
– стан системи в
майбутньому і при фіксованому теперішньому стані системи, минулі і майбутні
стани є незалежними. [1]
Розглянемо
економічну систему (фірму, підприємство, виробництво тощо) з кінцевим числом
станів ![]() , функціонування якої моделюється ланцюгом Маркова з матрицею
ймовірностей переходу
, функціонування якої моделюється ланцюгом Маркова з матрицею
ймовірностей переходу ![]() . При переході зі стану i в стан j система отримує
однокроковий дохід (можливо й від'ємний)
. При переході зі стану i в стан j система отримує
однокроковий дохід (можливо й від'ємний) ![]() , що не залежить від номеру кроку. Сукупність всіх однокрокових
доходів утворює квадратну матрицю
, що не залежить від номеру кроку. Сукупність всіх однокрокових
доходів утворює квадратну матрицю ![]() однокрокових доходів.
однокрокових доходів.
Дохід, який
може отримати некерована система за N кроків є випадковою величиною з розподілом ймовірностей,
що визначаються ймовірнісними зв’язками ланцюга Маркова. [2]
Означення 3. Математичне сподівання цієї
випадкової величини називається повним
очікуваним доходом за n кроків. [3]
Нехай в
деякий момент часу система знаходиться
в стані і та вона повинна
функціонувати n кроків. Позначимо ![]() повне очікування
доходу системи за n кроків. Цей дохід може
бути обчислений наступним способом. На першому кроці система переходить в стан j з ймовірністю
повне очікування
доходу системи за n кроків. Цей дохід може
бути обчислений наступним способом. На першому кроці система переходить в стан j з ймовірністю ![]() і при цьому отримує дохід
і при цьому отримує дохід ![]() . З цього стану система здійснює решта n – 1 крок і отримує повний очікуваний дохід
. З цього стану система здійснює решта n – 1 крок і отримує повний очікуваний дохід ![]() . Далі, повний очікуваний дохід за n кроків дорівнює
. Далі, повний очікуваний дохід за n кроків дорівнює ![]() , при умові, що перший крок перевів систему з стану і в стан j. [4]
, при умові, що перший крок перевів систему з стану і в стан j. [4]
За формулою
повного математичного сподівання отримаємо наступне рекурентне співвідношення:
![]() (5)
(5)
або
![]() , (6)
, (6)
де ![]() ,
, ![]() – продажна вартість системи, якщо вона закінчує функціонування в стані j,
– продажна вартість системи, якщо вона закінчує функціонування в стані j, ![]() – середній
однокроковий дохід, отриманий системою при переході зі стану і.
[3]
– середній
однокроковий дохід, отриманий системою при переході зі стану і.
[3]
Позначивши ![]() – вектор-стовпець
повного очікувано-го доходу,
– вектор-стовпець
повного очікувано-го доходу, ![]() – вектор-стовпець
середнього однокрокового доходу, запишемо формулу (6) у векторній формі.
– вектор-стовпець
середнього однокрокового доходу, запишемо формулу (6) у векторній формі.
![]() . (7)
. (7)
Враховуючи
переоцінку майбутнього доходу
![]() ,
,
отримаємо
![]() , (8)
, (8)
де ![]() - коефіцієнт переоцінки майбутніх
доходів,
- коефіцієнт переоцінки майбутніх
доходів, ![]() . [4]
. [4]
Якщо
використати формулу (8) n-разів при ![]() , отримаємо
, отримаємо
![]() . (9)
. (9)
Знайдемо
граничний дохід
![]() .
.
Нехай ![]() , тоді
, тоді ![]() , при
, при ![]() . Звідси отримаємо, що
. Звідси отримаємо, що
![]()
є скінченою величиною.
Нехай ![]() , тоді
, тоді 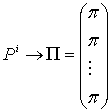 при
при ![]() , де
, де ![]() - матриця, рядки якої є сталими. Отже
- матриця, рядки якої є сталими. Отже ![]() .
.
Таким чином
граничний дохід при ![]() набуде наступного
вигляду:
набуде наступного
вигляду:
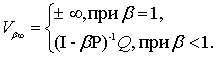 (10)
(10)
Список
використаних джерел
1.
Гихман И.И., Скороход
А.В., Ядренко М.И. Теория вероятностей и математическая статистика// Гихман И.И., Скороход А.В., Ядренко М.И. // - Киев: Наукова думка, 1978. – 583 с.
2.
Соколов Г.А., Чистякова Н.А. Управляемые
цепи Маркова в економике// Соколов Г.А., Чистякова Н.А// Теория вероятностей. М.: ФИЗМАТЛИТ, 2005.–248 с.
3.
Таха Х. Введение в исследование операций // Таха Х. - Т. 1, 2. –
М.: Мир, 1990. – 274 с.
4.
Ширяев А.Н. Вероятность //
Ширяев А.Н. – М.: Мир, 1989. – 378 с.