Математика/Прикладная математика
К.т.н.
Шотиков А.В.
Харьковский
национальный технический университет сельского хозяйства им. П. Василенко
АНАЛИТИЧЕСКИЕ АЛГОРИТМЫ ОТОБРАЖЕНИЯ ПРОСТРАНСТВА В СТЕРЕОПАНОРАМУ С
КОНИЧЕСКОЙ КАРТИННОЙ ПОВЕРХНОСТЬЮ
В работе [1] предложена модель отображения
пространства в стереопанораму, которая позволяет получать объёмные изображения
с любыми горизонтальными углами зрения без появления периферийных искажений и
вертикальных параллаксов. К недостаткам указанной модели следует отнести
сравнительно небольшой угол отображения в вертикальном направлении, так как
проецирование объекта производится на вертикальный цилиндр.
В практике проектирования площадей,
городских строений и т.п. иногда требуется получение изображений с большими горизонтальными
и вертикальными углами зрения, поэтому в таких случаях целесообразно
использовать в качестве картинной поверхности аппарата отображения конус.
Построение стереоскопических изображений
на коническую поверхность аналогично получению стереопанорамы на цилиндрическую
поверхность. Отличительной особенностью таких моделей является наличие в их
аппаратах дополнительной проецирующей связки полупрямых с центром в точке
отображения, что позволяет путём центрального проецирования преобразовать
стерео-панорамное изображение, полученное на цилиндрической поверхности, в
стерео-панорамное изображение на любую поверхность вращения с вертикальной
осью, проходящей через центр базисной окружности.
Рассмотрим алгоритмы такого
преобразования.
Проекции точки ![]() определяются
соответственно как результат
определяются
соответственно как результат
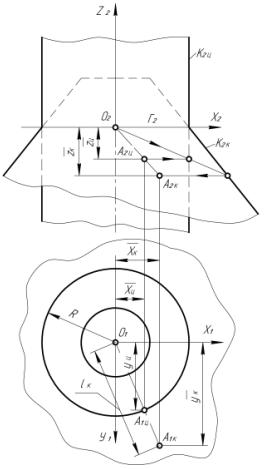
пересечения луча ![]() с конической поверхностью (рис. 1).
с конической поверхностью (рис. 1).
|
Рис. 1 |
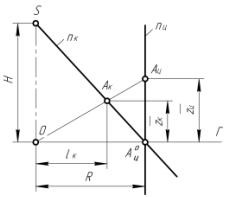
Рис. 2 Для упрощения формул отображения
пространства на коническую поверхность линия её пересечения с цилиндрической
картинной должна совпадать с плоскостью горизонта Из рис. 1 и рис. 2 вытекает следующая зависимость
между координатами точек на поверхностях отображения. |
![]() ;
; ![]() ;
; ![]() … , (1)
… , (1)
где ![]() ,
, ![]() ,
, ![]() - координаты точки
- координаты точки ![]() на цилиндрической
поверхности;
на цилиндрической
поверхности; ![]() ;
; ![]() ;
; ![]() - декартовы
координаты точек
- декартовы
координаты точек ![]() на конической поверхности;
на конической поверхности; ![]() - расстояние в плане до проекции
- расстояние в плане до проекции ![]() точки
точки ![]() от центра отображения
от центра отображения ![]() ;
; ![]() - радиус цилиндрической картины.
- радиус цилиндрической картины.
Определим аналитическую зависимость ![]() от
от ![]() . Для этого рассмотрим осевые
сечения аппаратов отображения (рис. 2).
. Для этого рассмотрим осевые
сечения аппаратов отображения (рис. 2).
Для конической поверхности из
треугольников ![]() и
и ![]() имеем:
имеем:
![]() , (2)
, (2)
где ![]() - высота вершины конуса относительно плоскости горизонта.
- высота вершины конуса относительно плоскости горизонта.
Подставив выражение (2) в (1), будем
иметь:
![]() ;
; ![]() ;
; ![]() (3)
(3)
Учитывая, что формулы отображения точек
пространства в стереопанораму на цилиндрическую картину ![]() ,
, ![]() ,
, ![]() имеют вид:
имеют вид:
![]() , (4)
, (4)
![]() , (5)
, (5)
![]() , (6)
, (6)
окончательно получим:
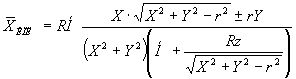 , (7)
, (7)
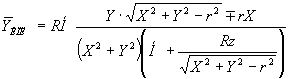 , (8)
, (8)
![]() , (9)
, (9)
в которых ![]() ,
, ![]() ,
,![]() - декартовы координаты стереопанорамных правых и левых
проекций точек объекта на конической поверхности (при этом для
- декартовы координаты стереопанорамных правых и левых
проекций точек объекта на конической поверхности (при этом для ![]() ,
, ![]() , в выражениях (7, 8) следует брать верхние знаки, а для
, в выражениях (7, 8) следует брать верхние знаки, а для ![]() ,
, ![]() , - нижние);
, - нижние); ![]() ,
, ![]() ,
, ![]() - декартовы координаты точек объекта;
- декартовы координаты точек объекта; ![]()
![]() - радиус базисной
окружности аппарата отображения.
- радиус базисной
окружности аппарата отображения.
Полученные формулы отображения
пространства в стереопанораму позволяют использовать ЭВМ для построения
объемных изображений на конической
картинной поверхности.
Литература:
1. А.В. Шотиков.
Стерео-панорамные изображения и способы их получения.//Автореферат канд. техн.
наук. – К. 1984г.