Развитие информационных технологий позволяет решать все более сложные задачи, к которым относится и задача эффективного запоминания и восстановления данных о любых объектах. Такая задача также подразумевает, что входящая информация об объекте может быть неполной или неточной.

Исследования в даной области могут привести к созданию универсального элемента памяти, обладающего свойствами, похожими на человеческую память. Это позволит эффективно решать задачи распознавания образов, поиска информации, строить экспертные системы и т.д.

Для решения задачи моделирования процессов памяти можно воспользоваться аппаратом нейронных сетей. Для этого следует построить структурную модель системы, состоящей из нейронных сетей, и математическую модель отдельного нейрона.

Структурное моделирование системы нейронных сетей базируется на физиологическом изучении человеческого мозга [1,2]. За основу берется кора головного мозга. Моделирование работы нейрона происходит либо при помощи функционального моделирования  – замены биологических нейронов их аналогами, построеными при помощи физических элементов [3], либо математического  моделирования, основанного на биологических исследованиях нейронов [4,5].

Представленная в данной статье структурная модель системы нейронных сетей является формализованой концептуальной моделью, состоящей из  распознавательной системы на основе колонок нейронов и системы знаний [1,2,6]. В статье вводится три свободных переменных для описания каждой колонки нейронов. На основе этих переменных описываются количество нейронов на каждом иерархическом уровне колонки и их связи друг с другом и  с  нейронами извне. В качестве системы знаний предлагаются две карты пар нейронов.

Математическая модель работы нейрона построена с использованием двух методов моделирования: функционального [3] и математического [4,5]. Это позволяет максимально использовать  преимущества каждого метода и ,  по возможности, избежать их недостатков.

Вначале опишем структурную модель системы. Для этого следует определить представление объектов, которые будет запоминать система,  ее основные компоненты и их структуру.

Любой входящий объект можно выразить в виде последовательности характеристик. При этом каждая характеристика тоже может быть объектом. Таким образом, объекты являются последовательностями последовательностей характеристик [6].

Очевидно, что система, которая сможет запоминать и распознавать такие объекты, должна иметь иерархическую структуру. В зависимости от сложности объекта, для его запоминания или определения понадобится элементы с более высокого уровня иерархии [1, 7]. Кроме того, такую систему можно разделить на две подсистемы: распознавательную и систему знаний.

Распознавательная система занимается тем, что обрабатывает входящую информацию об объектах, и либо записывает обработаные данные в систему знаний (процесс запоминания), либо определяет соответсвие данных одному из объектов в системе знаний (процесс распознавания).

Вначале рассмотрим распознавательную систему. Как было сказано выше, она является иерархической системой, состоящей из базовых элементов, – колонок нейронов. Каждая колонка находиться на одном уровне иерархии и связана только с колонками низшего и высшего уровней иерархии, а также с системой знаний. При этом каждая колонка тоже имеет иерархическую структуру, но при этой базовый элемент колонки – нейрон.

Каждую колонку можна охарактеризовать при помощи трех переменных:

N ­– количество характеристик, которые колонка получает на вход,

K – количество объектов, которые может запомнить колонка,

M определяет количество связей колноки с системой знаний, а также с колонками низшего уровня иерархии.

Каждая колонка имеет шесть уровней иерархии, которые можно пронумеровать сверху вниз. Так, первый уровень иерархии в колонке будет самым ближним к колонкам высшего уровня, в то время как шестой – ближним к колонкам низшего уровня.

Рассмотрим синапсы, приходящие от колонок низшего уровня иерархии. С их помощью осуществляется передача сигналов между нейронами. Синапсы попадают на четвертый уровень иерархии. Нейроны этого уровня определяют характеристики, которыми может оперировать колонка. Таким образом, на четвертом уровне иерархии будет находится N нейронов, никак не связаных между собой.

Второй и третий уровни иерархии колонки отвечают за определение объекта. Так если объект известен, то будут активированы нейроны второго уровня, если же нет – то третьего. При этом третий уровень иерахии состоит из пар нейронов: обычного и корзинчатого. Корзинчатый нейрон активируется только при известном объекте и не дает активироваться обычному нейрону.

Нейроны первого уровня в свою очередь отвечают за запомненные объекты. На основе представленых выше характеристик на первом уровне колонки будет нахоится K нейронов, при этом они все будут связаны между собой.

На втором уровне находится NK нейронов, а на третьем – NK пар нейронов. Каждый нейрон четвертого уровня связан с K нейронов второго уровня и K пар нейронов третьего. При этом нейроны и пары нейронов каждой из этих групп связаны между собой. Нейроны этих групп передают сигнал на нейроны первого уровня.

В свою очередь каждый нейрон первого уровня связан исходящими синапсами с N нейронами второго уровня и N пар нейронов третьего. Аналогично нейроны этих групп тоже связаны между собой. Нейроны второго и третьего уровней передают сигнал колонкам, стоящим на следующем уровне иерархии. Кроме этого, нейроны первого уровня передают сигнал нейронам пятого и шестого уровней иерархии. Для каждого из нейронов первого уровня существует группа из MN нейронов второго и тертьего уровня, которая получает от него сигналы. Нейроны этой группы связаны между собой.

Нейроны пятого и шестого уровня передают сигнал нейронам четвертого уровня иерархии. На каждый нейрон четвертого уровня приходится группа из MK связаных между собой нейронов. Таким образом можно сделать вывод, что на пятом и шестом уровнях иерархии находится MKN нейронов.

Кроме того, нейроны пятого и шестого уровней иерархии передают сигналы колонкам более низкого уровня иерархии, а нейроны шестого уровня иерархии тоже обмениваются сигналами с системой знаний.

Задав таким образом структурную модель распознавательной системы, опишем теперь систему знаний, поскольку распознавательная система неспособна полноценно хранить информацию об объектах.

Для системы знаний лучше всего выбирать систему из двух карт пар нейронов. Первая карта будет хранить в себе информацию обо всех известных объектах, вторая будет хранить информацию о классах объектов. Таким образом, во время процесса обучения при наборе достаточного количества подобных объектов система будет формировать соответсвующий класс. При этом каждая пара карты нейронов будет представлять собой обычный и корзинчатый нейрон. Каждая такая пара отвечает за отдельный объект, а наличие в паре корзинчатого нейрона позволяет реализовать механизм подавления активации соседних нейронов.

Для дальнейшего использования полученной системы следует описать поведение каждого нейрона. При этом следует учитывать, что в рассматриваемой ниже математической модели время – величина дискретная.

Как уже упоминалось, передача сигнала между нейронами осуществляется при помощи синапсов. Каждый нейрон во время активации генерирует потенциал действия, что приводит к выбросу порций нейромедиаторов, которые распространяются по синапсам. Нейромедиаторы, поступившие на вход к нейрону, вызывают у него изменения потенциала: увеличение (гиперполяризация) или уменьшение (деполяризация) в зависимости от типа нейромедиатора.

В состоянии покоя потенцил нейрона равняется . Для того, чтобы нейрон был активирован, требуется изменить потенциал нейрона на величину,  превышающую порог нейрона . При этом порог нейрона – это величина, зависящая от состояния нейрона, а также от времени пребывания нейрона в этом состоянии. Поэтому порог нейрона является функцией, зависящей от времени – .

Как было сказано выше, нейрон будет активирован, когда:

,

где  – изменение потенциала нейрона, представляющее собой переменную напряжения на емкости мембраны во время прохождения через нее синаптического тока  .

Такой ток описывается при помощи -функции [5], которая характеризирует резкий скачок постсинаптического потенциала после активации нейрона, а также его медленное угасание:

,                                                                 (1)

где  – максимальная синаптическая проводимость синаптического контакта в нейроне,

 – синаптический ток в момент генерации потенциала действия,

 – постоянная задержки, что характеризует время распространения нейромедиаторов в аксоне. В общем случае можно предположить, что

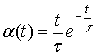,                                                                                 (2)

где  – постоянная, характеризующая синаптическое время – время дифузии нейромедиатора в синаптической щели от пресинаптической до постсинаптической мембраны

Теперь напишем уравнение для определения  [3,8]:

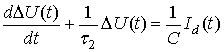,                                                       (3)

где  – постоянная времени мембраны,

,  – сопротивление и емкость мембраны соответственно.

Переменная  представляет собой время, прошедшее с начала запуска системы. Таким образом можно считать, что  . Решив уравнение (3) с учетом этого условия, получим следующее выражение :

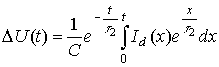                                                         (4)

Для более развернутого решения уравнения (4) воспользуемся уравнениями (1) и (2), описывающими синаптический ток :

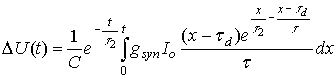
Решив это уравнение,  получаем

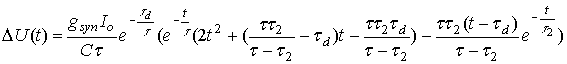
Полученная выше формула работает только для одного синапса. Для того, чтобы определить полное изменение потенциала нейрона, следует просуммировать полученые формулы с учетом каждого синапса:

,

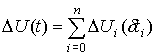где  – определяется для каждого -го синапса при помощи выведеной выше формулы,

 – время существования импульса до момента .

Таким образом нейрон будет активирован, когда:

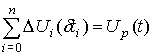
Как было сказано выше, активация нейрона приводит к генерации потенциала действия, а также передаче синаптического тока, который ведет ко всем привязаным нейронам.

Сразу после активации нейрон переходит в состояние абсолютной рефактерности. В таком состоянии нейрон не может быть активирован вообще.

Из состояния абсолютной рефактерности нейрон переходит в состояние относительной рефактерности. В этом состоянии порог нейрона экспоненциально уменьшается от очень высокого до порога в состоянии покоя. Как только период относительной рефактерности заканчивается, нейрон попадает в состояние покоя.

Изменение порога нейрона в состоянии относительной рефактерности можно описать следующим образом:

,

где  – постоянная, характеризующая продолжительность периода относительной рефактерности,

 – величина порога нейрона в начале периода относительной рефактерности,

 – порог нейрона в состоянии покоя.

В данном случае точкой отсчета времени считается начало периода относительной рефактерности.

В момент активации нейрона происходит генерация потенциала действия и передача синаптического тока другим нейронам. Для определения этого тока следует воспользоваться моделью Ходжкина-Хаксли [4].

Ионный ток, проходящий через мембрану, представляет собой сумму трех ионных токов: натриевого , калиевого  и тока других ионов :

                                                                        (5)

Все эти три тока можна описать в треминах ионной проводимости:

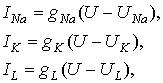                                                                    (6)

где , ,  – равновесный натриевый, калиевый и другой ионный потенциалы соответсвенно,

 – потенциал мембраны в данный момент времени.

Функции , ,  отвечают за ионную проводимость нейрона. Их можна выразить при помощи уравнений четвертого порядка:

,                                                                             (7)

,                                                                                  (8)

,                                                                                      (9)

где , ,  – константы, означающие максимально возможную  проводимость ионов натрия, калия и других соответсвенно.

Так же можно описать зависимости функци m, n, h от времени:

,

,

Коэфициенты , , , , ,  имеют размерность  и выражаются следующим образом [7]:

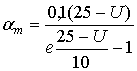,                                                                         (10)

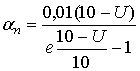,                                                                        (11)

,                                                                              (12)

,                                                                                  (13)

,                                                                             (14)

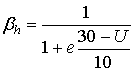                                                                          (15)

Следует отметить, что в формулах (10)-(15) используется размерность  равная . Таким образом описывается динамика изменения ионной проводимости нейрона в зависимости от времени. Для этого подставим (6)-(9) в (5):

Теперь можно определить ток, который будет передаваться через синапсы другим нейронам в момент генерации потенциала действия:

,

где  – общий синаптический ток, представляющий собой сумму всех отдельных синаптических токов, описаных в (1).

Даные формулы представляют собой математическую модель нейрона. Они описывают передачу импульса между нейронами, процесс изменения порога нейрона в зависимости от его состояния, процесс изменения потенциала нейрона, а  также  ток, который передается по синапсам в момент генерации потенциала действия – активации нейрона.

Используя даную математическую модель совместно с представленой выше структурной моделью, можно создать дискретную систему, состоящую из нейронных сетей, которая позволит решать задачи запоминания и распознавания различных образов, предварительно закодированых в виде электрических сигналов. Дальнейшие исследования этой системы предполагают построение компьютерной модели, которая может быть использована как универсальный элемент памяти в различных поисковых системах, экспертных системах и т.д. А более глубокое  исследование  свойтсв  такой системы позволит вывести универсальные законы, на которые можно будет опиратся при ее применении в описаных выше областях. Кроме того, такое соответствие представленой модели процессам, которые происходят в памяти человека, позволяет сказать, что при более детальном изучении ее свойств можно будет получить более четкое представление о таких вещах как интеллект, мышление, память и т.д.

 

Список использованой литературы.

 

1.          Эдельман Дж. Разумный мозг / Джеральд Эдельман, Вернон Маунткастл. – М. : Мир, 1981. – 135 с.

2.          Хьюбел Д. Глаз, мозг, зрение / Дэвид Хьюбел. – М. : Мир, 1990. – 240 с.

3.          Познин Н.В. Моделирование нейронных структур / Н.В. Познин – М.: Наука, 1970. – 260 с. : ил.

4.          Ходжкин А. Нервный импульс. Пер. с англ. / А. Ходжкин. – М.: Мир, 1965. – 125 с.

5.          Hastings A., Higgins K. Persistence of transients in spatially structured ecological models / A. Hastings, K. Higgins // Science. – 1994. – Vol. 263. – P. 1133-1136.

6.          Хоккинс Дж. Об интеллекте / Джефф Хоккинс, Сандра Блейксли. – М. : Вильямс, 2004. – 240 с.

7.          Потієнко М.В. Ієрархічна структура нейронної мережі пам’яті людини / М.В. Потієнко // Матеріали 12-ї Міжнародної науково-технічної конференції Системний аналіз та інформаційні технології. – 2010. – С. 302

8.          Потиенко М.В. Математическая модель нейрона памяти человека / М.В. Потиенко // Труды XI международной научно-практической конференции Современные информационные и электронные технологии, том I. – 2010. – С. 27