УДК 622.83

Помашев О.П.

О НАПРЯЖЕНИЙ ВЕРХНИХ СЛОЕВ ПОРОД ЗЕМНОЙ КОРЫ

При радиусе земного шара R и текущем изменяющемся радиусе r от центра Земли до некоторой точки коры, давление деиствующее на глубине можно записать в виде

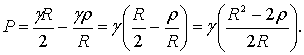(1)

Горизонтальное напряжение σ_θ , действующее в горных породах, можно записать

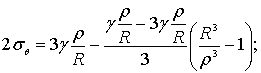
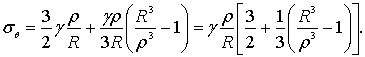(2)

В расчетах, естественно, (ρ/R)<1 , но приблизительно при малых глубинах Н по сравнению с земным радусом R= 6370км, отношение можно принять равным еденице, т.е. , в следующих выражениях:

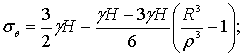
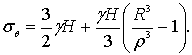`(3)

При вычислении значения второго члена уравнения (3) на глубине Н равном 2, 10 и 1000км, соответственно получены величины: ≈0; ≈0,4 и 6156,2 МПа. Эти вычисления значений второго члена уравнения (3) дают основание полагать, что при малых глубинах Н можно записать выражение

(4)

которое можно считать основной расчетной формулой горизонтальных напряжений в земной коре при малых глубинах Н проведения горных выработок.

Опираясь на приближенные расчетные схемы напряжений в земной коре автора [1], можно вывод формулы развивать еще следующим образом:

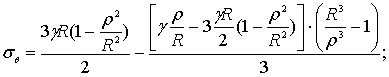
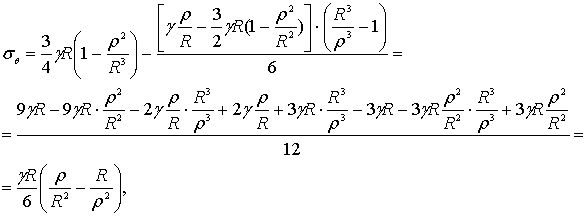
(5)

ввиду того, что при малых глубинах R ≈ p .

Были рассчитаны напряжения в земной коре при изменении глубины до 1000м с шагом расчета через 50 и 100м, также для глубины 10⁶м. Эти результаты расчетов сведены в таблицу 1.

Так же была опробирована полученная нами расчетная формула напряжения б_θ следующего вида:

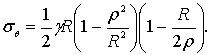(6)

Рассчитанное по формуле (6) значение горизонтального напряжения б_θ на глубине 370км, т.е. при р=6000км. равно ≈4630МПа. На этой же глубине значение давления γH вдоль радиуса земли, вычисленное для сравнения с б_θ, составляет 10212 МПа.

Расчеты показывают, что с глубиной напряженное состояние горных пород земной коры увеличивается. Если для средней б_θ до глубины 1000м (см. таблицу 1) составляет 18271 МПа со средним градиентом изменения б_θ, на этом интервале 0,0054 (0,54%), то аналогичные величины для γH на этом же интервале глубины до 1000м составляют γH =755МПа, а средний градиент -0,241 (24,15%). Это связано с действием силы тяготения к центру земли. Более стабильный характер горизонтального напряжения с глубиной, по-видимому, связано со стабильно установившимся вращением Земли вокруг своей оси, при которой экваториальная точка на поверхности имеет линейную скорость порядка:

(7)

Таблица 1. – Сводные результаты расчетов напряжений в земной коре.

№ п/п	Глубина Н, м.	γH,МПа	γH, МПа	Напряжения, Мпа
				бθ по формуле Нореля	бR, радиальная
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.	50 100 150 200 250 300 350 400 500 600 1000	1,38 2,76 4,14 5,52 6,90 8,28 9,66 11,04 13,80 16,56 27,50	2,07 4,14 6,21 8,28 10,35 12,42 14,49 16,56 20,70 24,84 41,40	20093,5 20094,3 20095,0 20095,8 20096,5 20097,3 20098,0 20098,8 20100,3 20101,8 20107,8	1,07 2,13 3,19 4,26 5,32 6,39 7,45 8,52 10,65 12,77 21,29
12.	10^6	27600,0	41400,0	33899,9	1884324

Горные породы верхних слоев Земли, до глубины 1000 и более метров, находясь под влиянием такой установившейся скорости 463м/с, направленной с Запада на Восток перпендикулярно к радиусу Земли, должны выдерживать примерно одинаковый горизонтальный боковой распор, что видно из таблицы 1. И поэтому в таблице 1 значения напряжения б_θ при малых глубинах весьма мало изменяются, остоваясь почти постоянными по сравнению со значениями б_R, направленной вдоль радиуса к центру Земли.

Литература

1. Норель Б.К. Приближенное определение напряжений на поверхности земли от действия гравитационных сил., «Научные сообщения»ИГД им. А.А.Скочинского, 1970, №74, стр.86-89.