Достиярова А. М. - к.т.н., доцент КазАТК им.М.Тынышпаева

метод анализа нестационарных сигналов

Основные свойства, которыми должны обладать весовые функции Н(п) являются следующие [1]:

- ширина главного лепестка частотной характеристики , содержащего по возможности большую часть общей энергии;

- энергия боковых лепестков должна быстро уменьшаться при приближении к значению

Таким образом, для построения дискретного фильтра необходима априорная информация как о полосе занимаемых частот полезного сигнала и шума, так и о свойствах синтезируемого фильтра - требование к фильтру во временной и частотной области.

Частным случаем ДПФ является дискретно-косинусное преобразование Фурье (ДКП), которое задается парой преобразования:

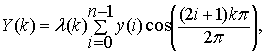(1)

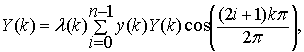(2)

где - совокупность весовых функций:

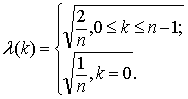
(3)

Широко исследуется метод анализа нестационарных сигналов на основе главных компонент - метод «Гусеница» (SSA или Singular Spectrum Analisys) [2]. Преобразование одномерного временного ряда в многомерный осуществляется путем скользящего разбиения исходной реализации на перекрывающиеся интервалы одинаковой длины («длина гусеницы») и записи реализации в виде матрицы размера , где N - длина исходной реализации, а М - длина интервала разбиения [2]:

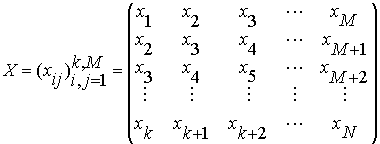, (4)

где - исходные значения анализируемого процесса.

По полученной матрице X вычисляется матрица [23]

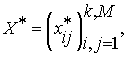(5)

где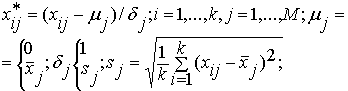

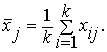Затем вычисляется выборочная корреляционная матрица R:

(6)

С элементами 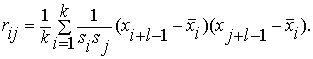Последующее сингулярное разложение матрицы R имеет вид [23]:

(7)

где - диагональная матрица собственных чисел, а Р - ортогональная матрица собственных векторов матрицы R, при этом выполняются следующие соотношения:

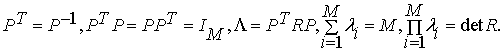
Полученное преобразование очень близко к линейному преобразованию исходного сигнала с помощью дискретного оператора свертки, т.е. [2]:

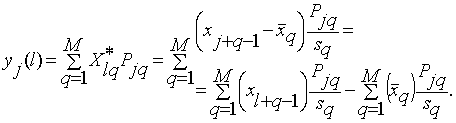
(8)

Следовательно, процедура "Гусеница" порождает набор линейных фильтров, настроенных на составляющие исходного процесса. При этом собственные векторы матрицы R выступают в роли переходных функций соответствующих фильтров. После отбора главных компонент, т.е. выбора некоторого количества r главных компонент с номерами осуществляется восстановление многомерного ряда [2]:

(9)

В случае необходимости, производится децентрирование и денормирование матрицы в результате получают матрицу Завершающим этапом является ганкелизация, т.е. восстановление одномерного ряда путем усреднения по побочным диагоналям [2]:

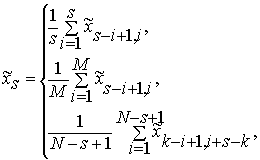
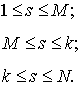(10)

Следует отметить, что метод "гусеницы" имеет ряд достаточно важных преимуществ перед вейвлет-анализом [2], заключающийся в том, что набор базисных функций порождается самим исследуемым сигналам. Несмотря на это, авторами не даны четкие рекомендации по правилу выбора составляющих разлагаемого сигнала, их количеству.

ЛИТЕРАТУРА

1.Основы цифровой обработки сигналов. А.И.Солонина, Д.А.Улахович, С.М.Арбузов, Е.Б.Соловьева/ Изд. 2-е испр. и перераб.-СПб.: БХВ-Петербург, 2005.-768с.

2. Данилов Д.Л., Жиглявский А.А. (ред.) Главные компоненты временных рядов: Метод «Гусеница». Санкт-Петербург, Санкт-Петербургский государственный университет, 1997.-308с.