Современные информационные технологии/ 1. Компьютерная  инженерия

д.т.н., проф. Сербулов Ю.С., к.т.н., доц. Сысоев Д.В., к.т.н. Курипта О.В.

Воронежская государственная лесотехническая академия, Россия

Воронежский государственный архитектурно-строительный университет, Россия

Моделирование информационных процессов взаимодействия конкурирующих систем в условиях рынка

Целью исследования является построение математической модели ресурсного взаимодействия конкурирующих систем в рыночных отношениях, позволяющей определить основные характеристики этого процесса.

В настоящее время установлено [1], что чаще всего причиной возникновения конкуренции является общий ресурс, поэтому конкуренция может возникать даже на ранних этапах взаимодействия и приводить к появлению на рынке качественно нового пула конкурирующих за общий ресурс систем. Развитие этих автономных систем до некоторого момента времени характеризуется экспоненциальным ростом с неменяющимися показателями.

Обозначим через потенциал системы А₂ в момент времени t через x(t), тогда рост потенциала в условиях неограниченного на рынке ресурса может быть описан формулой:

, (1)

где x(0) – потенциал системы А₂ в начальный момент времени, т. е. в момент t₀ – момент появления системы А₂ на рынке; величина α – коэффициент пропорциональности, который назовем удельной скоростью изменения потенциала α = μ₂-c₂, где μ₂ и c₂ – коэффициенты, характеризующие удельные скорости роста потенциала соответственно в период развития и стагнации системы А₂.

Аналогично запишем формулу развития системы А₁:

, (2)

где y(0) – потенциал системы А₁ в начальный момент времени, т. е. в момент t₀ – момент появления на рынке конкурирующей системы А₂; величина β = μ₁-c₁, где μ₁ и c₁ – коэффициенты, характеризующие удельные скорости роста (убывания) потенциала соответственно в периоды развития и стагнации системы А₁.

Характерной особенностью обеих систем является их способность к самоподдержанию. Благодаря этому свойству обеспечивается некоторое равновесие систем на рынке, несмотря на конкурирующий вид взаимодействия.

После своего образования обе системы начинают свободно развиваться. Пока их потенциал остаётся низким, а взаимодействие между ними слабым, этот рост будем считать экспоненциальным. На поздних стадиях процесса развития систем, когда относительный объем потенциалов обеих систем на рынке значительно увеличивается, наступает замедление экспоненциального роста, вызванное эффектом «перенаселения».

Характерной особенностью конкуренции является резкое подавление одной системы нормального функционирования другой системы. Причина этого нарушения до настоящего времени является малоизученной. Можно сделать предположение, что система А₂ обладает способностью подавлять дифференциацию развития системы А₁.

Рассмотрим упрощенную модель ресурсного взаимодействия конкурирующих систем, когда блокировка развития системы А₁ наступает после того, как конкурирующая система А₂ достигает некоторого критического этапа развития с точки зрения заданного бесконфликтного с системой А₁ взаимодействия [2]. Момент, когда происходит резкий перелом в ходе кривой процента занятого на рынке объема системой А₁, можно интерпретировать как начало резкого ухудшения ее взаимодействия с системой А₂. Отсутствие экспериментальных данных по течению процесса не позволяет определить этот момент точно.

В первом приближении будем предполагать, что действие системы А₂ на систему А₁ на качество их взаимодействия носит пороговый характер, т.е. резкое ухудшение качества взаимодействия начинается в некоторый момент времени t_порог при достижении системой А₂ некоторого потенциала, который назовем критическим для системы А₁ потенциалом и обозначаемым x_кр. Система А₁ остается как бы заторможенной при . Если х(t) с некоторого момента времени становится меньше x_кр, например, после воздействия системы А₁ на систему А₂ путем внесения в процесс взаимодействия некоторого действия, то система А₁ начинает, развиваясь, повышать качество на рынке своего функционирования. Это продолжается до момента достижения системой А₂ потенциала x_кр и т.д. Конечно, предлагаемый принцип лишь приближенно описывает процесс воздействия системы А₂ на систему А₁.

Однако, принцип порогового действия позволяет описать ресурсное взаимодействие конкурирующих систем А₁ и А₂ с помощью одного параметра x_кр. Всякое усложнение представления о взаимодействии фактически приводит к увеличению числа параметров, что существенно снижает ценность модели ввиду отсутствия достаточного количества статистических данных.

Рассмотрим примеры возможного взаимодействия в пуле конкурирующих систем в момент времени _, потенциал системы А₁ до этого момента будем считать равным y_const.

Обозначим потенциал системы А₁ в момент времени через , где t_разв - время развития системы А₂. Здесь под понимается потенциал системы А₁ в момент времени Т_норм, оказывающих влияние на увеличение показателей качества своего развития. Потенциал еще некоторое время будет оставаться равным у_const. Это время равно времени развития систем t_разв. Но при потенциал системы А₁ начинает убывать, так как к этому времени начинает сказываться развитие системы А₂, вызванной ростом её потенциала.

Можно предположить, что потенциал системы А₁ по степени влияния на качество бесконфликтного взаимодействия с системой А₂ за время после момента можно определить по соотношению .

Здесь величина β характеризует скорость убывания воздействия на качество своего положения на рынке системы А₁.

Разрешая данное уравнение при начальных условиях ,, получаем , .

Тогда график изменения можно представить в виде рис.1.

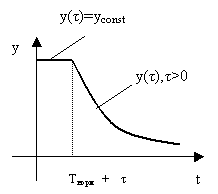
Рис. 1. График изменения потенциала системы А₁ в процессе развития конкуренции

Рассмотрим теперь взаимоотношения между системами А₁ и А₂ в далеко зашедшей стадии развития конкуренции, когда в результате «эффекта перенаселения» наступает замедление экспоненциального роста обеих систем. Обозначим момент времени замедления роста . Поскольку механизмы этих явлений остаются неизученными, введем гипотетическое предположение, заключающееся в том, что на данной стадии воздействия конкуренции скорость роста потенциала системы А₂ не должна превышать скорость роста потенциала системы А₁ . Тогда

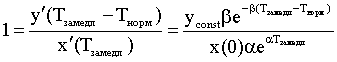. (3)

Из этого уравнения получаем соотношение потенциалов и x(t) в момент времени Т_замедл. Имеем:

,

. (4)

Все вышеизложенное позволяет охарактеризовать влияние конкуренции от момента появления первых на рынке – t_0, когда потенциал системы А₂ , до времени – момента полного отсутствия конкуренции. Предположим, что , а влияние контаминации происходит на отрезке времени .

В соответствии с изложенными представлениями этот отрезок времени может быть разбит на 4 этапа, соответствующих различным фазам, характеризующим состояние систем при конкуренции.

1. Фаза свободного развития системы А₂ от 0 до t_порог, т.е. до момента достижения системой А₂ потенциала x_кр. Как было показано выше, потенциалы систем А₁ и А₂ в период от 0 до t_порог соответственно равны и . Отсюда можно определить процент потенциала системы А₂ на рынке в этой фазе:

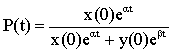, . (5)

2. Фаза начала воздействия системой А₂ на характер взаимодействия с системой А₁. Эта фаза начинается в момент t_порог и длится в течение периода t_раз – времени развития системы А₂ до момента _. В этот момент потенциал системы А₁ увеличивается. Процент потенциала системы А₁ также вычисляется по формуле (5), только .

3. Фаза выраженной конкуренции. В этой фазе потенциал системы А₁, определяющий качество взаимодействия с системой А₂, начинает убывать по экспоненте. Фаза длится от Т_норм до Т_замедл. В момент Т_замедл скорость роста потенциала системы А₂ достигает скорости роста потенциала систем А₁. Процент потенциала конкурирующей системы на рынке может быть вычислен по формуле:

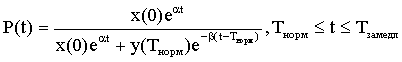. (6)

Заметим, что в этот период величина Р(t) резко увеличивается по сравнению с первой и второй фазами , т.к. начинает убывать по экспоненте при .

4. Фаза уменьшения скорости роста потенциала системы А₂. Эта фаза длится от Т_замедл до Т – момента времени полной потери устойчивого взаимодействия с системой А₁. Процент потенциала на рынке системы А₂ в этой фазе выражается формулой:

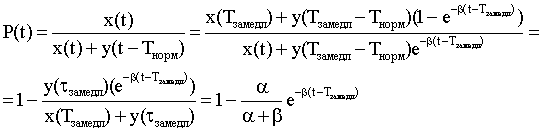, (7)

. (8)

Выражение для Р(t) в каждой фазе конкуренции дают возможность построить кривую Р(t) на протяжении всего развития и вычислить ее характерные точки через основные параметры (рис.2).

Первые две фазы, т.е. от 0 до Т_норм описываются одной функциональной зависимостью (5). При малом отношении , что с физической точки зрения вполне естественно, величина , но все же величина Р(t) идет более полого, чем , так как из (5) следует , что . Величина Р(t), достигая при Т_норм значения, приблизительно равного , затем ускоряет рост, принимает при Т_замедл значение и далее продолжает развиваться, постепенно замедляясь без точек перегиба. При этом в точке Т_замедл излома у соединяющихся участков кривой, заданных уравнениями (6) и (7), не будет, т.к. точка Т_замедл определяется из условия, что производные в ней у кривых (7) и (8) совпадают. Таким образом, кривая, описывающая процент потенциала системы А₂, будет иметь вид как на (рис.2).

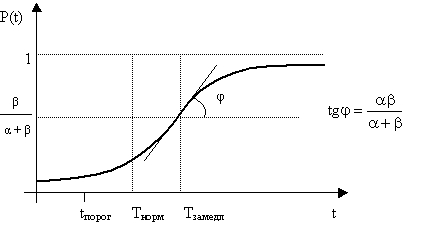
Рис.2. График изменения процента потенциала системы А₂ в процессе развития конкуренции

Пример. Данные, характеризующие изменение процента потенциала системы А₂ на рынке, приведены в таблице 1. (примечание: размеренность времени – виртуальная)

Таблица 1

Результаты расчета

Время	0	35	59	80	100
Р(t)*100%	3	5,1	9,5	51	56

Точка Т_замедл характеризуется тем, что и , так что . Это соотношение в принципе дает возможность по определить Т_замедл. Вычисления, проведенные на основе данных таблицы 1, дают значение и времени. Величина , определяемая по кривой Р(t) на участке, соответствующем фазе 3, оказывается равной 0,2. Момент Т_замедл можно определить из уравнения (7) при известных , и . Последнее определяется на данных таблицы 1 путем интерполирования к нулю. Отсюда получается . Так как , то . Это означает, что «эффект перенаселения» начинает сказываться примерно через 90 условных единиц времени после обнаружения на рынке системой А₁ системы А₂ . В соответствии с формулой (7) доля потенциала системы А₂ на рынке в момент «перенаселения» достигает 90%.

Список литературы:

1. Сербулов Ю.С. Модель конфликтно-устойчивого ресурсного взаимодействия производственно-экономических систем с внешней средой / Ю.С. Сербулов, Л.Е.Мистров, Д.В.Сысоев, Н.В.Сысоева. – Воронеж: Научная книга, 2008. – 270 с.

2. Сысоев Д.В. Автоматизированная процедура бесконфликтных операций управления поведением производственно-экономических систем в рыночных условиях / Д.В.Сысоев, Н.В.Сысоева // Вестник Воронежского института высоких технологий. – Воронеж: Научная книга, 2007, №2. – с. 224-227.