Математика/1.Дифференциальные и интегральные уравнения
Д.ф.-м.н. Городецький
В. В., к.ф.-м.н. Мартинюк О. В.
Чернівецький
національний університет імені Юрія Федьковича,Україна
Задача Коші для еволюційних рівнянь
із псевдодиференціальними
операторами
Еволюційні рівняння параболічного
типу з оператором Бесселя відносяться до рівнянь з виродженим за просторовими
змінними оператором (такі рівняння вироджуються на межі області) і за
внутрішніми властивостями вони близькі до рівномірно параболічних рівнянь.
Оскільки оператор Бесселя 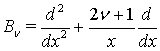 ,
, ![]() , можна визначити за допомогою співвідношення
, можна визначити за допомогою співвідношення ![]() , де
, де ![]() ,
, ![]() – пряме та обернене перетворення
Бесселя,
– пряме та обернене перетворення
Бесселя, ![]() – елемент простору, в
якому вказане перетворення визначене, то еволюційні рівняння з оператором
Бесселя природно віднести до псевдодиференціальних рівнянь. До такого ж класу
рівнянь слід віднести і еволюційні рівняння з псевдо-Бесселевим оператором
– елемент простору, в
якому вказане перетворення визначене, то еволюційні рівняння з оператором
Бесселя природно віднести до псевдодиференціальних рівнянь. До такого ж класу
рівнянь слід віднести і еволюційні рівняння з псевдо-Бесселевим оператором ![]() , де
, де ![]() є однорідним, негладким
у точці
є однорідним, негладким
у точці ![]() символом. Для
еволюційних рівнянь з псевдо-Бесселевими операторами з гладкими символами
задача Коші вивчалася в роботах Я.І. Житомирського [1], М.І. Матійчука, В.В.
Крехівського [2], С.Д. Івасишена, В.П. Лавренчука [3], В.В. Городецького [4], О.М.
Ленюка, Я.М. Дріня [5] та ін. Отримано вагомі результати стосовно коректності
задачі Коші та властивостей розв’язків.
символом. Для
еволюційних рівнянь з псевдо-Бесселевими операторами з гладкими символами
задача Коші вивчалася в роботах Я.І. Житомирського [1], М.І. Матійчука, В.В.
Крехівського [2], С.Д. Івасишена, В.П. Лавренчука [3], В.В. Городецького [4], О.М.
Ленюка, Я.М. Дріня [5] та ін. Отримано вагомі результати стосовно коректності
задачі Коші та властивостей розв’язків.
У той же час еволюційні рівняння з
псевдо-Бесселевими операторами, побудованими за однорідними, негладкими у
фіксованій точці символами на теперішній час досліджені не достатньо повно. У
даній роботі будуються нові класи псевдодиференціальних операторів, які містять
у собі клас псевдо-Бесселевих операторів, побудованих за сталими символами.
Розвивається теорія задачі Коші для еволюційних рівнянь з такими операторами та
початковими даними з просторів узагальнених функцій типу розподілів.
1. Простори основних та узагальнених функцій. Нехай ![]() ,
, ![]() :
: ![]() – неперервні, парні
на
– неперервні, парні
на ![]() функції,
диференційовні, монотонно зростаючі й необмежені на
функції,
диференційовні, монотонно зростаючі й необмежені на ![]() ,
, ![]() , причому функція
, причому функція ![]() опукла (донизу) на
опукла (донизу) на ![]() , тобто: а)
, тобто: а) ![]() :
: ![]() ; б)
; б) ![]()
![]() :
: ![]() ; в)
; в) ![]()
![]() :
: ![]() . Припускаємо, що виконуються наступні умови:
. Припускаємо, що виконуються наступні умови: ![]()
![]()
![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , де
, де ![]() та
та ![]() – фіксовані
параметри.
– фіксовані
параметри.
Символом ![]() позначимо сукупність
усіх неперервних, парних на
позначимо сукупність
усіх неперервних, парних на ![]() функцій
функцій ![]() :
: ![]() , нескінченно диференційовних на
, нескінченно диференційовних на ![]() , для яких
, для яких
![]()
(якщо ![]() , то сума відсутня, якщо
, то сума відсутня, якщо ![]() , то
, то ![]() і т.д.; якщо
і т.д.; якщо ![]() , то вказана нерівність справджується для всіх
, то вказана нерівність справджується для всіх ![]() ).
).
Нехай ![]() – фіксоване число з
множини
– фіксоване число з
множини ![]() . На функціях з простору
. На функціях з простору ![]() визначене
перетворення Бесселя
визначене
перетворення Бесселя ![]() [6]:
[6]:
![]() де
де ![]() – нормована функція
Бесселя;
– нормована функція
Бесселя; ![]() – парна на
– парна на ![]() функція і
функція і ![]() .
.
Нехай ![]() . Введемо в
. Введемо в ![]() структуру
зліченно-нормованого простору за допомогою норм
структуру
зліченно-нормованого простору за допомогою норм
![]() ,
, ![]()
де ![]() ,
, ![]() ,
, ![]() ,
, ![]() – фіксований
параметр. Збіжність у просторі
– фіксований
параметр. Збіжність у просторі ![]() – це збіжність за
кожною нормою
– це збіжність за
кожною нормою ![]() ,
, ![]() .
.
Перетворення Бесселя неперервно відображає ![]() на простір
на простір ![]() .
.
У
просторі ![]() визначений і
неперервний оператор узагальненого зсуву аргументу
визначений і
неперервний оператор узагальненого зсуву аргументу ![]() , який відповідає оператору Бесселя [6].
, який відповідає оператору Бесселя [6].
Символом ![]() позначатимемо простір
усіх лінійних неперервних функціоналів над відповідним простором основних
функцій зі слабкою збіжністю, а його елементи називатимемо узагальненими
функціями.
позначатимемо простір
усіх лінійних неперервних функціоналів над відповідним простором основних
функцій зі слабкою збіжністю, а його елементи називатимемо узагальненими
функціями.
Оскільки в просторі ![]() визначена операція
узагальненого зсуву аргументу, то згортку узагальненої функції
визначена операція
узагальненого зсуву аргументу, то згортку узагальненої функції ![]() з основною функцією
задамо формулою
з основною функцією
задамо формулою ![]() ,
, ![]() , при цьому
, при цьому ![]() для довільної
основної функції
для довільної
основної функції ![]() .
.
Нехай ![]() . Якщо
. Якщо ![]() ,
, ![]() , і із співвідношення
, і із співвідношення ![]() при
при ![]() за топологією
простору
за топологією
простору ![]() випливає, що
випливає, що ![]() при
при ![]() за топологією
простору
за топологією
простору ![]() , то функціонал
, то функціонал ![]() називається
згортувачем у просторі
називається
згортувачем у просторі ![]() .
.
Перетворення Бесселя узагальненої
функції ![]() визначимо за
допомогою співвідношення
визначимо за
допомогою співвідношення ![]() ,
, ![]() ,
, ![]() . З властивостей лінійності і неперервності функціоналу
. З властивостей лінійності і неперервності функціоналу ![]() та перетворення
Бесселя випливає лінійність і неперервність функціоналу
та перетворення
Бесселя випливає лінійність і неперервність функціоналу ![]() , заданого на просторі
, заданого на просторі ![]() . Отже,
. Отже, ![]() .
.
2. Задача Коші. Нехай ![]() :
: ![]() – неперервна, парна
на
– неперервна, парна
на ![]() функція, однорідна
порядку
функція, однорідна
порядку ![]() , нескінченно диференційовна на
, нескінченно диференційовна на ![]() , похідні якої задовольняють умову:
, похідні якої задовольняють умову:
![]() (1)
(1)
З (1) випливає, що функція ![]() є мультиплікатором у
просторі
є мультиплікатором у
просторі ![]() . У зв’язку з цим розглянемо оператор
. У зв’язку з цим розглянемо оператор ![]() :
: ![]() , який визначимо за допомогою співвідношення
, який визначимо за допомогою співвідношення ![]() ,
, ![]() (тут
(тут ![]() – обернене
перетворення Бесселя, яке неперервно відображає
– обернене
перетворення Бесселя, яке неперервно відображає ![]() на
на ![]() ). Із властивостей перетворення Бесселя (прямого й
оберненого) випливає, що
). Із властивостей перетворення Бесселя (прямого й
оберненого) випливає, що ![]() – лінійний і
неперервний псевдо-Бесселевий оператор.
– лінійний і
неперервний псевдо-Бесселевий оператор.
Розглянемо еволюційне рівняння з
оператором ![]() вигляду
вигляду
![]() (2)
(2)
де ![]() :
: ![]() – неперервна функція,
інтегровна на
– неперервна функція,
інтегровна на ![]() .
.
Під
розв’язком рівняння (2) розумітимемо функцію ![]() , яка задовольняє це рівняння.
, яка задовольняє це рівняння.
Фундаментальним розв’язком
рівняння (2) є функція ![]() ,
, ![]() , де
, де ![]() .
.
Символом ![]() позначимо сукупність
узагальнених функцій з простору
позначимо сукупність
узагальнених функцій з простору ![]() , які є згортувачами в просторі
, які є згортувачами в просторі ![]() .
.
Нехай ![]() . Тоді 1) у
просторі
. Тоді 1) у
просторі ![]() справджується
граничне співвідношення
справджується
граничне співвідношення ![]() ,
, ![]() ; 2) функція
; 2) функція ![]() ,
, ![]() , є розв’язком рівняння (2). Тоді задачу Коші для рівняння
(2) можна ставити так: знайти розв’язок
, є розв’язком рівняння (2). Тоді задачу Коші для рівняння
(2) можна ставити так: знайти розв’язок ![]() рівняння (2), який
задовольняє початкову умову
рівняння (2), який
задовольняє початкову умову
![]() (3)
(3)
в тому сенсі, що ![]() при
при ![]() у просторі
у просторі ![]() .
.
Теорема 3. Задача Коші (2), (3) є коректно розв’язною. Розв’язок подається у
вигляді згортки: ![]() ,
, ![]() , де
, де ![]() – фундаментальний
розв’язок рівняння (2).
– фундаментальний
розв’язок рівняння (2).
Література:
1.
Житомирский
Я. И. Задача Коши для систем линейных уравнений в частных производных с
дифференциальным оператором Бесселя // Матем. сб. – 1955. – Т. 36, №2. – С.
299-310.
2.
Крехивский
В. В., Матийчук М. И. Фундаментальные решения и задача Коши для линейных
параболических систем с оператором Бесселя // Докл. АН СССР. – 1968. – Т. 181,
№6. – С. 1320-1323.
3.
Ивасишен
С. Д., Лавренчук В. П. Об интегральном представлении решений параболической
системы с оператором Бесселя // Нелинейные граничные задачи. – 1992. – Вып. 4.
– С. 19-25.
4.
Городецький В. В.,
Ленюк О. М. Еволюційні рівняння з псевдо-Бесселевими операторами // Доп. НАН
України. – 2007. – №8. – С.11-15.
5.
Дрінь Я. М. Вивчення одного класу параболічних
псевдодиференціальних операторів у просторах гельдерових функцій // Доп. АН
УРСР. Сер. А. – 1974. – № 1. – С. 19-21.
6.
Левитан Б. И. Разложение по функциям Бесселя в ряды и
интегралы Фурье // Успехи мат. наук. – 1951. – Т. 6, вып. 2. – С. 102-143.