Ибрагимов У.М., Сарыпбекова Г.У., Баймишева А.Ж.

Южно-Казахстанский государственный университет им.М.Ауезова,

Южно-Казахстанский государственный педагогический институт

Задача синтеза в линейных управляемых системах

Введение. Задача синтеза оптимального управления заключается в нахождении функции синтеза, которая описывает зависимость управления от состояния управляемой системы. Значение функции синтеза можно вычислить, если решить задачу оптимального управления для текущей состояний, считая его начальным состоянием системы. В этом случае необходимо решать задачу оптимального управления непосредственно в процессе управления системой. Во многих случаях при управлении динамическими системами такая возможность отсутствует. Поэтому возникает проблема нахождения математической модели, которое описывает зависимость управления от координат пространства состояния управляемой системы.

Постановка задачи. Рассматривается управляемая система [1]

(1)

где - фазовый вектор, – вектор управления, принимающий свои значения из области управления , являющаяся подмножеством .

Будем решать задачу оптимального управления (1), рассматривая всевозможные начальные состояния и каждый раз предписывая заранее известное конечное состояние управляемой системы. Тогда существует такая функция , заданная в фазовом пространстве и принимающая значения в области управления , что уравнение

(2)

определяет все оптимальные траектории. Значит, оптимальную управлению будем искать не в виде , а в виде . Следовательно, искомое оптимальное управление зависит от нахождения фазовой точки в фазовом пространстве в данный момент времени. Отсюда, если мы находимся в фазовой точке , то дальнейшее траектория должно быть оптимальным. Поэтому значение оптимального управления в момент прохождения фазовой точкой положения зависит только от самой , а не от того, в какой точке начиналась траектория и сколько времени фазовая точка двигалась.

Функция , определяющая уравнение оптимальных траекторий, называется синтезирующей функцией, а задачу нахождения синтезирующей функции называется задачей синтеза оптимального управления.

Пример. Рассмотрим задачу остановки маятника в положении равновесия, описываемого уравнением [2]

(3)

где -отклонение маятника от состояния равновесия, -сила, которая можно приложить к маятнику. Эта сила должно удовлетворять ограничению . Начальное положение маятника и начальная скорость заданы. Требуется за наменьшее время перевести маятник в состояние равновесия, т.е. на множество .

Делая замену переменных , , , , приведем эту задачу к задаче оптимального управления. Тогда поведение маятника описыавается уравнением

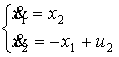(4)

Ограничение на управление имеет вид , , Требуется за наименьшее время остановить маятник в положении равновесия, т.е. перевести его в состояния в состояние покоя . При этом может оказаться, что начальное состояние заранее неизвестно. Например, маятник по действием каких-либо неизвестных сил переходит в состояние и нужно как можно скорее вернуть его в состояние покоя. Поэтому необходимо заранее решить задачу быстродействия для произвольного начального значения .

Пример. Рассмотрим задачу запуска ракеты с земли на космическую станцию [2]. Пусть ракета единичной массы движется прямолинейно в соответствии с законом движения

(5)

где -отклонение ракеты от какой-либо фиксированной точки, -ускорение ракеты, -сила, действующая на ракету в момент времени .

Предполагаем, что силу можно изменять со временем в пределах возможностей двигателя ракеты, которые определяются условием . В начальный момент времени ракета находится в состоянии . При этос можно придать ракете ограниченную начальную скорость . Требуется за наименьшее время перевести ракету в состояние , , т,е, с нулевой скоростью произвести стыковку с космической станцией, которая можеть подойти в любое из положений к заданному моменту времени.

Приведем данную задачу к задаче оптимального управления. Для этого введем новые переменные , , , . Таким образом, фазовый вектор объекта является двумерным , а уравнение движения имеет вид

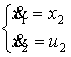(6)

Ограничение на управление задается множеством

.

Начальное множество имеет вид

,

а конечное множество имеет вид

.

Для решение приведенных задач нужно найти минимум скалярной функции, т.е. время перехода объекта из множества на множество . Аргументами этой функции являются не скалярные величины, а всевозможные допустимые управления . Необходимым условием оптимальности является принцип максимума Понтрягина.

Принцип максимума Понтрягина. Пусть на отрезке времени задано некоторое допустимое управление такое, что соответствующее решение переводит управляемой системы (1) из начального множества на конечное множество , т.е. удовлетворяет граничным условиям , . Тогда будем говорить, что пара , удовлетворяет принципу максимума Понтрягина на отрезке времени , если существует такое нетривиальное решение вспомагательной системы дифференциальных уравнений [3]

, (7)

что выполнены следующие три условия:

1) условие максимума

(8)

для всех ;

2) условие трансверсальности на множестве

; (9)

3) условие трансверсальности на множестве

. (10)

Здесь - знак скалярного произведения, с – константа.

Систему (7) называем сопряженной, а ее решение - сопряженной функцией. Это решение нетривиальна, если .

Решение сопряженной системы дифференциальных уравнений (7) существует на всем отрезке времени , единственное для любого начального значения и задается формулой Коши

(11)

Это решение нетривиально, если , поскольку матрица невырождена. Аналогично, если начальное значение для задано на правом конце отрезка времени , т.е. в точке , то решение системы дифференциальных уравнений (7) имеет вид

(12)

Также это решение будет нетривиальным, если , в силу невырожденности матрицы .

Литература:

1. Ибрагимов У.М. Об одном подходе решения задачи оптимального перехода // Вестник КазНУ им.Аль-Фараби, -Алматы, сер. мат. мех. инф. №4 (71), 2011. с.48-54.

2. Блогадатских В.И. Введение в оптимальное управление (линейное теория) –М:. Высш. шк., 2001. -239 с.

3. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. –М.: Наука, 1969. -384 с.