Математика / 1.Дифференциальные и интегральные уравнения

ФГУП «Сибирский научно- исследовательский институт авиации

им. С.А. Чаплыгина», Россия

Приближенно- аналитические соотношения динамики

продольного возмущенного движения автожира

К.т.н. Калмыков А.А.

Актуальность аналитического исследования динамики автожира обусловлена необходимостью предварительной оценки динамических характеристик автожира при проектировании [1], на которые существенное влияние оказывает непостоянство частоты вращения несущего винта (НВ).

При изменении параметров движения автожира (скорости полета V, угла атаки ротора a_р, и т.д.) с некотором фазовым отставанием из-за инерционности изменяется частота вращения авторотирующего НВ w, что, в свою очередь, приводит к изменению сил и моментов НВ, действующих на автожир.

В работе исследован переходный процесс после ступенчатой перекладки ротора на угол Dd_в в установившемся горизонтальном полете (ГП).

Решим линеаризованную систему уравнений возмущенного продольного движения, включающую дополнительное уравнение углового ускорения НВ, записанных в скоростной системе координат (СК), рисунок 1:

; (1)

; (2)

; (3)

; (4)

; (5)

где Х, Y – суммы проекций сил частей летательного аппарата (ЛА) на оси скоростной СК (индекс «а» опущен); Р – тяга двигателя; J – угол тангажа корпуса автожира; – угол наклона траектории; a_к – угол атаки корпуса; I_z – момент инерции автожира; I_р – момент инерции НВ относительно оси вращения; М_z – моменты тангажа, создаваемые частями ЛА; М_кр. – крутящий момент НВ; w_z = dJ / dt – угловая скорость тангажа. Значения сил отнесены к полетной массе автожира m₀. Индекс «р» («ротор») в обозначениях переменных относится к НВ, «к» – к корпусу автожира, «го» – к горизонтальному оперению; V₂ – скорость за винтом; Х_вр. – сопротивление корпуса. Индекс «0» означает, что значение переменной относится к исходному режиму полета.

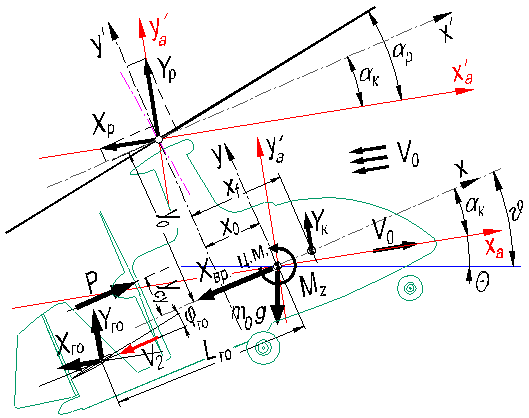
Рисунок 1 – Схема сил, действующих на автожир

Используя метод малых возмущений [2], линеаризуем систему (1)–(4) относительно исходного режима установившегося ГП:

d(DV)/dt = ×{[P^V cos a_к0 –(+)]DV– (P₀ sin a_к0 +)Da_к

+ (–)×–Dw – m₀ g Dq + F₁}, (6)

=[m₀ V₀]^-1×{(+++P^V sin a_к0)DV+(++

+Р₀ cos a_к0)Da_к +(++)×+Dw+ F₂}, (7)

= ×{DV +Da_к + ×+Dw + F₃}, (8)

= ×{DV+ Da_к + ×+Dw + F₄}; (9)

где F₁…F₄ – значения возмущающих сил и моментов

При рассмотренном ступенчатом отклонении НВ на угол Dd_в, приращение a_р вызовет соответствующее изменение линейных и угловых ускорений:

=(-/m₀)Dd_в; =(/[m₀V₀])Dd_в; =(/ I_z)Dd_в; =(/I_p)Dd_в.

Обозначим в (6) - (9) выражения перед DV, Da_к и т.д., отнесенные соответственно к m₀, m₀V₀, I_z и I_р, коэффициентами с_ik, где i – номер уравнения по порядку, k – обозначение переменной, при которой стоит коэффициент. Значения частных производных НВ могут быть найдены аналитически [3], получены с помощью численной имитационной модели (ИМ) динамики автожира [1, 4] или определены экспериментально.

Исключив q с помощью уравнения связи (5) и используя символ дифференцирования р, уравнения (6) - (9) принимают вид:

АU = –, где – вектор внешнего возмущения (управления):

(с1V –р)	(+ g)	(p –g)	с1w	´	DV	= –		. (10)
с2V	(р +)	(-1)р	с2w		Daк
с3V		(р –р^2)	с3w
с4V		р	(с4w– р)		Dw

Характеристическое уравнение запишется в виде:

a₅ р⁵ + а₄ р⁴ + а₃ р³ + а₂ р² + а₁ р + а₀ = 0; (11)

где a₅ = 1;

a₄ =- с_1V - - с_4w;

a₃ = с_1V с_4w - с_1V+ с_1V+с_4w- с_4w-+ с_2w - +- с_3w+ с_2V+ с_2V g - с_3V - с_1w с_4V;

a₂=с_1V с_4w-с_1V с_4w+с_1V-с_1V с_2w+с_1V-с_1V

+с_1V с_3w+с_4w +с_2w +с_3w- с_3w

- с_2w+с_4w -с_4w - с_3w- с_2Vс_4w

-с_2V с_4w g -с_2V-с_2Vg+с_1wс_2V+с_2V+ с_3V

- с_3V+ с_3V g- с_1w с_3V+с_3V с_4w -с_3V +с_1wс_4V

- с_1w с_4V - с_3w с_4V +с_2w с_4V +с_2w с_4V g;

a₁=с_2Vс_4w+с_2Vс_4w g+с_1w с_2V+с_2Vс_3w

-с_1w с_2V- с_2Vg -с_2Vс_4w -с_2Vс_3w-с_2Vс_3wg

- с_3Vс_4w + с_3Vс_4w – с_3Vgс_4w + с_3V gс_4w – с_2wс_3V

- с_1w с_3V+с_1wс_3V- с_1w с_3V- с_3Vс_4wg +с_3Vс_4w

+с_3Vg+с_2wс_3V+ с_2w с_3Vg +с_3w с_4V+с_3w с_4Vg

-с_3w с_4V – с_3w с_4V g + с_1wс_4V +с_2wс_4V + с_1wс_4V

- с_1wс_4V+с_3w с_4V g-с_3w с_4V -с_2wс_4V -с_2wс_4V g;

a₀= g (с_2V с_4w - с_2V с_3w +с_2w с_3V-с_3V с_4w -с_2wс_4V

+с_3w с_4V).

Первый вещественный корень характеристического уравнения (11) находится численно, после чего степень уравнения понижается до четвертой, решение которого известно.

Для оценки влияния непостоянства частоты вращения НВ на устойчивость движения, с помощью применения критерия Раусса- Гурвица [2, 5] к системе (10), определена область устойчивости автожира А-002 (линия 1, рисунок 2) в сравнении со случаем, не учитывающим изменение w (линия 2), в зависимости от центровки х₀ и скорости =V₀ /wR » m. Изменение частоты вращения НВ приводит к сохранению устойчивости движения до более задних центровок из-за затрат энергии ЛА на изменение w при возмущении.

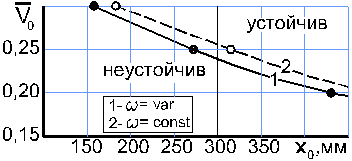
Рисунок 2 – Область устойчивости автожира

Приближенно- аналитическое решение переходного процесса при ступенчатой перекладке НВ на угол Dd_в= +1° в ГП на скорости m₀ = 0,3 сравнивается с численным (х₀ = 250 мм). В данном случае значения частных производных НВ и параметров исходного режима определены с помощью ИМ. Изменение a_р относительно угла атаки корпуса a_к учитывалось углом отставания Da_р(w_z) = - 8w_z / (g_лw₀), где g_л– массовая характеристика лопасти.

Характеристическое уравнение (11) имеет вещественный корень р₁ = n₀ < 0, определяющий сильнозатухающее апериодическое движение; и комплексно сопряженные корни р_2,3 = n₁ ± w₁i; р_4,5 = n₂ ± w₂i; соответственно характеризующие быстрозатухающее короткопериодическое движение автожира и слабозатухающее длиннопериодическое.

Общее решение уравнений (10) имеет вид:

DU = A_0u+A_1u×sin (w₁t + j_u1) +A_2u×sin (w₂t +j_u2) +DU_r, (12)

где UÎ {V, a_к, J, w}.

Частное решение системы (10) – приращения параметров движения DU_r после окончания переходного процесса, имеет вид:

DU = D_u /D(p); (13)

где D_u – определители, полученные из главного определителя D(р) (10) заменой соответствующих столбцов правыми частями уравнений. Положив в (10) р = 0, получим значения DU_r и передаточных функций (0):

DU_r= = (0) ×Dd_в;

DV_r=;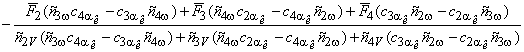

(0)=;

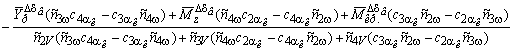Da_кr =;

Dw_r =;

DJ_r =/g +(с_1V /g)×DV_r + (+g)(Da_кr / g) +с_1w(Dw_r /g). (14)

Используя уравнение связи (5) к выражению (14), получим

Dq_r = [–+ с_1V ×(0) +×(0)+с_1w×(0)]×Dd_в /g =(0)×Dd_в.

Постоянные интегрирования найдем из начальных условий, для чего последовательно четырежды продифференцируем уравнения (12) для каждого параметра UÎ{V, a_к, J, w} при t = 0.

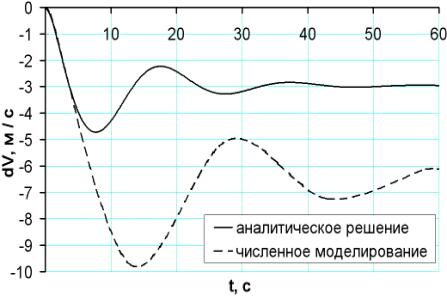
Полученный переходный процесс в сравнении с результатами моделирования приведен на рисунках 3, а–в; где нормальная перегрузка определена как n_y(t) = 1+×.

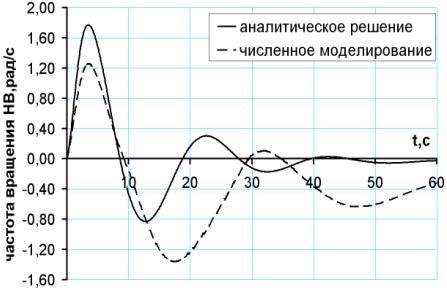
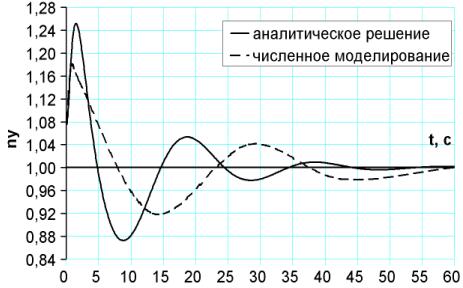
Аналитическое решение дает качественно правильное описание переходного процесса. Период колебательного движения автожира, определенный моделированием, превышает период, полученный аналитически, из-за значительной взаимосвязи продольного и бокового движений. Длиннопериодическое движение затухает слабо. Полученная аналитическим путем диаграмма n_y – n, качественно верно отражает ее характерные особенности [4].

Рисунок 3, а – Изменение скорости

Рисунок 3, б – Изменение перегрузки

Рисунок 3, в – Изменение частоты вращения НВ

Между аналитическим решением и численным имеются существенные количественные расхождения, обусловленные нелинейностью характеристик автожира, не учитываемых принятыми упрощающими допущениями.

Таким образом, исследования режимов, характеризующихся быстрым и значительным изменением параметров полета, целесообразно проводить с помощью математического моделирования, так как область применения аналитического решения весьма ограничена, а сложность сопоставима.

Выводы

1) Получены приближенно- аналитические соотношения возмущенного продольного движения автожира, учитывающие дополнительную степень свободы – непостоянство частоты вращения НВ

2) Исследованы динамическая устойчивость автожира и характер переходного процесса при ступенчатой перекладке НВ на малый угол. Выявлено, что изменение частоты вращения НВ повышает запас устойчивости автожира и оказывает существенное влияние на его динамику движения.

3) Показано, что исследования режимов неустановившегося движения автожира при больших изменениях полетных параметров, целесообразно проводить с помощью численного математического моделирования.

4) Получено значительное количественное расхождение между численным экспериментом и результатами расчета по аналитическим соотношениям. Очевидно, приращение изменение угла атаки НВ на 1 градус на скорости 200 км/ч некорректно считать малым. Получено качественное совпадение. Целесообразна проверка полученных результатов в летном эксперименте.

Литература

1. Калмыков А.А. Динамические модели автожира и нормирование условий нагружения конструкции: Автореферат диссертации канд. техн. наук – Казань, 2005 – С.16

2. Лысенко Н.М. Динамика полета. Устойчивость и управляемость ЛА. Вып. I. Издание ВВИА им. проф. Н. Е. Жуковского, 1966 – С.375

3. Есаулов С.Ю., Бахов О.П., Дмитриев И.С. Вертолет как объект управления. М.: Машиностроение, 1977 – С.192

4. Калмыков А.А. Реализуемые сочетания перегрузки и раскрутки НВ автожира // Известия ВУЗов. Авиационная техника, 2004, № 2. С.6-9

5. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. Изд-во второе. М.: «Наука», Главная редакция физико-математической литературы, 1972 – С. 767.