Математика/3
– Теория вероятности математическая статистика
К.т.н. Игнатьев В.М., Паненко Н.Н.
Южно-Российский
государственный политехнический университет, Россия
ПОСТРОЕНИЕ РЕГРЕССИОННЫХ УРАВНЕНИЙ ОБЕЗЗАРАЖИВАНИЯ ВОДЫ
ХЛОРСОДЕРЖАЩИМИ ПРЕПАРАТАМИ
Двухступенчатая схема очистки воды
обеспечивает осветление, обесцвечивание и обеззараживание воды, подаваемой для
хозяйственно-питьевых целей. Предусматривает следующие операции: коагулирование
воды, углевание, осветление ее в горизонтальных отстойниках и фильтрах с
применением флокулянтов, обеззараживание путем хлорирования [1]. Химические
методы обеззараживания природных и сточных вод предусматривают применение:
молекулярного хлора, гидрохлорида натрия и гидрохлорида кальция.
Обеззараживание воды называется процесс уничтожения находящихся там
микроорганизмов. В процессе первичной очистки вод задерживаются до 98 %
бактерий. Но среди оставшихся бактерий, а также среди вирусов могут находиться
патогенные (болезнетворные) микробы, для уничтожения которых нужна специальная
обработка воды – её обеззараживание.
В исследовании рассматривались
химические препараты: молекулярный хлор; гидрохлорид натрия, полученный
элетролизом; нейтральный гипохлорит кальция [2]. Опыты проводились при
температуре обеззараживаемой воды 20 °C. Исходное содержания клеток бактерий E-coli в 1 л воды составляло 1,2 млн кл./л. Доза препаратов
для обеззараживания содержала 1,5 мл/л активного хлора. Результирующим фактором
являлась доля погибших клеток (K) в зависимости от продолжительности
обеззараживания (t),
мин. Исследование зависимости доли погибших клеток при обеззараживании питьевой
воды хлорсодержащими препаратами позволило построить следующие регрессионные
модели.
Для
гидрохлорида натрия уравнения имеют следующий вид: функция Торнквиста 3-го типа
К = -0,00865 t 
(1) при коэффициенте корреляции r = 0,98978;
Парабола K = – 0,00008375 t2 +
0,017 t + 0,201 (2) при коэффициенте корреляции r = 0,98426.
Для
молекулярного хлора получены уравнения: функция Торнквиста 2-го типа К = 1,238
(3) при коэффициенте корреляции r = 0,99; парабола
K = – 0,00006551 t2 + 0,015 t + 0,177 (4) при
коэффициенте корреляции r = 0,9873.
Для
гидрохлорида кальция уравнения имеют следующий вид: Функция Торнквиста 2-го
типа К = 1,668
(5) при коэффициенте корреляции r = 0,99285 и
парабола K = – 0,0000303 t2 +
0,01 t + 0,019 (6) при
коэффициенте корреляции r = 0,99248.
Коэффициент корреляции процесса
обеззараживания уравнения (2) равен r = 0,98424 и
значим по критерию Стьюдента на 5 % уровне значимости, так как Тэкс = r∙
= 19,28., Tст (0,025; 12)
= 2,56 и Тэкс.> Tст. Значимость r указывает на наличие линейной связи данных опыта
времени экспозиции t и
значений, получаемых с помощью построенного уравнения (2). Так как значение критерия построенной модели превышает
значение теоретического критерия, то модель значима на 5 % уровне. Для всех
остальных регрессионных уравнений коэффициенты корреляции также значимы.
Расчёты по оценке значимости
уравнений (2),(3),(4),(5),(6) с помощью методов дисперсионного анализа [3]
сведены в табл. 1. Уравнение (1) не значимо по критерию Фишера, хотя имеет
значимый коэффициент корреляции.
Все построенные регрессионные
уравнения в табл. 1 значимы на 5 % уровне, но остатки (разница между значениями
опыта и модели) достигают 26,2 %. Поэтому для уравнений из табл. 1
требуется работа с остатками [3]. Сравнение зависимостей процесса обеззараживания
хлорсодержащими препаратами приведена на рис. 1. Кривая обеззараживания с
помощью гидрохлорида натрия K1 более результативна.
Таблица 1 – Дисперсионный
анализ для уравнений (2)÷(6)
|
Уравнение (2) |
|||||||
|
Источник |
Сумма квадратов |
Число степеней свободы |
Дисперсия |
||||
|
Регрессия |
0,764 |
2 |
3,82 |
||||
|
Остаток |
0,025 |
12 |
2,054·10-3 |
||||
|
Вариация |
0,789 |
14 |
- |
||||
|
Критерий уравнения |
Критерий теоретический |
||||||
|
3,82/0,002054=186,06 |
F(0,05;12;2) = 19,41 |
||||||
|
Уравнение (3) |
|||||||
|
Источник |
Сумма квадратов |
Число степеней свободы |
Дисперсия |
|
||||
|
Регрессия |
0,8399 |
2 |
0,42 |
|
||||
|
Остаток |
0,0005935 |
12 |
4,946·10-5 |
|
||||
|
Вариация |
0,84049 |
14 |
– |
|
||||
|
Критерий уравнения |
Критерий теоретический |
|
||||||
|
0,42/0,00004946=8491 |
F(0,05;12;2) = 19,41 |
|
||||||
|
Уравнение (4) |
|||||||
|
Источник |
Сумма квадратов |
Число степеней свободы |
Дисперсия |
|
||||
|
Регрессия |
0,819 |
2 |
0,41 |
|
||||
|
Остаток |
0,021 |
12 |
1,765·10-3 |
|
||||
|
Вариация |
0,84 |
14 |
– |
|
||||
|
Критерий уравнения |
Критерий теоретический |
|
||||||
|
0,41/0,001765=231,69 |
F(0,05;12;2) = 19,41 |
|
||||||
|
Уравнение (5) |
|||||||
|
Источник |
Сумма квадратов |
Число степеней свободы |
Дисперсия |
|
||||
|
Регрессия |
0,84623 |
2 |
0,42615 |
|
||||
|
Остаток |
0,00021 |
12 |
2,081·10-4 |
|
||||
|
Вариация |
0,84644 |
14 |
– |
|
||||
|
Критерий уравнения |
Критерий теоретический |
|
||||||
|
0,42615/0,0002081=24403 |
F(0,05;12;2) = 19,41 |
|
||||||
|
Уравнение (6) |
|||||||
|
Источник |
Сумма квадратов |
Число степеней свободы |
Дисперсия |
|
||||
|
Регрессия |
0,834 |
2 |
0,417 |
|
||||
|
Остаток |
0,012 |
12 |
1,051·10-3 |
|
||||
|
Вариация |
0,846 |
14 |
– |
|
||||
|
Критерий уравнения |
Критерий теоретический |
|
||||||
|
0,417/0,001051=394,26 |
F(0,05;12;2) = 19,41 |
|
||||||
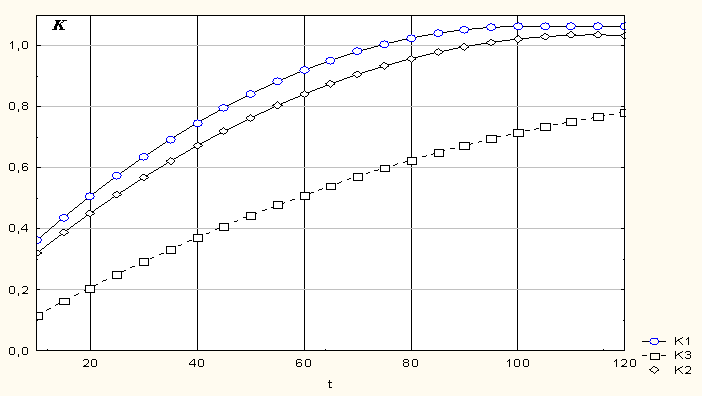Рисунок 1 – Зависимость
степени обеззараживания К от
продолжительности процесса t: Кривая К1 – гидрохлорид натрия; Кривая К2 –
молекулярный хлор; Кривая К3 – гидрохлорида кальция
ЛИТЕРАТУРА:
1.
Кедров
В.С. и др. Водоснабжение и водоотведение: Учебник. – М.: Стройиздат, 2002. –
336 с.
2.
Дрововозова
Т.И. Основы энергосберегающей технологии фотохимического обеззараживания воды и
напитков на её основе. Монография / Т.И. Дрововозова, В.М. Игнатьев, В.В. Гутенёв, В.В. Денисов. – Новочеркасск:
НГМА, 2006. – 196 с.
3.
.Дрейпер
Н.Р., Смит Г. Прикладной регрессионный анализ. – М.: Диалектика, 2007. –
912 с.
Хочу послать на конференцию Научная индустрия (Чехия)
до 25 надо оплатить.
1 стр 120 рублей.
1 сборник 120 рублей.
Наташа! Сможете оплатить? Корректируйте.