Сланбекова
А.Е., Фазылова Л.С.
Карагандинский
государственный университет им. Е.А. Букетова, Казахстан
Применение системы MATLAB при решении задач на условный
экстремум функции многих переменных
Постановка задачи. Будем рассматривать задачу
,
где 
- выпуклое замкнутое
множество пространства 
- пространства
векторов длины n, а функция 
- выпуклая дифференцируемая функция на 
и 
Пусть 
- некоторое начальное
приближение к точке минимума 
функции 
. По методу проекции градиента последовательность приближений 
к точке 
строится по
следующему правилу [1]:
, (1)
где 
- положительная
величина, а 
- проекция точки 
на множество 
.
Величина 
из (1) в различных
вариантах метода проекции градиента вычисляется по-разному. Укажем способ,
который применялся в данной работе. Выбирают
какую-либо постоянную 
и в методе (1) на
каждой итерации полагают 
, а затем проверяют условие монотонного убывания функции
. (2)
И, при необходимости, дробят величину 
, добиваясь выполнения условия (2).
Условием окончания вычислений
по методу проекции градиента является выполнение неравенства 
где 
- заданная точность.
Далее представлена
численная реализация метода проекции градиента в системе MATLAB 7 на примере двумерной выпуклой квадратичной функции.
При решении задачи применялись графические возможности системы MATLAB 7 [2].
Пример.
Решить задачу выпуклого
программирования
, 
методом проекции градиента,
завершая вычисления при выполнении неравенства 
.
Решение. 1) Приведем графический
способ решения задачи. Построим графики функций 
, 
. Для этого в системе MATLAB введем следующие процедуры:
>>
[X,Y]=meshgrid(-3:0.1:3);
>>
Z=1/2*X.^2+1/6*Y.^2; surf(X,Y,Z)
>>
[X,Y]=meshgrid(-3:0.1:3);
>> Z=X+Y-1;
>> hold on
>> mesh(X,Y,Z)
>> hidden off
Результат представлен
на рисунках 1, 2.
2) Построим в системе MATLAB итерационный процесс (1) для данной задачи.
Сначала для наглядности выполним один шаг итерации метода проекции градиента. В
качестве начального приближения выберем, например, точку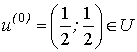 
. Затем вычислим градиент функции 
:
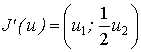. Применим формулу (1) для вычисления первого приближения к
точке минимума 
функции 
:
, где 
, а параметр метода 
выбираем из условия (2): 
. Например, 
.
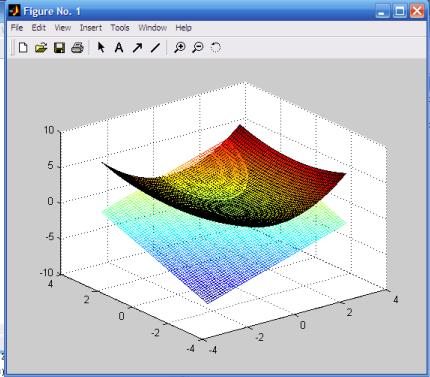
Рисунок 1
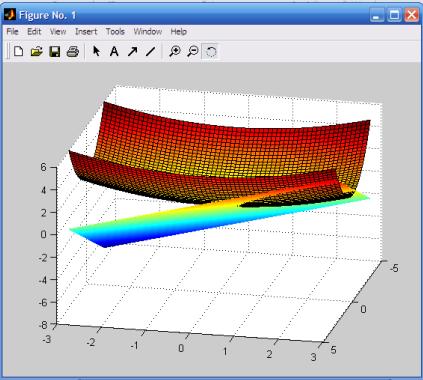
Рисунок 2
1 шаг. Так как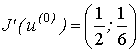 
и 
, то по формуле (1) при 
получим
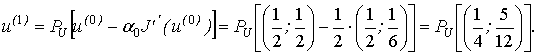
Полученная точка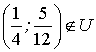 
, так как не выполняется условие 
, т.е. 
. Поэтому найдем проекцию полученной точки на множество 
: 
.
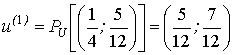Заданная точность не
достигнута: 
.
Результаты вычислений на
следующих шагах метода проекции градиента приведены в следующей таблице:
|
k |
|
|
|
|
|
0 |
(0,5000;
0,5000) |
|
(0,5000; 0,3333) |
(0,2500; 0,5833) |
|
1 |
(0,4167; 0,5833) |
0,1179 |
(0,4167; 0,1944) |
(0,2083; 0,4861) |
|
2 |
(0,3611; 0,8889) |
0,0786 |
(0,3217; 0,1533) |
(0,1633; 0,3415) |
|
3 |
(0,3299; 0,8232) |
0,0517 |
(0,2333; 0,0476) |
(0,1465; 0,1415) |
|
4 |
(0,2798; 0,7879) |
0,0313 |
(0,1233; 0,0136) |
(0,4998; 0,0339) |
|
5 |
(0,2566; 0,7633) |
0,0117 |
(0,0733; 0,0036) |
(0,2198; 0,6339) |
|
6 |
(0,2477; 0,7478) |
0,0023 |
Точность достигнута |
|
Окончательно имеем
, 
.
Литература:
1. Васильев
Ф.П. Численные методы решения экстремальных задач. М.: Наука, 1981. - 400 с.
2. Кетков
Ю.Л., Кетков А.Ю., Шульц М.М. MATLAB 7: программирование, численные методы.
СПб.: БХВ-Петербург, 2005. - 752 c.