Автор: Ічанська Надія Григорівна,

учениця 10-М класу Полтавська гімназія № 6, Україна

Науковий керівник: Подошвелев Юрій Георгійович,

к.ф.-м.н, доцент кафедри математич-ного аналізу та інформатики Полтав-ського національного педагогічного університету імені В.Г. Короленка, Україна

Усенко Інна Леонідівна, учитель математики вищої кваліфікаційної категорії, учитель-методист, Україна

Використання симетрії при розв’язуванні рівнянь і нерівностей

На сучасному етапі розвитку науки і техніки роль математики особливо зростає, бо практично жодна наука не обходиться без її застосування[1]. Одним із центральних її аспектів є математичне моделювання, що широко використовується в дослідженні систем різної природи, але особливого значення воно набуває в соціальному управлінні, в рамках методології системного підходу. Найефективнішими моделями вважаються аналітичні, підґрунтям яких є математична фізика, а точніше диференціальні рівняння в частинних похідних[2].

Якщо дослідник ставить за мету навчитеся ефективно досліджувати вказані моделі, то він стикається з проблемою пошуку точних розв’язків рівнянь математичної фізики. Метод симетрійної редукції Софуса Лі покликаний вирішити проблематику цього питання.

Отже, досліднику край необхідно знайомство з симетрійними методами досліджень. У зв’язку з широкою сферою застосування симетрійних методів, серед різноманіття математичних тем на початковому етапі ознайомлення було обрано тему «Застосування симетрії при розв’язанні рівнянь та їх систем»[3].

Одним із підходів розв’язування зворотних рівнянь вищих порядків є використання симетричних многочленів.

Многочлен вигляду, де називають зворотнім, якщо в ньому коефіцієнти, що рівновіддалені від кінців співпадають, тобто

Рівняння ліва частина якого є зворотній многочлен називається зворотнім рівнянням.

Теорема: Будь-який зворотній многочлен парного степеня можна представити в вигляді де та – деякий многочлен степеня від . Будь-який зворотній многочлен непарного степеня зводиться до зворотного многочлена парного степеня шляхом ділення даного многочлена на . (Теорема наводиться без доведення).

Із теореми випливає, що для розв’язання зворотного рівняння парного степеня, потрібно ввести заміну і використати наведені нижче вирази:

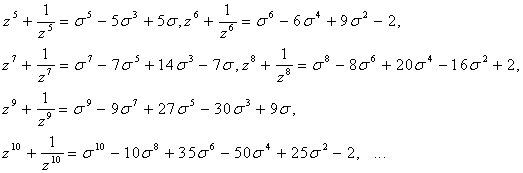
Приклад. Розв’язати рівняння

Розв’язання. Задане рівняння є зворотнім рівняння непарного 11 степеня. Згідно теореми розділимо його ліву частину на :

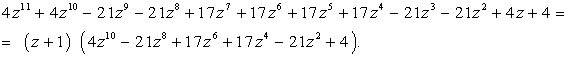
Таким чином, ми отримали два рівняння

та

Коренем першого рівняння є .

Друге з отриманих рівнянь є зворотнім рівнянням 10 степеня. Спростивши ліву частину якого, отримаємо:

Оскільки не є коренем заданого рівняння, то отримаємо:

Винесемо за дужки:

.

Добуток дорівнює нулю лише тоді, коли

або

Друге з отриманих рівнянь є біквадратним, тому для його розв’язання введемо заміну: Після введення заміни, отримаємо квадратне рівняння .

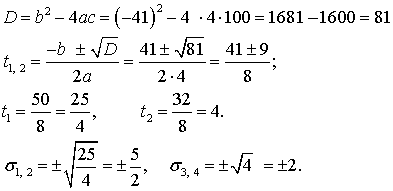
Таким чином, отримано п’ять коренів:

А значить і п’ять рівнянь:

.

Розв’язавши, та врахувавши корінь, одержимо одинадцять коренів заданого рівняння:

Обрана тема є первинною ланкою ознайомлення з аналітичними аспектами теорії симетрії. Другим етапом планується застосування симетрійних перетворень до кривих другого порядку, адже виходячи з методу аналогій, вони уподібнюються лінійним диференціальним рівнянням в частинних похідних другого порядку[4,5].

Із даного етапу дослідження, результати можна використовувати при підготовці учнів до олімпіадних задач та при проведенні факультативних занять із математики[6,7,].

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Болтянский В.Г., Виленкин Н.Я. Симметрия в алгебре. — М.: Наука, гл. ред. физ.-мат. лит., 1967.

2. Мордкович А.Г. Алгебра для начала математического анализа. 11 класс. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А.Г. Мордкович, П.В. Семенов.-4-е изд., стер.-М.:Мнемозина, 2010.-287с.:ил.

3. Винберг Э.Б. Симметрия многочленов. М.:МЦНМО, 2001.-24с,:ил.

4. Александрова Н.В. Математические термины. Справочник.- М.: Наука, 1978.

5. Многочлены: Учебное пособие/ Ларин С.В.- Красноярск: КГПУ, 2007г.

6. Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре М.: «Просвещение», 2002.

7. Збірник задач з математики для вступників до вузу / В.К. Єгерев, В.В. Зайцев, Б.А. Кордемський та ін.; За ред. М.Л. Сканаві / Пер. з рос.: Є.В. Бондарчук, Ю.Ю. Костриця, Л.П. Оніщенко. – К.: Вища школа, 1992.