Математика/5. Математическое моделирование

К.т.н. Демиденко Л.Л., Коринченко Г.М.

Магнитогорский государственный технический университет, Россия

Использование метода покоординатного расщепления для решения трехмерной задачи затвердевания непрерывнолитого слитка

Задача определения динамики затвердевания расплава во времени может быть решена с помощью средств математического моделирования.

Математическое моделирование является удобным инструментом для исследования процесса затвердевания непрерывнолитого слитка, прогнозирования движения фронта кристаллизации во времени и пространстве с учетом выделения скрытой теплоты кристаллизации, роста кристаллов в двухфазной зоне; поиска оптимальных условий охлаждения и определения основных теплотехнических, технологических параметров и т.д.

Решение математической модели для двумерного пространственного распределения было рассмотрено в [1,4,5].

Применение третьей пространственной координаты позволяет исследовать кинетику объемной кристаллизации при гетерогенном зарождении кристаллов, динамику нарастания твердой корочки, рассчитать термические напряжения в твердой фазе с учетом эффекта наращивания, химическую неоднородность сплава и т.п.

Для расчета температурного поля непрерывнолитого слитка необходимо решить неоднородное уравнение теплопроводности:

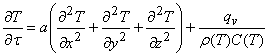, (1)

где ─ изменение нестационарного температурного поля,

─ время, c;

─ коэффициент температуропроводности, м²/c;

─ плотность внутренних источников теплоты, Вт/м²;

─ удельная теплоемкость, кДж/(кг К);

─ плотность, кг/м³.

Величина плотности внутреннего источника теплоты определяется как:

,

где ─ скрытая теплота кристаллизации, кДж/кг;

─ скорость затвердевания сплава.

Начальные условия состоят в задании для некоторого начального момента времени распределения температур

Граничные условия отображают реальные условия теплового взаимодействия между окружающей средой и поверхностью слитка для каждой зоны.

В [2,3] для упрощения решения задачи затвердевания выделение теплоты кристаллизации учитывают при помощи введения эффективной теплоемкости , которая является физической характеристикой затвердевания слитка. Зададим величину эффективной теплоемкости в виде системы:

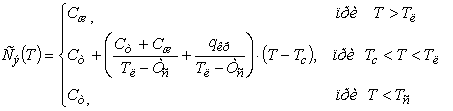
Аналогично представим плотность металла как функцию от температуры:

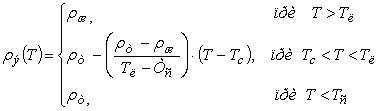
Коэффициент эффективной теплопроводности с учетом соотношения фаз рассчитывается:

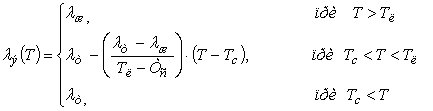
Таким образом, неоднородное уравнение теплопроводности (1) сводится к однородному уравнению:

(2)

В результате математического моделирования определяется пространственное изменение температурного поля во времени в зависимости от интенсивности охлаждения и закономерности его изменения при варьировании внешних параметров.

Выбор вычислительного алгоритма, с помощью которого можно получить при моделировании решение конкретной задачи, является важным. Перепишем уравнение (2) в виде:

. (3)

Для решения такого класса задач наиболее эффективными являются конечноразностные методы. Их построение основывается на идее построения приближенных сеточных решений: спроектировать данное уравнение на сетку, заменяя входящие в него функции сеточными, а частные производные – их простейшими разностными аппроксимациями.

При дискретизации многомерных задач целесообразно использовать экономичные локально-одномерные схемы: их построение основано на введении на каждом шаге по времени промежуточных этапов, на каждом из которых записывается одномерная аппроксимация по одному из пространственных направлений. Многомерная задача «расщепляется» на последовательность одномерных задач по каждой из координат. Поэтому такие схемы называются схемами расщепления по координатам. В подобных схемах отсутствует аппроксимация на каждом промежуточном этапе, т.е. ни одна из одномерных разностных схем по отдельности не аппроксимируют исходное уравнение, но в совокупности они обеспечивают эту аппроксимацию. Погрешности аппроксимации промежуточных слоев при суммировании уничтожаются.

Схема покоординатного расщепления для трехмерного уравнения теплопроводности (3) представлена в виде:

,

,

.

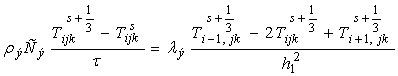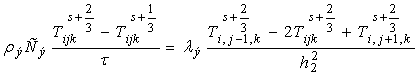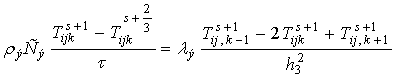Каждое из этих разностных уравнений представляет собой неявную схему для одномерного уравнения теплопроводности. Получающиеся системы уравнений имеют трехдиагональные матрицы с явным диагональным преобладанием и решаются методом прогонки. Такая схема безусловно устойчива и не требует больших вычислительных затрат. Решение системы уравнений представляет собой значения функции, найденной в узлах сетки, иначе, каркас решения данной задачи.

Литература:

1. Демиденко Л.Л. Математическое моделирование охлаждения непрерывнолитого слитка в МНЛЗ. Монография. ─ Магнитогорск: ГОУ ВПО «МГТУ», 2007. ─ 108с.

2. Емельянов В.А. Тепловая работа машин непрерывного литья заготовок. ─ М.: Металлургия, 1988. – 143 с.

3. Самойлович Ю.А. Микрокомпьютер в решении задач кристаллизации слитка. ─ М.: Металлургия, 1988. – 182 с.

4. Демиденко Л.Л. Математическое моделирование как инструмент прогнозирования рациональных режимов МНЛЗ. //Математика. приложение математики в экономических, технических и педагогических исследованиях. Сборник научн. тр. / Под ред. М.В. Бушмановой. Вып. 3. ─ Магнитогорск: МГТУ, 2005. 273 с. С.141-144.

5. Демиденко Л.Л., Коринченко Г.М., Черняев А.А. Численное решение уравнения теплопроводности методом покоординатного расщепления. // Математика. Приложение математики в экономических, технических и педагогических исследованиях: Сборник научн. тр. / Под ред. М.В. Бушмановой. Вып. 4. ─ Магнитогорск: ГОУ ВПО «МГТУ», 2006. С.18-20.

6. Демиденко Л.Л., Коринченко Г.М. Разработка трехмерной модели температурного поля непрерывнолитого слитка. //Математика. Приложение математики в экономических, технических и педагогических исследованиях: Сборник научн. тр. / Под ред. М.В. Бушмановой. Вып. 4. ─ Магнитогорск: ГОУ ВПО «МГТУ», 2006. С.119-121.