Математика / 5. Математическое моделирование

Калмыков А.А., к.т.н., Барсук В.Е., к.т.н., Морозов М.В.

ФГУП «Сибирский научно- исследовательский институт авиации

им. С.А. Чаплыгина»

Компьютерный пилотажный стенд

управляемого пространственного движения автожира

Использование опережающего моделирования полета значительно повышает безопасность проведения летных испытаний (ЛИ) и результативность испытательных полетов, еще на этапе проектирования позволяет выявить особенности динамики, определить нагрузки на неустановившихся режимах полета, достаточность выбранного диапазона управления и других конструктивных и компоновочных решений. Так, Руководство по летной эксплуатации опытного автожира А-002 было разработано задолго до первого полета по результатам моделирования на имитационной модели (ИМ), тем не менее, в дальнейшем оно подвергалось непринципиальным уточнениям.

В практике имитационного моделирования полета используются модели различных типов. Большинство задач решается в рамках модели, в которой полет ЛА описывается как движение твердого тела без учета эффектов аэродинамической нестационарности [4, 5].

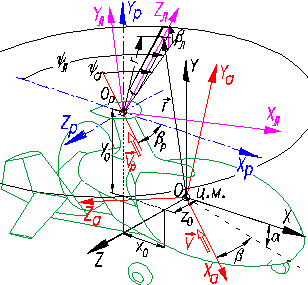
При описании движения используются стандартная связанная система координат (СК) ОXYZ и дополнительные СК, связанные с осями частей ЛА, в частности, вращающаяся СК лопасти ОлXлYлZл (рисунок 1). Автожир в полете рассматривается как твердое тело, имеющее 7 степеней свободы, включая вращательную степень свободы несущего винта (НВ).

Рисунок 1 – Основные СК автожира

В математической модели применяется подход, при котором корпус рассматривается как твердое тело, а карданный НВ заменяется его равнодействующей, рассматриваемой как одна из внешних сил, действующих на корпус (при других схемах втулок необходимо еще учитывать моменты, передаваемые с НВ на корпус). При наличии компенсации взмаха параметры НВ пересчитываются в плоскость эквивалентного винта [6]. При работе компенсатора лопасти изменяют угол установки j в зависимости от угла взмаха b_л:

j = j₀ - k b_л, где k – коэффициент компенсации.

НВ, у которого шаг лопастей изменяется циклически по первой гармонике:

j = j₀ – cos y_л – sin y_л, где = – k a₁; = – k b₁ [6, с. 129];

при аэродинамическом расчете может рассматриваться как винт с постоянным шагом j₀, но с другим (эквивалентным) углом атаки [6, с.109]:

a_э = a_р – = a_р + k b₁,

l_э = l – m = l + k b₁ m;

где a₁, b₁ – амплитуды 1 гармоники махового движения;

, – углы отклонения автомата перекоса (АП) в каналах тангажа и крена соответственно;

a_р – угол атаки НВ;

m = cos a_р – коэффициент режима работы винта;

= ; V_р – воздушная скорость у ротора;

l = sin a_р – v_{i ср} / w R – коэффициент протекания;

v_{i ср} – средняя индуктивная скорость;

w – угловая скорость вращения НВ;

R – радиус НВ.

Компоненты сил задаются в осях, связанных с плоскостью, относительно которой угол установки лопасти остается постоянным, то есть плоскостью эквивалентного НВ.

Влияние махового движения на динамику автожира учитывается углами дополнительного отклонения конуса лопастей НВ Da₁, Db₁ при криволинейном движении. Таким образом, движение корпуса автожира описывается шестью стандартными уравнениями пространственного движения в проекциях на оси связанной СК [5, 7]:

, (1)

= М; (2)

и дополнительным уравнением углового ускорения НВ:

dw / dt = SM_кр / I_р, (3)

где F – главный вектор действующих сил; – вектор кинетического момента; М – результирующий вектор внешних моментов; SM_кр= M_кр.а +M_кр.г - M_тр.– крутящий момент НВ; M_кр.а – аэродинамический крутящий момент; I_p – осевой момент инерции НВ; M_тр.– момент трения; M_кр.г = – I_p × w (w_x × b₁ – w_z× a₁) – дополнительный крутящий момент инерционной природы; w_x,z – угловые скорости автожира.

ИМ представляет собой программу, численно интегрирующую уравнения (1) – (3) пространственного движения автожира. Программа выдает текущие значения параметров полета и позволяет изменять положение органов управления, что дает возможность интерактивно «пилотировать» ИМ автожира. Математическая модель автожира включает в себя математические модели его частей и систем управления. В основной процедуре на каждом шаге интегрирования по времени определяются силы и моменты частей автожира и выполняется интегрирование уравнений движения. Полученные значения параметров полета {V}, {w}, Н, X_g, Z_g, J, g, y, w [8] и их производные являются исходными данными для следующего шага. Цикл интегрирования выполняется непрерывно до тех пор, пока не произойдет вмешательство в управление. В этом случае выполнение программы переходит в цикл опроса управления, где орган управления получает соответствующее дискретное приращение своего положения (рисунок 2). Тяга НВ Т_р и крутящий момент M_кр.а рассчитывается непосредственным интегрированием по сечениям лопасти в итерационном цикле расчета v_{i ср} на каждом шаге Dt интегрирования по времени (рисунок 3).

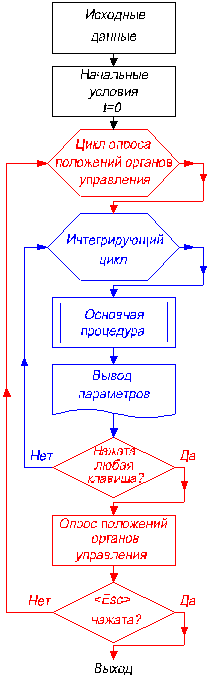
Рисунок 2 – Блок-схема ИМ

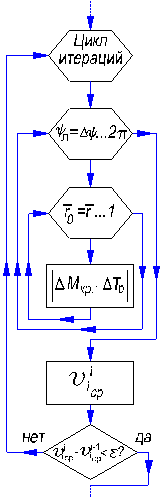
Рисунок 3 – Итерационный цикл vi ср – Тр

Текущие значения температуры Т, влажности Х, давления р и плотности r изменяются от высоты H в соответствии с Международной стандартной атмосферой (МСА) или задаются отклонениями от стандартных значений. Кроме того, используются служебные команды управления программой: изменение шага интегрирования, запись в файл, изменение дискретности записи в файл, «пауза», включение демпферов крена и тангажа, автоматики прыжкового взлета и пр.

Расчет производится для N азимутов, полученные значения усредняются за оборот. Преимуществами этого типа модели является ее большая адекватность, так как тяга НВ определяется по фактическим углам атаки сечений лопасти. Недостаток – увеличение вычислительных затрат. Для решения задач, не связанных с достижением больших углов атаки НВ и угловых скоростей, может быть использована более простая модель, в которой силы НВ рассчитываются через коэффициенты этих сил по линейной теории.

Значения аэродинамических коэффициентов сопротивления C_хr и подъемной силы C_yr в сечении лопасти задаются функциями местных угла атаки a_r и числа М_r по данным круговой обдувки профиля [9] в рамках гипотезы стационарности. Как указывается в [10, с.14], [11], для относительно малооборотных НВ влияние нестационарности на аэродинамические характеристики невелико.

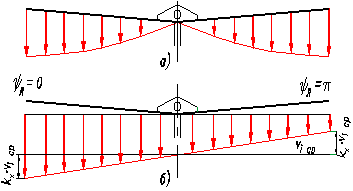
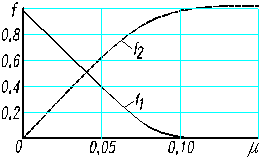
Нелинейная модель авторотирующего НВ учитывает неравномерность поля индуктивных скоростей, задаваемых в виде воронкообразного распределения и скосов. Вклад каждого закона задается коэффициентами f₁ и f₂, так зависящих от m, что на осевых режимах остается только осесимметричное распределение (f₁ = 1), а на больших скоростях – только скосы (рисунок 4). Коэффициенты f₁ и f₂ (рисунок 5) определяются экспериментально [7].

Рисунок 4 – Распределение vi по диску НВ

Рисунок 5 – Коэффициенты f1 и f2

Выражение для местной индуктивной скорости v_i имеет вид

v_i (,y_а) = v_{i ср}×[× f₁ (m) + (1 + {k_x × cos y_а + k_z × sin y_а }× ) ×f₂ (m)], (4)

где k_x и k_z – градиенты продольного и поперечного скосов; y_а = y_л – b_p – угол «воздушного» азимута лопасти (рисунок 1), y_л – угол азимутального положения лопасти, отсчитываемый от конструктивной оси автожира, b_p – угол скольжения ротора; = r / R – относительный радиус сечения лопасти.

Продольный перекос влияет также на величину завала конуса вбок, который увеличивается на угол, численно равный приращению относительной индуктивной скорости на конце лопасти в переднем и заднем положениях [6, с.108]. Добавка к b_1э из-за неравномерности индуктивных скоростей находится по выражению:

Db₁ = f₂× k_x× v_{i ср} / wR.

Изменение индуктивной скорости при криволинейном движении учитывается поправками p_x l₁ и p_z l₁:

р_z,х · l₁ = (3S_гш / 2r S_ом R²) × (k_л /m)× w_z,x / w, (5)

где

S_гш– статический момент лопасти относительно оси горизонтального шарнира (ГШ); r – плотность воздуха; S_ом – ометаемая площадь НВ; k_л – число лопастей.

Выражения (5) дают правильный результат, когда коэффициент протекания l мал по сравнению с m (при m > 0,15). При m < 0,15 значение A рассчитывается как для m = 0,15.

Моделирование зоны концевых потерь осуществляется уменьшением C_yr на конце лопасти по эллиптическому закону [12]:

C_уr = C_уr(a_r, M)×; C_xr = C_xr(a_r, M);

где В – коэффициент концевых потерь, рассчитываемый по выражению, предложенному Прандтлем и Бентцем [10, с.98]. Для учета влияния земли используется формула Чизмена и Беннета [13, с.152]:

t =,

где Z – расстояние от ВПП до ротора;

t₀ – коэффициент тяги НВ, определяемый без учета влияния земли.

Применимость модели НВ ограничена значением m_max = 0,5.

В модели приближенно учитывается обдув НВ струей маршевого винта. Скорость за винтом принимается равной скорости V₂, определяемой по теории идеального винта. Обдуваемая область определяется пересечением конуса НВ со струей, имеющей цилиндрическую форму. Известны конструктивные решения, применявшиеся на автожирах [14, с.17], использования потока от маршевого винта для раскрутки НВ перед разбегом. Принимается, что окружная скорость в струе пропорциональна w_су r_су [15, 16]. При обдувке не учитывается изменение махового движения из-за относительной малости обдуваемой площади, значение v_{i ср} определяется изменением тяги ротора Т_р. При обдуве диска НВ из-за увеличения его сопротивления имеются потери КПД СУ [16, с.91]. В первом приближении тяга Р уменьшается на величину возрастания сопротивления НВ. При выполнении условий попадания сечения лопасти в область пространства, занимаемого струей СУ [1], компоненты скоростей в сечениях лопасти рассчитываются по отдельному алгоритму [1].

Управляющие параметры модели: положения ручки управления (РУ) циклическим шагом НВ по крену и тангажу, общего шага (ОШ) лопастей j₀₇, руля направления (РН), рычагов управления двигателем (РУД) a_руд и шагом маршевого винта a_рушв; угол установки стабилизатора j_го; усилие на рычаге включения системы раскрутки НВ Р_фрикц., разовые команды тормоза шасси и НВ.

При пересчете тяги Р силовой установки (СУ) учитывается влияние атмосферных условий (Т, р, Х) и Н на мощность двигателя N_i [16].

Значения тяги и потребляемой винтом мощности от положения a_руд и a_рушв и скорости набегающего на диск потока, определяется по результатам расчетов коэффициентов (l_с), (l_с) в сечениях лопасти маршевого винта с учетом поправок на сжимаемость, затенение винта и потерь на обдув оперения, и уточняются по результатам эксперимента.

Приближенно [16], [17] учитываются силы Y_су(a_су), Z_су(b_су), возникающие в плоскости диска при его косой обдувке.

Приемистость СУ моделируется ограничением скорости изменения частоты вращения коленвала двигателя n_су. При быстрых перемещениях РУД приращение частоты вращения на оставшуюся разницу Dn_су происходит с запаздыванием по времени Dn_су / на следующих шагах интегрирования Dt после окончания перемещения РУД.

Киль и стабилизатор выделяются в качестве отдельных элементов планера для адекватного учета угловых скоростей автожира, влияния НВ и СУ, в струе которой находится часть размаха консолей оперения. Силы в сечениях поверхностей оперения рассчитываются по данным круговой обдувки.

Значения аэродинамических производных корпуса и сопротивление эквивалентной «вредной пластинки» åС_хS получены расчетным путем [18, 19, 20]. Подъемная и боковая силы определялись в линейной постановке до углов атаки и скольжения 40°, далее интерполировались уменьшением до 0 при углах 90°. В отсутствии данных продувок такое допущение обосновано тем, что на пилотаже на больших скоростях углы атаки корпуса не превышают 25…40°, а на малых, например, режимах парашютирующего спуска или прыжкового взлета, где могут достигаться большие углы атаки, малы силы корпуса. Подобное допущение используется и при моделировании динамики движения вертолета [7, с.104]. Аэродинамические силы корпуса приложены в ц.д., массовые силы – в ц.м. автожира.

Коэффициент трения качения колеса включает коэффициент лобовой силы при раскрутке колеса с учетом проскальзывания [21, с.304]:

f_тр.кач. = f_тр.ст.(V_к, p_пн.) + f_х(),

где p_пн..– давление зарядки пневматика; V_к – скорость колеса с учетом проскальзывания.

Коэффициент трения скольжения при включенных тормозах основных колес принимается равным меньшей из величин: коэффициенту f_{тр. ск.} или усилию страгивания с тормоза. Коэффициент трения скольжения колеса вбок принимается равным f_{тр. ск.}.

Крутящий момент, передаваемый трансмиссией М_спр, ограничивается несущей способностью фрикционной муфты [М_фрикц.] = М_фрикц.(Р_фрикц., Dn_фрикц.), зависящей от усилия прижима дисков Р_фрикц. и окружной скорости взаимного проскальзывания дисков со стороны двигателя и ротора Dn_фрикц.= j₁ n_су – j₂ n, где j₁ и j₂ – передаточные отношения от двигателя к муфте и от муфты к НВ соответственно. Управление муфтой в ИМ осуществляется изменением усилия прижима дисков, выраженного через усилие на рычаге включения Р

Масса автожира пересчитывается из текущего остатка топлива m_топл.= m_топл.0 –.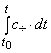

Сходимость численного решения исследовалась для случая наибольших достигаемых ускорений автожира при маневре варьированием шага Dt.

Моделированием были выявлены особенности динамики, подтвержденные впоследствии в испытаниях: тенденция к кабрированию и потере скорости после отрыва; перебалансировка автожира и изменение w при криволинейном движении; тенденция к переходу в набор высоты при выходе из виража, «клевок» при вводе в пикирование из-за запаздывания снижения частоты вращения НВ [3], [22]- [25].

Для увеличения w на разбеге [3], [24], [25], ротор отклоняется назад на большой угол управления d_в, часть диска попадает в струю маршевого винта, что уменьшает «просадку» оборотов НВ в начале движения.

Выявлены особенности, связанные с «перекачкой» энергии между автожиром и ротором. Практическое применение, нашла, в частности методика поэтапной «накачки» скорости - оборотов НВ n при взлете с малой тяговооруженностью [3]. Суть методики заключается в ступенчатом наборе скорости и раскрутке НВ на разбеге. Из-за инерционности ротора частота вращения НВ не успевает заметно уменьшиться при даче РУ «от себя» для увеличения скорости. Взлет выполняется при достижении необходимого сочетания n – V.

Численное моделирование позволяет определить параметры режимов, критичных для прочности. К таковым относятся, прежде всего, режимы, приводящие к возрастанию изгибающих моментов на карданной втулке [1], [2]:

- режимы с увеличением перегрузки и раскруткой НВ (горка, вираж);

- с увеличением n_y и уменьшением n (подрыв шага, прыжковый взлет [23], [27]);

- взлет с разбегом с недораскрученным ротором и высокой скоростью в момент отрыва.

На рисунке 6 приведен пример выполнения полета на ИМ (по данным опытного А-002). Летчики – испытатели СибНИА В.Е. Барсук и И.А. Мосейкин отмечают высокую степень соответствия имитационного моделирования фактическим особенностям пилотирования автожиров А-002 и А-002М.

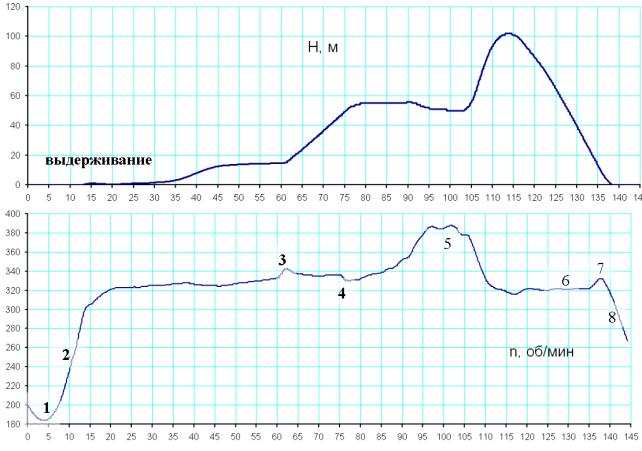
1- провал оборотов НВ в начале разбега, 2- раскрутка при разбеге, 3- раскрутка при взятии РУ «на себя» при переходе в набор высоты; 4- просадка оборотов НВ при даче РУ от себя при переводе в ГП после окончания набора, 5- раскрутка НВ в вираже, 6- уменьшение оборотов на снижении (из-за уменьшения земной перегрузки при большом наклоне траектории), 7- раскрутка при взятии РУ на себя на выравнивании, 8- уменьшение оборотов на пробеге

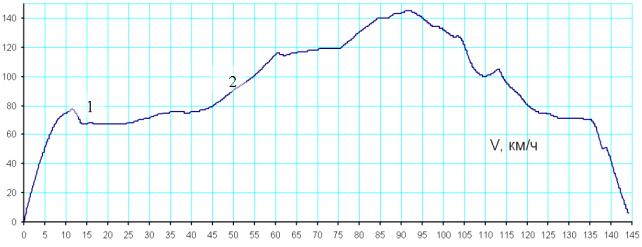
1 - потеря скорости после отрыва, 2 - разгон скорости при выдерживании в горизонте

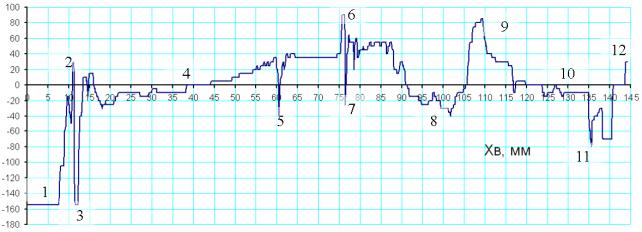
1- удержание РУ полностью «на себя» для наиболее эффективной раскрутки НВ, 2- отдача РУ от себя для парирования нарастающего кабрирования, 3- парирующее (останавливающее) движение для прекращения поворота на пикирование, 4- постепенное смещение РУ вперед для увеличения скорости, 5-взятие РУ на себя для перевода в набор высоты, 6- перевод в ГП (прямое движение), 7- останавливающее движение, 8- взятие РУ на себя для поддержания требуемой перегрузки в вираже, 9-дача РУ от себя при выводе из виража, 10- взятие РУ для уменьшения скорости на предпосадочном снижении, 11- выравнивание, 12- дача РУ от себя на пробеге для опускания носовой стойки

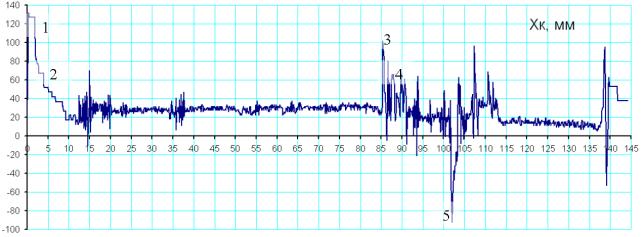
1- удержание РУ влево на разбеге для выравнивания реакций колес, 2- постепенное возвращение РУ ближе к нейтрали в канале крена по мере раскрутки НВ и увеличения эффективности управления, 3- дача РУ влево для ввода в вираж, 4- возвращение к нейтрали при достижении требуемого крена, 5- отклонение РУ вправо для вывода из виража. Заметны сильная поперечная перебалансировка при резких дачах РУ в канале тангажа (15, 35 и 140 секунды).

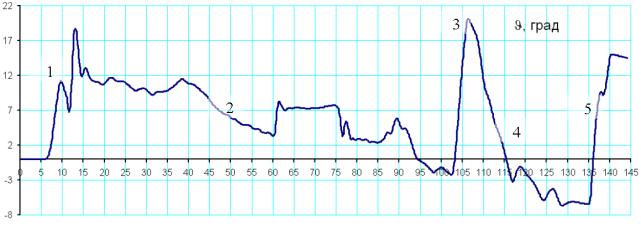
1- увеличение угла тангажа после отрыва от ВПП, 2- уменьшение тангажа при переводе в горизонтальный полет, 3- возрастание тангажа при выходе из виража (из-за раскрутки ротора в вираже), 4- уменьшение тангажа при переводе в снижение, 5-увеличение угла тангажа на выравнивании.

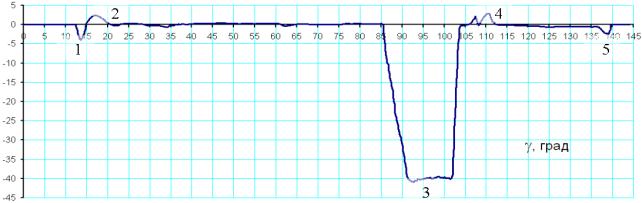
1- тенденция к кренению вправо после отрыва; 2, 4, 5– поперечная перебалансировка при резких дачах РУ, 3- левый крен в вираже

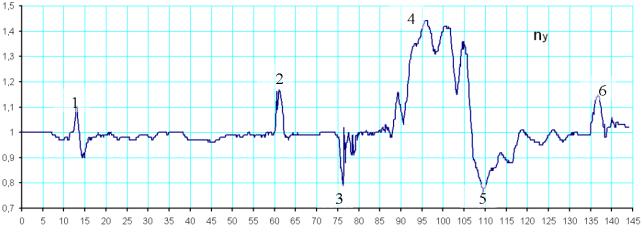
1- заброс перегрузки после отрыва, 2- перевод в набор высоты, 3- дача РУ от себя при переводе в ГП, 4- поддержание требуемой n_y в вираже, 5- вывод из виража, 6- выравнивание

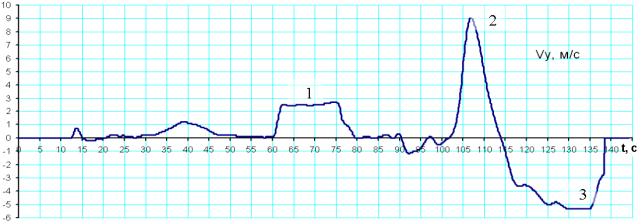
1- участок установившегося набора, 2- набор после выхода из виража, 3- уменьшение вертикальной скорости при выравнивании.

Рисунок 6 – Пример моделирования полета

На рисунках обозначены следующие параметры:

Х_в, Х_к – положение ручки управления (РУ) в каналах тангажа и крена;

J, g – углы тангажа и крена;

n_y – нормальная перегрузка;

V_y – вертикальная скорость.

Выводы

1. Разработана математическая модель пространственного управляемого движения автожира, используемая как инструмент исследования динамики автожира.

2. Определен потребный шаг интегрирования, обеспечивающий сходимость численного интегрирования дифференциальных уравнений пространственного движения автожира при выполнении энергичных маневров с быстроменяющимися параметрами [1].

3. Выявлены основные особенности динамики автожира, получено распределение характеристик авторотации по диску на неустановившихся и критических режимах [28].

4. Отработаны теоретически на ИМ, и впоследствии подтверждены в летных испытаниях А-002 методики пилотирования автожира на разбеге и при взлете по- самолетному [3].

5. Получена приближенная количественная оценка влияния эффекта обдува части диска НВ струей маршевого винта и ее направления вращения.

Литература

1. Калмыков А.А. Динамические модели автожира и нормирование условий нагружения конструкции: Автореферат диссертации канд. техн. наук – Казань, 2005 – С.16

2. Калмыков А.А. Реализуемые сочетания перегрузки и раскрутки несущего винта автожира // Известия ВУЗов. Авиационная техника, 2004, № 2. С.6-9

3. Калмыков А.А., Филиппов А.Н. Анализ летных характеристик автожира // Труды всероссийской научно- технической конференции, Новосибирск, ФГУП «СибНИА им. С.А. Чаплыгина», 15-17 июня 2004. С.162-170

4. Красовский А.А. Основы теории авиационных тренажеров. М.: Машиностроение, 1995 – С.304

5. Есаулов С.Ю., Бахов О.П., Дмитриев И.С.. Вертолет как объект управления. М.: Машиностроение, 1977 – С.192

6. Миль М.Л., А.В. Некрасов и др. Вертолеты. Расчет и проектирование, Т.1. Аэродинамика. М.: Машиностроение, 1966 – С.455.

7. Браверман А.С., Вайнтруб А.П. Динамика вертолета. Предельные режимы полета. М.: Машиностроение, 1988 – С.280.

8. Микеладзе В.Г., Титов В.М. Основные геометрические и аэродинамические характеристики самолетов и ракет. М.: Машиностроение, 1990 – С.144

9. Радченко П.И. Круговая обдувка профиля NACA 23012 в аэродинамической трубе Т-103Н ЦАГИ // Труды ЦАГИ. Вып.161. М.: Издательский отдел ЦАГИ, 1959 – С.23.

10. Пейн П.Р. Динамика и аэродинамика вертолета. М.: Оборонгиз, 1963 – С.492

11. Проскуряков А.П.. Влияние нестационарности потока на аэродинамические характеристики лопасти автожира // Труды ЦАГИ, 1939. № 460

12. Полынцев О.Е. Динамика и прочность авторотирующего несущего винта: Автореферат диссертации канд. техн. наук – Казань, 2003 – С.16

13. Джонсон У. Теория вертолета. Т1., Т2. М.: Мир, 1983 – С. 1017

14. Братухин И. П. Автожиры. Теория и расчет. ОНТИ НКТП СССР, 1934 – С.111.

15. Колесников Г.А., Марков В.К., Михайлюк А.А. и др. Аэродинамика летательных аппаратов. М.: Машиностроение, 1993 – С.544

16. Кравец А.С. Характеристики воздушных винтов. М.: Государственное издательство оборонной промышленности, 1941 – С.259.

17. Бюшгенс Г.С., Студнев Р.В. Аэродинамика самолета. Динамика продольного и бокового движения. М.: Машиностроение, 1979 – С. 349

18. Ранцан Я.Я. Определение нестационарных аэроупругих характеристик самолета при воздействии подвижных порывов // Научно-методические материалы по аэроупругости ЛА – ВВИА им. Н.Е. Жуковского, 1983

19. Калинин А.И. Суммарные и распределенные аэродинамические характеристики изолированных поверхностей при малых дозвуковых скоростях. Труды ЦАГИ, вып.1503. М.: Издательский отдел ЦАГИ, 1973

20. Петров К.П. Аэродинамика элементов ЛА. М.: Машиностроение, 1985 – С.272

21. Морозов В.И., Пономарев А.Т., Рысев О.В. Математическое моделирование сложных аэроупругих систем. М.: «Физико- математическая литература», 1995 – С.736

22. Калмыков А.А. Особенности взлетных режимов автожира, имеющего заднее положение центра масс // Сборник трудов Х Всероссийского научно- технического семинара по управлению и навигации ЛА (26-27 июня 2001). Самара, 2002. С.279-284

23. Калмыков А.А., Полынцев О.Е. Бутырин С.А. Моделирование «прыжкового» взлета автожира// Труды 12-й Байкальской международной конференции. Секция «Управление летательными аппаратами и их системами» Иркутск, 2001. С.43-48

24. Калмыков А.А., Полынцев О.Е., Сомов Е.И. Имитационное моделирование петли Нестерова на автожире // Актуальные проблемы авиационных и аэрокосмических систем, 2002, №1 (13). С.56-66

25. Калмыков А.А., Полынцев О.Е., Сомов Е.И., Ранцан Я.Я. Особенности динамики взлетных режимов автожира // Труды 12-й Байкальской международной конференции. Секция «Управление летательными аппаратами и их системами» Иркутск, 2001. С. 58-65

26. Миль М.Л. О разбеге автожира // Техника Воздушного Флота, 1934, №5 – С.23

27. Миль М.Л. Автожир, взлетающий без разбега // Техника Воздушного Флота, 1935. №8

28. Полынцев О.Е., Калмыков А.А., Ранцан Я.Я. Распределение аэродинамических характеристик по диску авторотирующего несущего винта// Труды 12-й Байкальской международной конференции. Секция «Управление ЛА и их системами». Иркутск, 2001. С.123-127.