Физика/1.Теоретическая физика
Д.т.н. Розов А. Л.
Санкт-Петербургский
Государственный Политехнический Университет, Россия
Уравнения электродинамики
Максвелла для медленно движущихся сред
В
настоящее время принято считать, что теория Максвелла в рамках классической
механики позволяет получать уравнения электродинамики только для неподвижных сред. Для описания электромагнитных
явлений в движущейся среде применяются уравнения Минковского, представляющие
собой уравнения Максвелла для неподвижных сред, записанные с использованием
принципа относительности (аналогичные
уравнения получаются из электронной теории Лоренца) (см., например, [1,2]).
Электромагнитные явления на практике, как правило,
используются в условиях медленно движущихся сред (скорости значительно меньше
релятивистских) и находятся в условиях применимости классической механики.
Возникает задача описания этих явлений методами электродинамики Максвелла.
Основу теории Максвелла составляют два закона,
полученные экспериментально как для
неподвижных, так и подвижных сред (см., например, [3]):
- закон индукции Фарадея
![]()
![]() ;
(1) - закон Ампера
;
(1) - закон Ампера
![]() , (2)
, (2)
где ![]() и
и ![]() векторы электрического и магнитного
напряжения, магнитной индукции и плотности тока, соответственно;
векторы электрического и магнитного
напряжения, магнитной индукции и плотности тока, соответственно; ![]() и
и ![]() нормальные компоненты векторов
нормальные компоненты векторов ![]() и
и ![]() к произвольной поверхности
к произвольной поверхности ![]() , ограниченной
замкнутым контуром
, ограниченной
замкнутым контуром ![]() и
и ![]() время.
время.
Интегрируя обе части (1) в
лабораторной системе координат, относительно которой рассматривается движение,
и применяя теорему Стокса, получаем
![]() ,
(3)
,
(3)
где ![]() вектор скорости контура.
вектор скорости контура.
Уравнение (3) описывает все
случаи электромагнитной индукции, открытые Фарадеем.
Вводя векторный ![]() и скалярный
и скалярный ![]() потенциалы, находим из (3)
потенциалы, находим из (3)
![]() . (4)
. (4)
Запишем (4) в виде
![]() ,
(5)
,
(5)
где ![]() напряжение электрического поля,
индуцированного изменением во времени магнитного поля
напряжение электрического поля,
индуцированного изменением во времени магнитного поля
![]() ,
(6)
,
(6)
и ![]() напряжение электрического поля,
индуцированного движением контура
напряжение электрического поля,
индуцированного движением контура
![]() .
(7)
.
(7)
Фарадей, исследуя феномен
индукции, использовал проводники. Как показали эксперименты Вильсона [4], в
случае диэлектриков напряжение электрического поля, индуцированного движением
контура, равно ![]() , где
, где
![]() ,
(8)
,
(8)
![]() диэлектрическая константа.
диэлектрическая константа.
Таким образом, для общего случая
проводников и диэлектриков (5) записывается в виде
![]() .
(9)
.
(9)
Дифференциальная форма (9),
являющаяся обобщением (3), имеет вид
![]() . (10)
. (10)
Уравнение (10) описывает все
известные случаи электромагнитной индукции.
Интегрируя (2) и учитывая
различные виды токов [4-7], получаем
![]() , (11)
, (11)
где ![]() ,
, ![]() и
и ![]() вектора электрической индукции, плотности
тока проводимости и плотности свободно движущихся зарядов, соответственно.
вектора электрической индукции, плотности
тока проводимости и плотности свободно движущихся зарядов, соответственно.
Последние два члена правой
части (11), отсутствовавшие у Максвелла, учитывают токи, исследованные Роуландом
и Рентгеном и Эйхенвальдом.
В рамках теории Максвелла к
уравнениям (10-11) следует добавить
![]() , (12)
, (12)
а также уравнения состояния
(материальные уравнения), которые для тел с линейными параметрами имеют вид [8]
![]() , (13)
, (13)
где ![]() электрическая константа,
электрическая константа, ![]() и σ абсолютная проницаемость и
проводимость тела, соответственно.
и σ абсолютная проницаемость и
проводимость тела, соответственно.
Уравнения (10-13) составляют
уравнения Максвелла электродинамики медленно движущихся сред. Имеется 17
уравнений для 16 неизвестных. Таким образом, одно из уравнений является дополнительным
ограничивающим условием.
Сравнение теории с известными экспериментальными
данными
Рассмотрим скорость
электромагнитных плоских волн в медленно движущейся немагнитной среде.
Уравнения Максвелла для
медленно движущейся среды (10-13) в отсутствие свободных зарядов и токов
принимают вид
![]()
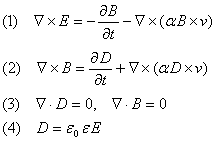 . (14)
. (14)
Так как нас интересуют только
члены, линейные относительно скорости, то для плоских волн можно положить
![]() ,
(15)
,
(15)
где ![]() скорость света в неподвижном теле,
скорость света в неподвижном теле, ![]() показатель преломления тела.
показатель преломления тела.
С учётом (14)(3) имеем
![]() . (16)
. (16)
Подставляя (15) и (16) в
(14)(1)-(14)(2) и используя (14)(4), получаем
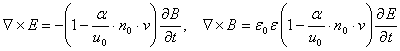 . (17)
. (17)
Вычисляя ротор первого
уравнения (17) и используя второе уравнение (17), приходим к уравнению
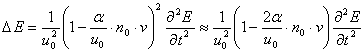 . (18)
. (18)
Это волновое уравнение
соответствует скорости распространения
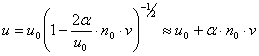 , (19)
, (19)
согласующейся
с известными экспериментальными данными [5,6,9].
Сравнение
уравнений Максвелла и Минковского
Формально различие между
предложенными уравнениями Максвелла и уравнениями Минковского состоит в форме представления закона
индукции. В уравнениях Максвелла этот закон представлен уравнением (3) (для проводников), а в
уравнениях Минковского (в приближении первого порядка скорости) – уравнениями
(20) - (21) [3,7,10]
![]() ,
(20)
,
(20)
![]() ,
(21)
,
(21)
где ![]() и
и ![]() векторы напряжения электрического поля в
стационарной и движущейся средах, соответственно;
векторы напряжения электрического поля в
стационарной и движущейся средах, соответственно; ![]() и
и ![]() те же, что и в уравнениях (1) и (3).
те же, что и в уравнениях (1) и (3).
Уравнение (20) является
общепринятой дифференциальной формой закона индукции Фарадея. Но это уравнение
неполное, так как не описывает индукцию вследствие движения (открытую Фарадеем).
Подстановка уравнения (21) в остальные уравнения Минковского преобразует
производные от ![]() в производные от
в производные от ![]() . В результате уравнение
(20) трансформируется в уравнение (3), но в остальных уравнениях Минковского образовавшиеся
производные от
. В результате уравнение
(20) трансформируется в уравнение (3), но в остальных уравнениях Минковского образовавшиеся
производные от ![]() имеют нефизичную
природу и могут вызвать погрешности при проведении расчётов электромагнитного
поля.
имеют нефизичную
природу и могут вызвать погрешности при проведении расчётов электромагнитного
поля.
Заключение
Выведены уравнения электродинамики медленно движущихся сред на основе
теории Максвелла в рамках классической механики, согласующиеся с известными
экспериментальными данными. Проведено
сравнение полученных уравнений Максвелла и используемых в настоящее время уравнений Минковского. Показано, что различие
заключается в форме представления закона индукции. Обосновано преимущество предложенных
уравнений.
Литература
[1]
Болотовский Б. М., Столяров С. Н. // Современное состояние электродинамики
движущихся сред. Успехи физических наук. 1974. Т. 114. Вып. 4. С. 569.
[2]
MacCall M., Censor M. // Am. J. Phys. 2007. Vol. 75. № 12. P. 1134.
[3] Sommerfeld A. Electrodynamik Leipzig: Akademische
Verlagsgesellchaft, 1961. P.12, 264.
[4] Wilson H. A. // Philos. Trans. R. Soc. London, 1904. Ser. A 204. P. 121.
[5] Becker R.
Electronentheorie. Leipzig, 1933. Sections 45, 46.
[6] Panofsky W. and Phillips M. Classical
Electricity and Magnetism. Cambridge-Mass.: Addison-Wesley, 1955. P. 117, 174.
[7] Pauli W. Theory of relativity. London:
Pergamon, 1958. P.111, 99.
[8] Maxwell J. C. A Treatise on Electricity and Magnetism. New York: Dover, 1954. Section
619.
[9]
Tonnelat M.-A. The Principles of Electromagnetic
Theory and of Relativity. Dordrecht-Holland: Reidel, 1966. P.115.
[10]
Тамм И. Е. Основы теории электричества. М.: “ Наука“, 1976. C. 532.