ИССЛЕДОВАНИЕ ИЗОТЕРМ СОРБЦИИ ВОДОРОДА

В СИСТЕМЕ МАГНИЕВЫХ ИНТЕРМЕТАЛЛИДОВ

Большое внимание, которое уделяется в последнее время синтезу новых перспективных гидридных интерметаллических материалов, объясняется их нетоксичностью, доступностью и относительной дешевизной. Такие интерметаллиды очень привлекательны как для накопления и хранения водорода, так и для практического использования в качестве электродов батарей электропитания [1]. Водородосорбционная емкость кристаллов Mg₃MnNi₂, Mg₃TiNi₂, Mg₃AlNi₂, LaMgNi₄, CeMgCo₄ и других, способных поглощать водород, составляет 5,4-7,6 вес. % водорода. [7,8].

Исследование кинетики водородной абсорбции – десорбции в соединении CeMgCo₄ показало, что в системе CeMgCo₄– Н₂ наблюдается образование двух гидридов (дейтеридов): с относительно малым количеством водорода формируется более устойчивая α фаза CeMgCo₄Н₄, а при большей концентрации водорода в системе образуется β фаза CeMgCo₄Н₆. При этом в процессе абсорбции кристаллическая решетка расширяется так, что увеличение ее объема составляет 20%. Экспериментальные изотермы абсорбции – десорбции демонстрируют гистерезисный эффект (рис.1) [1]. Изгибы на кривых гистерезисной петли указывают на реализацию фазового перехода α → β.

Настоящая работа посвящена построению статистической теории процессов абсорбции – десорбции водорода в системе CeMgCo₄ – Н₂, выяснению условий термодинамического равновесия формирующихся фаз и построению изотермы этого процесса. Интерес также представляет выяснение возможности проявления сорбционного гистерезисного эффекта и влияния на него фазового перехода α → β.

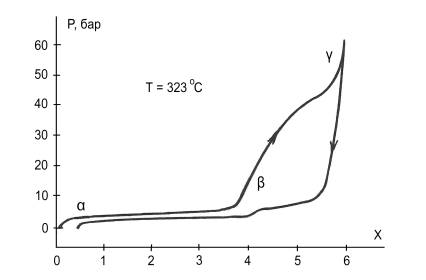
Рис. 1. Экспериментальные изотермы абсорбции

– десорбции системы CeMgCo₄ – Н₂[1]

С этой целью был проведен расчет свободных энергий F_i гидридных фаз α = CeMgCo₄Н₄, β = CeMgCo₄Н₆ с использованием известной формулы [2-6]

, (1)

где і = α, β; E_i– внутренняя конфигурационная энергия i-й фазы, определяемая суммой энергий межатомных взаимодействий, W_i – термодинамическая вероятность распределения атомов кристалла по их позициям, рассчитываемая по правилам комбинаторики, N_H – количество водородных атомов в кристалле, λi – их активность, k – постоянная Больцмана, Т – абсолютная температура.

Для решения поставленной задачи использовались упрощающие предположения: кристаллическая решетка принималась геометрически идеальной, межатомные взаимодействия учитывались только для ближайших атомных пар, корреляция в замещении позиций решетки атомами не учитывалась, зависимость энергий межатомных взаимодействий от концентрации водорода принималась квадратичной, использовалась известная формула зависимости активности атомарного водорода в кристалле от внешнего давления

λ_i = G_ip^1/2, (2)

где р – давление; G_i = const для каждой фазы.

При расчете внутренней конфигурационной энергии Е_i слагаемые с энергиями взаимодействия пар металлов вносятся в постоянное слагаемое Е_оi этой энергии. Энергия Е_i определяется по формуле

где N_CH, N_MH, N_KH, N_HH – числа ближайших атомных пар CeH, MgH, CoH, HH, а u_CH, u_MH, u_KH, u_HH – энергии их взаимодействия. Числа ближайших пар N_CH, N_MH, N_KH, N_HH находим, учитывая геометрию кристаллической решетки.

Обозначим через 6N число позиций атомов металлов Ce, Mg, Co. Тогда количество атомов Ce, Mg, Co определяется соответственно числами N, N, 4N. Числа позиций атомов водорода в α и β фазах соответственно равны 4N и 6N. Некоторые из этих позиций вакантны.

Пусть с и c_ν – концентрации атомов водорода и вакантных позиций. Для α фази CeMgCo₄Н_Х (0 ≤ x ≤ 4) эти значения равны

с = N_H/ 4N = x / 4, c_ν = 1 - c. (3)

С учетом принятых упрощений находим свободную энергию α фазы

, (4)

где обозначено U_α = U'_αc + U"_αc², U'_α= , U"_α= 6u_HH. Энергии U'_α,U"_α зависят от концентрации водорода, что обусловлено значительным расширением кристаллической решетки в процессе абсорбции.

Полученная формула (4) определяет зависимость свободной энергии α фазы от температуры, давления (с учетом (2)), концентрации атомов водорода, их активности (коэффициента G_α) и энергетических параметров взаимодействия атомных пар.

Равновесная концентрация водорода находится из условия минимума свободной энергии . С учетом (4) и квадратичной зависимости энергий U'_α,U"_α от концентрации водорода получим

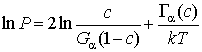, (5)

где Г_α(с) = γ_ос³ + γ'с² + γ"с + γ^*, а константы γ_о, γ', γ", γ^* определяются через энергии u_CH, u_MH, u_KH, u_HH.

По формуле (5) были рассчитаны изотермы водородной абсорбции – десорбции в кристалле CeMgCo₄Н_Х, определяющие зависимость величины Р от концентрации водорода для разных температур с использованием экспериментальных данных процесса гидрирования – дегидрирования этого кристалла при температуре 323˚С согласно рис.1. Оценка показала, что G_α = 1 и энергетические параметры соответственно равны γ_о = 4,16 эВ, γ' = - 6,24 эВ, γ" = 2,08 эВ, γ* = 0,01 эВ. На рис.2 представлены изотермы водородной сорбции кристалла CeMgCo₄Н_Х.

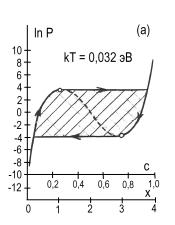
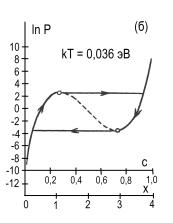
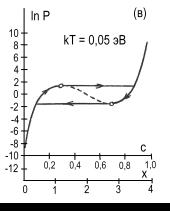
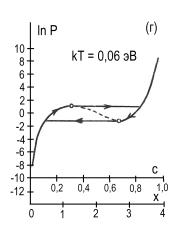
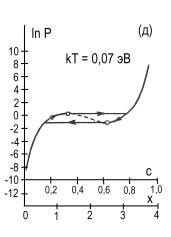
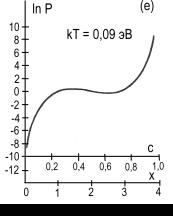
Рис. 2. Расчетные изотермы абсорбции – десорбции водорода в магниевом интерметаллиде CeMgCo₄Н₄, построенные по формуле (5) для различных температур, равных kT=0,032; 0,036; 0,050; 0,060; 0,070; 0,090 эВ (кривые а,б,в,г,д,е). Пунктирные участки кривых соответствуют нестабильному состоянию системы. Кружочками на кривых отмечены экстремальные точки. Заштрихованная область кривой 2а характеризует сорбционный гистерезисный эффект. Координаты с, х определяют содержание водорода в интерметаллиде: 0 ≤ с ≤ 1, 0 ≤ х ≤ 4.

На графике видно проявление сорбционного гистерезисного эффекта. При этом гистерезисная петля с ростом температуры сужается, укорачивается и исчезает.

Таким образом, разработанная статистическая теория водородной абсорбции – десорбции в кристалле CeMgCo₄ с образованием гидридов (дейтеридов): α фазы CeMgCo₄Н₄ и β фазы CeMgCo₄Н₆ – позволила изучить водородную сорбционность кристаллов для разных температур, объяснить и обосновать закономерности изотерм этого процесса, наблюдающиеся экспериментально. Установлена возможность появления гистерезисного эффекта, который исчезает с повышением температуры.

Выполненный расчет показывает, что экспериментальное исследование изотерм водородной сорбции в кристаллах может позволить по их виду выявить наличие или отсутствие в системе фазовых превращений, а также определить возможную температуру фазового перехода при его наличии.

Литература

1. Денис Р.В. Структура и водородосорбционные свойства новых соединений и сплавов на основе магния / Р.В.Денис, В.В.Березовец, И.В.Ковальчук и др. // Водородное материаловедение и химия углеродных наноматериалов. – К., 2009. – С. 40-43.

2. Матысина З.А. Атомный порядок и свойства сплавов.– Д., 1981.– 112 с.

3. Матысина З.А. Водород и твердофазные превращения в металлах, сплавах и фуллеритах / З.А.Матысина, Д.В.Щур. – Д., 2002. – 420 с.

4. Матисина З.А. Растворимость примесей в металлах, сплавах, интерметаллидах, фуллеритах / З.А.Матысина, С.Ю.Загинайченко, Д.В.Щур. – Д., 2006. – 514 с.

5. Смирнов А.А. Молекулярно-кинетическая теория металлов. – М., 1966. – 488 с.

6. Смирнов А.А. Теория сплавов внедрения – М., 1979. – 368 с.

7. Denys R. V. New Mg–M–Ni (M = Mn, Ti, Al) alloys as efficient hydrogen storage materials / R. V. Denys, I. Yu. Zavaliy et al. // Hydrogen materials science and chemistry of carbon nanomaterials. – 2007. – P. 332-335.

8. Chotard J. N. Hydrogen induced site depopulation in the LaMgNi₄ hydrogen system / J. N. Chotard, D. Sheptyakov, K. Yvon // Z. Kristallogr. – 2008. – V. 223. – P.690-696.