Д.т.н. Филонин О.В., аспирант Талызин Ю.Б., студент Николаев П.Н.

Самарский государственный аэрокосмический университет

имени академика С.П. Королёва, Россия

Математическое моделирование поведения

интеллектуальных группировок миниспутников на

планетарных орбитах, решающее задачи томографической реконструкции параметров атмосфер

251654656 Одним из наиболее перспективных направлений детального исследования планетарных атмосфер является метод, основанный на решении обратных задач радоновского типа, с помощью радио и лазерного зондирования атмосферного слоя. Наиболее перспективным, на наш взгляд, для этой цели является способ предложенный авторами [1]. Суть его заключается в том, что с помощью основного средства доставки (ОСД) на орбиту данной планеты транспортируется семейство малых спутников с массами порядка 10 кг. Каждый такой спутник, содержит: миниатюрный гироскоп, многопроцессорный блок для текущих вычислений орбитальных данных и параметров реконструкций, модуль связи, лазерный дальномер, устройство для импульсного лазерного зондирования атмосферного слоя, приёмо-передающий СВЧ-блок для радиозондирования, ионные или плазменные микродвигатели ориентации (ДО) и другие модули, в зависимости от особенностей конкретных решаемых задач. Как правило, ОСД располагается на стационарной орбите, поэтому группы малых исследовательских спутников, размещаемых на заданной орбите, целесообразно размещать на промежуточных средствах доставки (ПСД). ПСД стартуют с ОСД на заданную орбиту, и с них производится запуск малых спутников на исследовательскую орбиту, с учётом геометрии их распределения см. рис. 1.

Для решения поставленных задач – реконструкция пространственного распределения параметров атмосферы планеты, с помощью методов основанных на обращении Радона, прежде всего, необходимо точно знать конфигурацию орбиты движения каждого спутника и точные значения расстояний между ними. Действительно, даже в простейшем случае, в предположении круговой орбиты и строго распределённых на равных расстояниях совокупности спутников (рис. 1) получение хордовых данных, например, для задачи радиотомографии ионной компоненты атмосферы задача достаточно сложная. В этом случае зону реконструкции кольцевую зону при двумерной реконструкции целесообразно разбить на пересекающиеся круговые зоны восстановления см. рис. 1. Траектория зондирующего сигнала, таким образом, оказывается распределенной в нескольких зонах восстановления, при этом геометрия зондирования напоминает геометрию веерного пучка. Следовательно, возникает задача по разделению хордовых данных для данной круговой зоны восстановления, с другой стороны необходимо в каждой такой зоне свести хордовые данные к ортогональной геометрии проецирования и далее доопределить недостающие данные до заданного формата реконструкции.

Движение искусственного спутника планеты в первом приближении можно рассматривать как движение материальной точки бесконечно малой массы в поле тяготения центрального тела массой M под действием сил, определенных потенциальной функцией U, и совокупности сил, не имеющих потенциала. В этом случае дифференциальные уравнения движения частицы в инерциальной прямоугольной системе координат, связанной с центральным телом M, можно представить в виде:

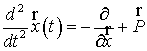, (1)

н.у. , где . Отметим, что первое слагаемое в U — потенциал, обусловленный притяжением сферической планеты, рассматриваемой как материальная точка, а второе слагаемое представляет собой потенциал возмущающих сил; вектор положения спутника; t - физическое время; r - модуль вектора положения;, - универсальная гравитационная постоянная; - градиент.

В качестве возмущающей силы, например для Земли, имеющей потенциал в задачах динамики ИСЗ, рассматривается, как правило, влияние несферической составляющей гравитационного поля Земли [2]. Все же остальные силы, включая влияние Луны и Солнца, положение которых задается либо таблично, либо в виде рядов, полученных вне задачи о движении ИСЗ, относятся к силам, не имеющим потенциала.

Отметим, что при введении в уравнения (1) силы, обусловленной влиянием несферичности Земли, следует помнить, что уравнения движения записаны в инерциальной системе координат, а потенциал гравитационного поля Земли отнесен к вращающейся системе координат, жестко связанной с Землей. Преобразования, связывающие эти системы координат, описаны в [3].

В действительности, реальные орбиты спутников, далеки от круговых. Это объясняется неравномерностью распределения массы планеты относительно её геометрического центра. Поэтому в теории движения искусственных спутников приято считать, что спутник – материальная точка движется в потенциальном поле планеты, функция потенциала - потенциал притяжения или силовая функция тела K в точке P(ξ,η,ζ) в общем случае может быть определена с помощью известного выражения 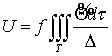[2]:

(2)

здесь - постоянная тяготения; - расстояние точки P(ξ,η,ζ) (рис. 1) от текущей точки P′(ξ′,η′,ζ′); T — объем, занятый телом K. Если обозначить через r и r′ радиус-векторы точек P и P' , через γ — угол между ними, то Δ и γ можно записать в виде , где

. Заметим, что функция потенциала должна удовлетворять ряду требований, которые подробно изложены в монографии [3].

Отметим, что для Земли приняты различные формы записи потенциала притяжения [3], например, стандартная форма, утвержденная комиссией №7 МАС, имеет вид:

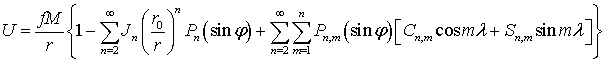. (3)

При численном моделировании используется наиболее общая форма записи:

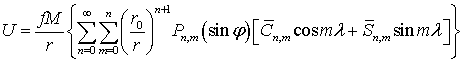, (4)

где:

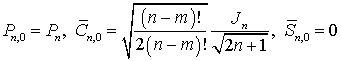. (5)

Следует отметить, что в современных стандартных представлениях геопотенциала коэффициенты не выделяются.

Применение метода вариации произвольных постоянных к уравнениям (1) позволяет записать уравнения движения ИСЗ в оскулирующих элементах. Такие уравнения используются при построении как численных, так и аналитических алгоритмов прогнозирования движения. При численном прогнозировании использование уравнений в оскулирующих элементах обладает тем преимуществом, что невозмущенная часть этих уравнений интегрируется без методических ошибок любым численным методом. Решение уравнений (1) в случае невозмущенного движения имеет вид [4]:

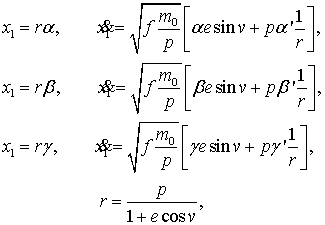(6)

где:

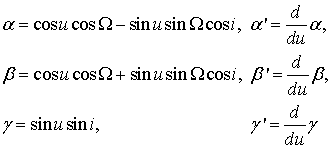
Величины это традиционно используемые элементы Кеплеровой орбиты, т.е.:

· долгота восходящего узла,

· наклонение орбиты к основной координатной плоскости,

· долгота перицентра от узла,

· фокальный параметр,

· её эксцентриситет,

· момент прохождения через перицентр.

Параметры представляют собой направляющие косинусы орбитальной системы координат относительно инерциальной системы, используемой в уравнениях (1). Аргумент широты u определяется формулой , истинная аномалия связана с независимой переменной соотношением:

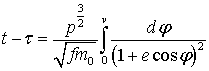(7)

Элементы кеплеровой орбиты являются в формулах (6), (7) постоянными и полностью определены начальными условиями системы уравнений (1).

Если к уравнениям возмущенного движения (1) применить метод вариации произвольных постоянных, в предположении, что решение уравнений (1) сохраняет форму (6), то можно получить совокупность уравнений Ньютона–Эйлера [3]. Наличие эксцентриситета в знаменателе ряда членов в уравнениях Ньютона–Эйлера может приводить к потере точности при исследовании почти круговых спутниковых орбит. В этом случае удобна, например, система уравнений, приведенная в работе [4]:

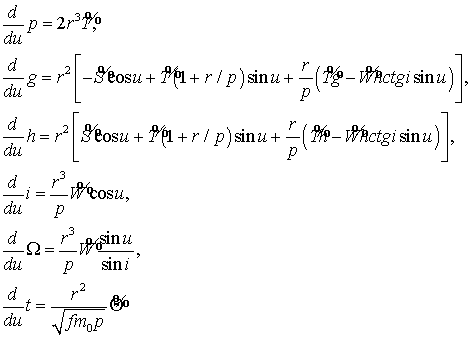(8)

где в качестве независимой переменной выбран аргумент широты, а элементы g и h имеют вид:

Компоненты возмущающего ускорения определяются формулами:

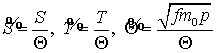, (9)

где

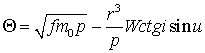. (10)

Отметим, что последнее уравнение в (8) даёт связь оскулирующего и драконического периодов обращения спутника. При построении аналитических и численно-аналитических алгоритмов прогнозирования движения ИСЗ используются также уравнения Лагранжа для оскулирующих кеплеровых элементов, которые связывают изменения элементов с частными производными от возмущающей функции по элементам [4].

251657728 Авторами разработан пакет прикладных программ (ППП), на основе рассмотренных выше соотношений, позволяющий моделировать поведение группировки миниспутников движущихся почти по круговой орбите для задач томографической диагностики параметров атмосферы планеты. Структурная схема данного пакета приведена на рис. 2 а). Программное обеспечение, установленное в вычислительных многопроцессорных модулях каждого спутника должно решать две главные задачи:

· «отслеживать» и «корректировать» отклонения ИС от заданной траектории движения по орбите и «следить» за ориентацией в пространстве самого спутника;

· в соответствующие интервалы времени, благоприятные, с точки зрения геометрии расположения орбитальной группировки, производить замеры лучевых данных при лазерном зондировании с последующим их пересчётом в хордовые данные круговых зон реконструкции.

На рис. 2 а) соответствующие модули ППП выделены пунктирными прямоугольниками – слева показаны модули анализирующие состояние орбиты, скорости спутника его пространственной ориентации и т.д. и вырабатывающие сигналы управления. В правой части изображены программные модули, отвечающие за формирование наборов исходных данных, их нормализацию, процедур реконструкции, анализа реконструированных функций, вычисления погрешностей шумовой составляющей и пр. Последние моменты, связанные с анализом уровня артефактов и зашумлённости восстановленного изображения являются весьма важными, так как дают возможность подобрать параметры процедуры реконструкции для данного метода исследования: способы интерполяции при процедурах доопределения данных, подбор конфигурации ядра, при заданном формате восстановления и т.д. Некоторые результаты в этом плане приведены на рис. 2 б) – исходная модельная функция распределения ионной концентрации в атмосфере, в) – результат неудачной реконструкции (размазанность, дефокусировка, высокий уровень шумовой составляющей), г) – результат реконструкции при автоматическом выборе оптимальных параметров восстановления (свёрточный алгоритм, формат 512´512 элементов).

Так как предполагается, что каждый миниспутник оборудован каналом обмена цифровыми данными с ближайшими соседями и с ОСД, то в такой системе несложно организовать процесс параллельных вычислений, связанных с задачами реконструкции искомых функциональных распределений параметров атмосферы планеты. Именно эта возможность позволяет назвать описанную исследовательскую группировку малых спутников интеллектуальной группировкой, способной самостоятельно решать как задачи навигации, так и задачи реконструкции и передачи информации на основное средство доставки.

Литература

1. Филонин О.В., Талызин Ю.Б. Математическое моделирование процессов исследования планетарных атмосфер с помощью колоний малых спутников, Материалы 3-й Всероссийской н-т конф. «Актуальные проблемы ракетно космической техники» (3 Козловские чтения), Самара, 2013, с. 367 – 371.

2. Аксенов Е.П. Теория движения искусственных спутников Земли. М.: Наука, 1977. 360 с.

3. Т.В. Бордовицина, В.А. Авдюшев Теория движения искусственных спутников Земли, Томск, Издательство ТГУ, 2007, 175 с.

4. Дубошин Г.Н. Небесная механика. Основные задачи и методы. М.: Наука, 1968. 800 с.