Технические науки/11. Робототехника

Д.т.н. Ивель В.П., к.т.н. Герасимова Ю.В.

Северо-Казахстанский государственный университет

им. М.Козыбаева, Казахстан

Адаптивная система управления многодвигательным электроприводом

Одним из элементов современных технологий производства, технического обслуживания и ремонта специализированных грузовых железнодорожных (ЖД) вагонов является возможность их вращения и подъема на заданный угол и высоту. В частности при производстве вагонов-зерновозов при сборке полувагона и крыши полувагона необходимо поворачивать их вокруг горизонтальной оси.

Цель предлагаемой работы заключается в разработке компьютерной системы управления вращением-подъемом ЖД вагонов с возможностью адаптации к внешним силовым нестационарным воздействиям т.е. к переменным моменту инерции и моменту сопротивления, что позволит значительно усовершенствовать технологический процесс, снизить затраты на производство и ремонт ЖД вагонов.

Известна система управления многодвигательным электроприводом многосекционных агрегатов [1], которая может быть использована во взаимосвязанных приводах постоянного и переменного тока агрегатов по перемещению полосовых материалов. Основной недостаток данной системы – низкая стабильность второго привода при изменяющихся параметрах объекта. Более совершенной можно считать систему управления многодвигательным электроприводом многосекционных агрегатов [2].

Принцип работы данной системы основан на использовании дополнительных блоков, повышающих стабильность работы системы второго привода и обеспечивающих быстродействие и устойчивость исходной системы привода. Однако и здесь присутствуют существенные недостатки – невозможность сохранять высокую точность заданного отклонения угла поворота вала второго привода от угла поворота вала первого привода и поддерживать оптимальное быстродействие, поскольку в системе управления отсутствуют датчики измерения угла поворота валов приводов и не учитывается нестационарность постоянных времени приводов.

С целью устранения описанных недостатков предлагается адаптивная система управления многодвигательным электроприводом, основанная на использовании дополнительных блоков, позволяющих повысить быстродействие системы в переходных и точность в установившихся режимах.

Система состоит из двух идентичных контуров (рис 1), каждый из которых включает регулятор скорости (РСк), состоящий из сумматора С и пропорционально-дифференцирующего звена (ПД), усилителя мощности (УМ), асинхронного электродвигателя (ЭД), редуктора (Р), рабочего механизма (РМ), дифференциатор (Д) и датчик угловых перемещений (ДУ). Кроме того, система содержит задачик угловой скорости (ЗСк) и задатчик углового смещения (ЗУС), интегратор (Инт), идентификатор (Ид) и блок электронной модели.

Система управления работает следующим образом.

Объектом управления являются два взаимосвязанных электропривода, первый из которых является ведущим, а второй ведомым. Скорость вращения валов которых должна сохранять заданное задатчиком ЗСк значение ω_ЗД. Углы поворота φ₁ и φ₂ валов измеряются датчиками угловых перемещений ДУ1 и ДУ2, преобразуется с помощью дифференциаторов Дф1 и Дф2 в угловые скорости ω₁ и ω₂, которые в узлах суммирования С1 и С2 вычитаются из ω_ЗД. Отклонения ∆₁= ω_ЗД – ω₁ и ∆₂= ω_ЗД – ω₂ поступают на корректирующие пропорционально-дифференцирующие звенья ПД1 и ПД2 и затем, усиленные силовыми преобразователями УМ1 и УМ2, – на электродвигатели ЭД1 и ЭД2. Вращение валов электродвигателей через редукторы Р1 и Р2, передается на рабочие механизмы РМ1 и РМ2, например, валы прокатных станов или механизмы поворота железнодорожных вагонов.

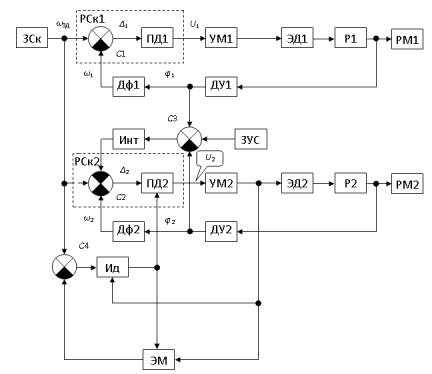
Рисунок 1. Структура адаптивной системы управления

Зависимость между напряжением питания (выход корректирующего звена) U и скоростью вращения вала рабочего механизма ω можно представить следующим линеаризованным дифференциальным уравнением

, (1)

где Т_ЭП – постоянная времени;

k – коэффициент усиления.

С помощью известных преобразований передаточную функцию электропривода (ЭП) как объекта управления можно представить в следующем виде:

, (2)

где - оператор дифференцирования.

Таким образом, чтобы компенсировать инерционность привода целесообразно в качестве корректирующего звена выбрать пропорционально-дифференцирующее звено с передаточной функцией

, (3)

где Т_К выбирается равной Т_ЭП.

Кроме того, чтобы поддерживать определенное заданное соотношение φ_ЗД между углами поворота φ₁ и φ₂ валов ведущего и ведомого привода в систему введен сумматор С3 и задатчик этого соотношения ЗУС. В случае использования в качестве рабочих механизмов механизмы поворота железнодорожных вагонов соотношение φ_ЗД задается равным нулю для устранения перекосов и дополнительных нагрузок в работе рабочих механизмов. Сумматор который вычисляет реальную разность в углах поворота и заданным значением φ₁ – φ₂ – φ_ЗД. Затем этот суммарный сигнал с выхода сумматора С3 через интегратор поступает в качестве обратной отрицательной связи на сумматор С2. Таким образом, поддерживается высокая точность в регулировании заданного отклонения угла поворота вала ведомого привода от угла поворота вала ведущего привода.

Однако трудность в поддержании высокого качества и быстродействия в управлении ведомым приводом заключается в том, что параметр Т_ЭП в формуле (1) заранее неизвестен, может зависеть от многих факторов, не может быть измерен и в общем случае представляет собой нестационарную величину. Поэтому в данной системе предусмотрена автоматическая настройка параметра Т_К в передаточной функции (3) по динамическим характеристикам электропривода с помощью их электронных моделей и блока идентификации [3].

Блок идентификации описывается уравнением

, (4)

где J является функционалом оптимизации и в данном случае принято

, (5)

здесь ε(t) – сигнал рассогласования между выходами ЭП и эталонной модели ЭП.

Компоненты градиента функционала (5) определяются по обычному правилу дифференцирования сложной функции:

. (6)

Представим критерий оптимизации (5) в следующем виде

, (7)

здесь добавлен множитель 1/2 для удобства дальнейших преобразований, а черта символически обозначает операцию усреднения во времени. Уравнение (6) с учетом (7) примет вид

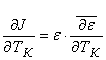. (8)

Градиентный алгоритм настройки параметра Т_К из условия достижения минимума функционала J(ε) можно представить в следующем скалярном виде:

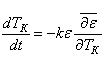(9)

или

.

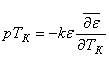Другими словами, движение к оптимальному значению J производится по градиенту в сторону его оптимального значения со скоростью, пропорциональной градиенту J.

Определяется сомножитель в выражении (9) следующим образом

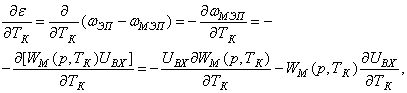(10)

где ω_ЭП – выходной сигнал текущей угловой скорости ЭП, ω_МЭП – выходной сигнал модели ЭП, W_М(p,Т_К) – передаточная функция электронной модели ЭП, U_ВХ – сигнал на входе ЭП.

Так как , то уравнение (10) можно упростить

, (11)

где - вспомогательный оператор.

Таким образом, определяя параметр Т_К и используя его в алгоритме настройки передаточной функции пропорционально-дифференцирующего звена (3), можно с достаточной достоверностью добиться приближения передаточной функции системы управления к пропорциональному звену, что, в свою очередь, приведет к оптимальному соотношению точности и быстродействию системы управления многодвигательным электроприводом.

Литература:

1. Патент РФ № 2386740, D21F 7/02, опубл. 20.04.2010.

2. Патент РФ № 2456740, H02P5/00, D21F7/02, опубл. 20.02.2012

3. Чураков Е.П. Оптимальные и адаптивные системы: Учеб. пособие для вузов. – М.: Энергоатомиздат, 1987. – 256 с.: ил.