Доповідь/Технічні науки – Автоматизовані системи управління на виробництві

Д.т.н. Семенцов Г.Н., Гутак О.В., Кизима Л.В.

Івано-Франківський національний технічний університет нафти і газу

Оцінка автокреляційної функції сигналу давача механічної швидкості буріння і її апроксимація

Визначення оцінок автокреляційної функції сигналу давача механічної швидкості буріння є актуальною науково-прикладною задачею для автоматичного регулювання параметрів режиму буріння та їх оптимізації. Ці оцінки необхідні для вибору кроку дискретизації, синтезу алгоритмів непрямих вимірювань, діагностування технічного стану породоруйнівного інструменту, оцінки ефективності процесу та ін.

Проте, аналіз літературних джерел (наприклад, [1÷3] та ін.) вказує на недостатній обсяг проведених досліджень в контексті використання сучасного програмного забезпечення і формальних критеріїв оцінки адекватності отриманих моделей кореляційних функцій.

Тому метою даної роботи є отримання адекватної автокореляційної функції сигналу давача механічної швидкості буріння на основі експериментально отриманої реалізації досліджуваного процесу.

Сигнал давача механічної швидкості буріння V(t) є непрямим показником ефективності процесу буріння нафтових і газових свердловин і використовується у схемах регулювання подачі долота на вибій свердловини.

На відрізку реалізації V(t) (рис.1) тривалістю Т=100хв, отриманої у процесі буріння свердловин в умовах Прикарпаття визначено інтервал квантування Δt ≤ 0,5 Т_вч, де Т_вч – період найвищої гармонічної складової випадкового сигналу V(t) [1] та база даних у кількості 100 точок для дослідження.

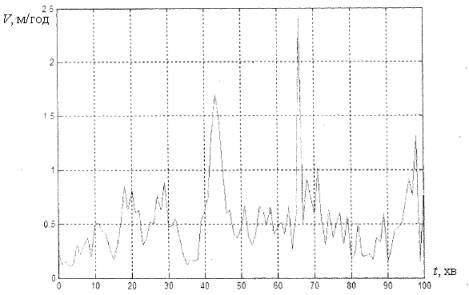
Рисунок 1 – Графік зміни величини V(t), отриманий у результаті оброблення експериментальних даних у програмі Mathlab

Оскільки реалізація V(t) є сукупністю дискретних значень сигналу, отриманих через рівні проміжки Δt, то автокреляційну функцію розрахуємо за формулою [1]:

_,

де х⁰(t)= х(t)–m_x – центровані значення.

Визначення кореляційної функці:

Rxx = xcorr(x,x, ‘none’);

Rxx = Rxx/max(Rxx);

tt = -100:1:100;

figure

plot (tt, Rxx, tk, yf), grid.

Особливості процесу буріння дали змогу прогнозувати характер автокореляційної функції, внаслідок чого, як апріорну обрали модель такого типу [2]

_{, (1)}

_{де a, b, c, d, f, g, α, β – параметрі моделі,}

_{τ – кореляційний зсув.}

Оцінку автокреляційної функції R_vv(τ) розраховано з кореляційним зсувом τ = 1 хв (рис.2).

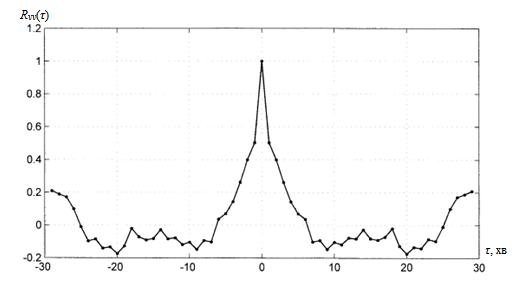
Рисунок 2 – Графік автокреляційної функції R_vv(τ)

Апроксимацію графіка нормованої автоореляційної функції проведено з використанням програми Curve Expert 1.3. У результаті отримали математичні моделі, що наведені у табл. 1. Вони мають різні коефіцієнти кореляції і стандартні похибки, графіки залежності яких від порядку поліномів n, наведено на рис.3.

Таблиця 1 – Моделі нормованої автокореляційної функції механічної швидкості буріння R_vv(τ)

Тип мо-делі	Модель нормованої автокореляційної функції Rvv(τ)	Похибка апрокси-мації, SE	Коефіцієнт кореляції, Cor
А	Rvv(τ)=0,7075-0,16245τ+0,009006τ^2-0,00014τ^3	0,111	0,900
В	Rvv(τ)=0,8916-0,3186τ+0,0351τ^2-0,0016τ^3+2,6227е^-0,005 τ^4	0,062	0,972
С	Rvv(τ)=0,9708-0,4306τ+0,0651τ^2-0,0045τ^3+0,0001τ^4- -1,6916е^-0,006 τ^5	0,045	0,986
D	Rvv(τ)=0,9398-0,3601τ+0,0373τ^2-0,0004τ^3+0,0001τ^4+ +7,18846е^-0,006 τ^5+1,05716е^-0,007 τ^6	0,0421	0,988
E	Rvv(τ)=0,99654-0,4526τ+0,0881τ^2-0,011τ^3+0,0009τ^4- -4,85576е^-0,005 τ^5+1,3387е^-0,006 τ^6-1,47е^-0,008 τ^7	0,037	0,991
F	Rvv(τ)=0,981-0,5469τ+0,1574τ^2-0,0304τ^3+0,0036τ^4- -0,0002τ^5+9,8718е^-0,006 τ^6-2,0147е^-0,007 τ^7+1,6717е^-0,009 τ^8	0,350	0,992
G	Rvv(τ)=0,988-0,607τ+0,2151τ^2-0,0511τ^3+0,0079τ^4- -0,0006τ^5+3,2992е^-0,005 τ^6-1,016е^-0,006 τ^7+1,7157е^-0,008 τ^8+ +1,2289е^-0,01 τ^9	0,034	0,993
H	Rvv(τ)=0,994-0,7121τ+0,33951τ^2-0,1069τ^3+0,0201τ^4- -0,0023τ^5+0,0001 τ^6-7,7588е^-0,006 τ^7+2,2125е^-0,007 τ^8- -3,549е^-0,009 τ^9+2,4471е^-0,011 τ^10	0,033	0,994

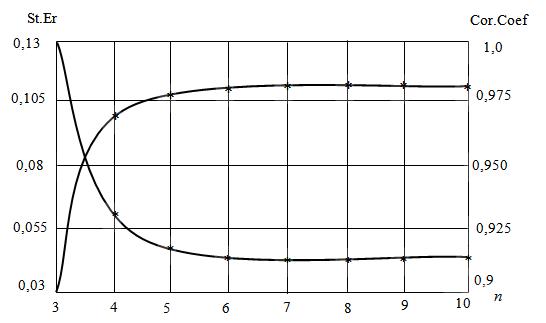
Рисунок 3 – Графік залежності похибки апроксимації St.Er і коефіцієнта кореляції Cor.Coef від порядку n поліному апроксимації автокореляційної функції механічної швидкості буріння R_vv(τ)

Аналізування графіків, наведених на рис.3, показало досить добре співпадання експериментальної оцінки R_vv(τ) з апріорною моделлю спостерігається, починаючи з поліному шостого порядку (n =6).

Проте, аналіз графіків апроксимації функцій довів, що найбільш адекватним є поліном 8^th Degree Polinomial Fit.

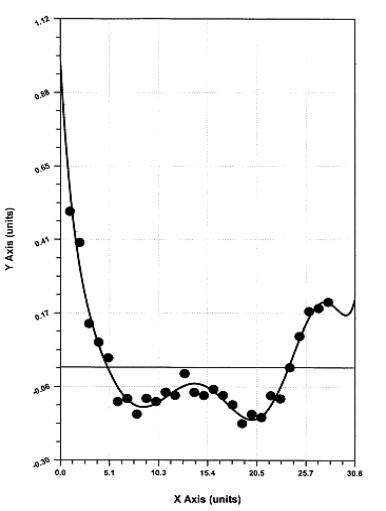
Рисунок 4 – Графік апроксимації оцінки кореляційної функції поліномом 8-го порядку

Коефіцієнти цього рівняння мають такі значення:

8^th Degree Polinomial Fit: у=а+bх+сх^{^}2dx^{^}3...

Соеffісіеnt Data:

a =0.95170541; b=-0.54691313; c=0.15749174; d=-0.030448054;

e=0.0036208858; f=-0.00025157315; g=9.8718І93е-006;

h = -2.0197104е-007; i=1.671713е-009.

8^th Degree Polinomial Fit: у=а+bх+сх^{^}2dx^{^}3...

Standart Еrrоr: 0.0350197

Correlation Соеffісіеnt: 0.9929720

Соmments:

Linear regression completed successfully. No weighting used.

Висновок

Досить добре спів падання експериментальних оцінок автокореляційної функції механічної швидкості буріння з апріорною моделлю не потребує уточнення довжини досліджуваної реалізації. Окрім цього впливом похибки від дискретизації на точність оцінки ординат автокореляційної функції також можна знехтувати.

Література:

1. Назаренко М.В. Теоретичні засади та принципи побудови моделей динамічних процесів та їх регуляторів: [монографія] /М.В.Назаренко. – Кривий Ріг: Діоніс (ФОП Чернявський Д.О), 2010. – 204 с.

2. Волгин В.В. Оценка корреляционных функций в промышленных системах управления / В.В.Волгин, Р.Н.Каримов. – М.: Энергия, 1979. – 80 с.

3. Горбійчук М.І. Оптимізація процесу буріння глибоких свердловин / М.І.Горбійчук, Г.Н.Семенцов. - Івано- Франківськ: Факел, 2003. - 493с.