К.т.н. Пунин В.И., МГТУ им. Н.Э. Баумана, Россия.

Д.т.н. Кохан Л. С., Университет Машиностроения, Россия.

Эффект укорочения полосы при гибке

Производственная практика изготовления гнутых профилей как из мерной, так и «бесконечной» заготовки на профилегибочных станах свидетельствует о малозаметном, но стабильном изменении длины заготовки после её прокатки. В многоклетьевых станах натяжение полосы (профиля) между клетями может создаваться и регулироваться изменением окружных скоростей валков соседних клетей (например, благодаря увеличению формующих диаметров), либо изменением зазоров между валками последующих клетей, в результате обусловливающих возникновение заднего ξ₀ и переднего ξ₁ натяжений. Создание натяжения заготовки в валках соседних клетей, расположенных на расстоянии L между собой, при определенных условиях может привести к тому, что возможное различие между растягивающим и подпирающим действием усилий Т₀ и Т₁ может привести к потере устойчивости и «выпучиванию» полосы (рис. 1). При этом увеличивается суммарная волнистость полосы в каждой последующей клети, что существенно влияет на фактическую длину.

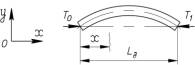
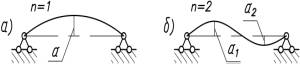
Рис.1. Схема нагружения и потери устойчивости полосы: а) – одна дуга, б) – две дуги

Величина данной продольной деформации при малых прогибах может быть определена с известными допущениями по методу Л.Эйлера с использованием дифференциального уравнения: . Разделив обе части уравнения на EJ и обозначив T/EJ через k², приводим его к виду . Здесь Е – нормальный модуль упругости материала полосы; J – момент инерции полосы; Т = (1 – ξ)σ_тbS – усилие натяжения/сжатия; S, b – толщина и ширина полосы; σ_т – сопротивление пластической деформации. После этого можно определить неизвестный параметр: . Решение дифференциального уравнения 2-го порядка, устанавливающего величину выпучивания, имеет следующий вид: y = asinkx = 0.

В процессе прокатки прогиб полосы под валками, например, первой клети отсутствует, т.е. y = 0. Аналогично для второй клети y = asinkL = 0, откуда следует k = πn/L_д.

Подставляя параметр k, определим действующее натяжение: , где n – число дуг на контуре (рис. 1). При наименьшем значении (n = 1) критическое натяжение

или , откуда .

Соответственно, прогиб полосы при n = 1 и x = L/2 : y = asin(πx/L_д).

Далее, в зависимости от характера «выпучивания», максимальный прогиб полосы y_max = a при n = 1 и x = L/2 , y_max = a₁ = a₂, при n = 2 и x = L/4. При моменте инерции полосы J=bS³/12 устанавливается прогиб :

,

где χ – коэффициент, зависящий от материала и геометрии профиля. Для стали χ ≈ 0,1.

Например, в случае прокатки в стане с межклетьевым расстоянием L = 200 мм полосы толщиной S = 2,0 мм (L/S = 100) с сопротивлением пластической деформации σ_т = 40 МПа, модулем упругости E = 1,4·10⁵ МПа и при натяжении ξ = 0,8 величина выпучивания равна: мм.

На основании полученной формулы рассчитаем изменение длины полосы при прокатке с натяжением. Для исследуемого случая длина дуги равна:

мм,

откуда уменьшение длины полосы на этом участке ΔL' = L_д = 200,109 – 200 = 0,109 мм.

Для 10-клетьевого профилегибочного стана (m = 10), уменьшение длины полосы на девяти участках деформирования составит ΔL = (m – 1)ΔL' = (10 – 1)0,109 = 0,981 мм.

В условиях промышленного производства гнутого профиля, предназначенного для изготовления противопожарных дверей было зафиксировано укорочение заготовки в рабочих клетях стана, которое возрастало с увеличением числа клетей. На «бесконечной» полосе до ее задачи в стан наносили риски на участке определённой длины, расстояние между ними фиксировали и сравнивали со значением, измеренным после профилирования полосы. Аналогичные расчеты при других параметрах натяжения ξ представлены ниже:

Ξ	0,8	0,6	0,5
a, мм	2,857	5,714	7,143
ΔL, мм	0,981	3,915	6,111

Таким образом, происходящие при формообразовании полосы в клетях деформационные процессы сопровождаются уменьшением ее длины в зависимости от натяжения, числа клетей и отношения межклетьевого расстояния к толщине заготовки.