УДК 532.5:621.16
К.т.н. Ысқақ Е.Н., магистр т.н. Бектас Д.Б., к.т.н.
Абильдаев Н. А.
Кызылординский
государственный университет имени Коркыт Ата
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ ПРОЦЕССОВ МНОГО ФАЗОВЫХ СРЕД В
ТЕПЛОМАССООБМЕННЫХ АППАРАТАХ
Во многих отраслях отечественной
промышленности для организации массообмена между обрабатываемыми потоками наиболее
эффективными показали себя колонные массообменные аппараты с регулярным
расположением неподвижных и подвижных насадок благодаря низкому гидравлическому
сопротивлению, возможности обработки больших объемов газа и жидкости.
В
колонных массообменных аппаратах вообще, и в аппаратах с регулярными насадками,
где в частности - основным обрабатываемым потоком является газовый поток.
Теоретические и экспериментальные данные многочисленных авторов, работающих в
таких областях, как механика жидкости и газа, химическая технология, энергетика
и т.д. показали, что наиболее информативными являются такие характеристики
динамики газа, как скорость и давление. Знание этих величин, закона их
распределения по объему всего аппарата позволяют определить практически все
качественные и количественные показатели- вихревые и застойные зоны,
гидравлическое сопротивление, диссипативную функцию и т.д. Чаще в литературе
встречаются достаточно полные данные по математическому моделированию обтекания
тел различных форм в ламинарном и турбулентном режимах.
Однако, основными уравнениями,
описывающими движения газа или жидкости в предложении несжимаемости для
плоского случая, является система уравнений Навье-Стокса, содержащая два
уравнения количества движения и уравнение неразрывности:
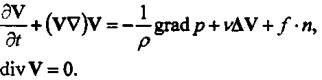 (1)
(1)
В системе уравнений (1) искомыми функциями являются вектор
скорости V, давление р, которые зависят от пространственных координат и времени t. Параметрами будут плотность р, коэффициент кинематической вязкости V ( - коэффициент динамической вязкости), силовая функция
ƒ, единичный вектор n.
Первое из уравнений в системе (1),
представляющее собой систему из трех уравнений для проекции вектора скорости V(u,v,w), называемое уравнением
количества движения, представляет собой баланс между силами инерции, силами
давления, трения и массовыми силами. Второе из уравнений системы (1) является уравнением неразрывности.
Система (1) позволяет
при заданных в некоторый момент времени tо значениях полей искомых функций V,p и соответствующих граничных условиях определить
значение полей этих функций в момент времени tо+τ, где τ>0. Движение жидкости в аппарате, описываемое системой (1), осуществляется либо
благодаря действию массовых сил, либо действию внешних сил, создающих перепад
давления ∆р. Частным случаем системы уравнений (1) является система уравнений движения газа в декартовой
системе координат х,у:
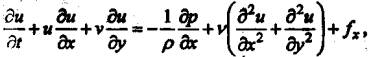 (2)
(2)
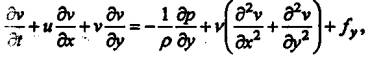 (3)
(3)
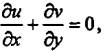 (4)
(4)
Где р-давление, Па
U,v-состовляющие вектора
скорости по направлениям координат, м/с;
V-динамический коэффициент вязкости, м2/с;
Х,у-направления координат по вертикали и
горизонтали, соответственно, м;
t-время, с.
В зависимости
от конкретной физической ситуации различаются следующие виды граничных условий:
1. Граничные условия на непроницаемой
твердой поверхности аппарата San,
называемые
условиями прилипания. Если обозначить скорость движения поверхности аппарата
через то граничное условие на этой поверхности будет иметь вид
![]() (5)
(5)
Наиболее
часто в различных процессах встерчается обтекание неподвижной твердой стенки
аппарата, когда Vc=0.
2. Граничное условие вдали от обтекаемого
тела, имеющее асимптотический
характер:
![]() (6)
(6)
где r-расстояние
от поверхности обтекаемого тела.
3.
Периодические граничные условия, представляющие специальный тип граничных
условий, которые обычно ставятся при обтекании бесконечной последовательности
повторяющихся тел. При этом параметры потока перед телом равны параметрам
потока за телом:
V1 = V2. (7)
4.Условия симметрии, так же как
периодические условия, представляющие специальный тип граничных условий,
возникающих вследствие определенных предположений о свойствах симметрии
течения. Например, при обтекании симметричного профиля равномерным потоком
граничным являются следующие условия на оси симметрии:
![]() (8)
(8)
где
ν-составляющая скорости по нормали к оси симметрии. В определенном
диапазоне режимных параметров эти условия могут соответствовать реально
наблюдаемым течениям, однако во многих случаях их постановка существенно сужает
класс возможных движений и взаймодействий так же, как и постановка условий (7).
5. Граничные условия на поверхности раздела двух фаз в случае, когда эта
поверхность фиксирована, и трением в одной из сред можно пренебречь
![]() (9)
(9)
что аналогично условиям
симметрии(8).
Уравнения (2)-
(4) вместе с начальными условиями
![]() (10)
(10)
для полей
скорости и давления и соответствующими граничными условиями представляют
замкнутую систему, позволяющую определить поля скорости и давления однородной
несжимаемой вязкой жидкости и их изменение во времени. Однако система уравнений
(2)-(4) с уравнением неразрывности (4) неудобна для проведения вычислений и
может быть заменена эквивалентной системой. Для этого можно продифференцировать
уравнение (2) по х, уравнение (3) – по у и сложить результаты, используя при последующих
преобразованиях уравнение (4). Тогда получим
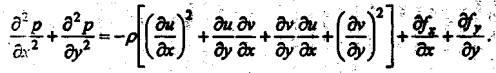 (11)
(11)
Система
уравнений (2), (3), и (11) представляет одну из разновидностей уравнений Навье - Стокса в переменных скорость, давление, используемую в
вычислительной практике.
Уравнения (2)
- (4) могут быть записаны в иной форме, не содержащей давления и в ряде случаев
более удобной для численной реализации. В декартовых координатах эта система
записывается в следующем безразмерном виде:
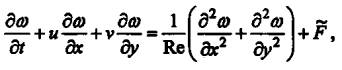 (12)
(12)
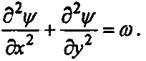 (13)
(13)
Здесь ![]() , где
, где
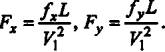 Функция тока
и вихрь заданы соотношениями
Функция тока
и вихрь заданы соотношениями
![]() (14)
(14)
![]() (15)
(15)
Общее решение
задачи (2) - (4) представляет собой одну из сложных задач математики и механики
и до сих пор не достаточно изучены. Поэтому эта задача, исходя из конкретных
условий исследования, упрощается, и находятся аналитические,
приближенно-аналитические или численные решения. Например для задачи обтекания
пластины, предполагается, что скорость газа во всем потоке не меняется,
следовательно, давление и скорость не меняются по х. Уравнение Прандтля в
этом случае будет иметь вид:
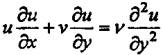 , (16)
, (16)
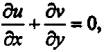
а граничные
условия запишутся следующим образом
![]() (17)
(17)
Показано,что решение задачи (16)
с (17) может быть сведено к решению краевой задачи для обыкновенного
дифференциального уравнения.
Обработкой численного решения
найдено автомодельное решение в виде
![]() (18)
(18)
![]() - функция, зависящая от автомодельной
переменной
- функция, зависящая от автомодельной
переменной 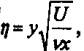 где параметр
где параметр ![]() найден методом наименьших квадратов.
найден методом наименьших квадратов.
При
исследовании различных задач гидродинамики и массообмена применяется метод
интегральных соотношений. Основная идея этого метода состоит в том, что вместо
точных распределений скоростей в сечениях пограничного гидродинамического слоя
применяется некоторый набор профилей, представленных семейством кривых с одним
параметром. Изменение параметра создает то разнообразие профилей, которое
необходимо для приближенного описания движения во всем пограничном слое. Этот
параметр, иногда его называют «формпараметром», представляет собой функцию
продольной координаты в пограничном слое. Для определения этого параметра
выведено интегральное условие, которое является результатом применения теоремы
импульсов к элементарному объему пограничного слоя и называется иногда
уравнением импульсов. Предполагается, что жидкость несжимаемая, движение
установившееся, потоки изотермичны. Тонкий слой жидкости движется без
волнообразования по спирали Архимеда, уравнение спирали в полярных координатах r, θ имеет вид r = Aθ, A > 0.
Предполагается, что градиент давления в слое создается только за счет вращения.
Система координат x, y связана с обтекаемой твердой поверхностью, ось x направлена
вдоль потока, y – по нормали к
потоку. При этих предположениях движение тонкого слоя жидкости можно описать
уравнениями Прандтля:
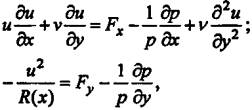 (19)
(19)
![]()
R(x) – радиус
кривизны в полярных координатах:
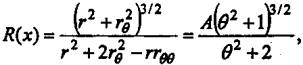 (20)
(20)
где ![]() проекции массовых сил на оси x и y
соответственно. Эта система уравнений может быть решена методом интегральных
соотношений.
проекции массовых сил на оси x и y
соответственно. Эта система уравнений может быть решена методом интегральных
соотношений.
Заключение
Приведен некоторый математический анализ
особенностей работы колонных массообменных аппаратов с регулярными насадками.
Получено приближенно-аналитическое автомодельное решение, где предполагается,
что скорость газа во всем потоке не меняется.
Литература
1.
Балабеков О.С. Гидродинамика, массообмен и пылеулавливание при
противоточных и прямоточных двухфазных капельных и пленочных течениях в слое
подвижной насадкой: автореф. дис. д-ра техн. наук-М..1985-40с.
2.
Валедберг А.Ю., Савицкая
Н.М. Охлаждения газов в скрубберах промышленная и санитарная очистка
газов.М.:ЦИНТИХимнефт,1986-38с.
3.
А.С. № 1098117 СССР, МКИ
В 01 Д53/20. аппарат с насадкой / Петин В.Ф., Волненко А.А., Балабеков О.С. и
др. (СССР).-6с.: ил.
4.
Броунштейн Б.И., Шегелов
В.В. Гидродинамика, массо - и теплообмен в колонных
аппаратах.-Л.: Химия, Л.О., 1988.-335с.
5.
Рамм В.М. Абсорбция
газов. 2-е изд. перераб и доп.-М.: Химия, 1976.-656с.