к.т.н.
Звонов С. Ю., к.т.н. Шляпугин А. Г., Цыцорин Д. С.
Федеральное государственное бюджетное образовательное учреждение высшего
профессионального образования «Самарский государственный аэрокосмический
университет имени академика С.П. Королева (национальный исследовательский
университет)»
Применение
ANSYS/LS-DYNA в моделировании гибки сотовой панели
Требования,
предъявляемые к современным летательным аппаратам (ЛА) по уровню шума, в
настоящий момент ограничивают возможность использования отечественных самолетов
в ряде европейских стран [1].
Одним из
перспективных методов снижения уровня шума, производимого двигателем ЛА,
является использование звукопоглощающих панелей (ЗПК) [2].
Конструктивно
ЗПК изготавливаются из сотового заполнителя, заключенного между двумя листами
металла, один из которых имеет отверстия для проникновения звуковых колебаний.
Гашение колебаний осуществляется в ячейках сотового заполнителя.
В качестве
материала панелей используются титановые сплавы. Сотовый заполнитель
изготавливают из технического титана ВТ1-0, обладающего высокой прочностью при достаточной пластичности и вязкости,
высоким сопротивлением малым пластическим деформациям, хрупкому и усталостному
разрушению.
В качестве материала обшивок используются листы из сплава ОТ4-1 и 12Х18Н10Т.
Отличительной
особенностью изготовления данной конструкции является низкий коэффициент
использования материала, высокий процент брака и значительная трудоемкость. В
связи с чем, очевидно, что интенсификация процесса изготовления ЗПК является перспективным
направлением в производстве ЛА.
Проведение
исследования на реальной модели в данном случае не целесообразно в виду высокой
стоимости материала и трудоемкости изготовления панели. В связи с тем, что в
настоящий момент нет разработанных методик использования программного
обеспечения для моделирования процесса изготовления сотовых панелей целью
работы, является оценка перспективы использования программного продукта LS-DYNA
для расчета данной задачи.
Типовой
технологический процесс изготовления ЗПК включает следующие основные операции:
изготовление гофрированной ленты, по форме соответствующей половине ячейки соты; сборка панели ЗПК;
придание панели окончательной формы на гибочно-растяжном прессе.
 а)
а)  б)
б)  в)
в)
а)
– продольные складки, б) – поперечные складки,
в)
– разрыв наружной обшивки
Рис.
1. Дефекты, возникающие при гибке ЗПК
Виды брака,
возникающие при гибке ЗПК, приведены на рисунке 1. В-первых двух случаях
причиной возникновения брака является наличие сжимающих напряжений в НДС. В
третьем не соблюдение режимов сварки.
Причина
возникновения продольных складок (рисунок 1а) в настоящее время не изучена. Для
проведения исследований необходимо создание масштабной модели, что не может
быть выполнено на практике из-за большого различия габаритов детали и толщины
материала. Проводить исследования на реальной модели не целесообразно в виду
высокой стоимости и трудоемкости изготовления панели. Выходом из данной
ситуации является использование вычислительного эксперимента.
Для описания поставленной задачи использовалась программа ANSYS/LS-DYNA [3,4].
При моделировании процесса применялись оболочечные
конечные элементы. Для решения задачи был выбран элемент с формулировкой SHELL
163 – оболочечный элемент с 4 узлами, возможностью изгиба и пружинения. Элемент
имеет 12 степеней свободы в каждом узле.
В качестве модели материала заполнителя и обшивок
использовалась билинейная изотропная (Bilinear Isotropic). При
задании материала инструмента – твердое тело (rigid) – указывалось, что модель
с данными свойствами будет неподвижна.
Геометрическая
модель была построена в ANSYS, так как импорт из CAD-системы
вызывал трудности, связанные с наложением поверхностей, образованием зазоров,
перекрытием (взаимным внедрение частей геометрической модели).
В связи с
необходимостью описания задачи большим числом конечных элементов было принято
решение упростить геометрию заполнителя, заменив рифтованные грани имеющие в
сечении швеллер прямолинейными отрезками (рисунок 2а.б).
При дискретизации геометрической модели использовалось
упорядоченное разбиение на четырехугольные элементы.
Задание
контактных поверхностей осуществлялось автоматически с коэффициентом трения 0.12,
тип контакта Single Surface Automatic
(ASSC).
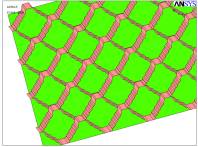 а)
а)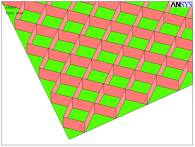 б)
б)  в)
в)
а) – точная модель заполнителя, б) – упрощенная модель
заполнителя,
в) – окончательный вид модели
Рис. 2. Допущения при построении геометрии
и окончательный вид модели
В виду
симметричности задачи была построена только половина геометрии заготовки и
инструмента. При наложении граничных условий были определены условия симметрии:
запрет перемещения вдоль оси Оx и запрет вращения
относительно осей Оy и Оz.
Рассчитывались
два варианта задачи. В первом варианте в качестве кинематических параметров процесса
были заданы усилие и время. Графики изменения усилия по координатам x и z в
зависимости от времени показаны на рисунке 3.
Во втором
варианте в качестве параметров процесса были заданы полученные из результатов
первого варианта значения перемещения и времени участков торца заготовки
помещаемого в зажимы пресса.
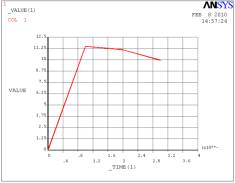 а)
а) 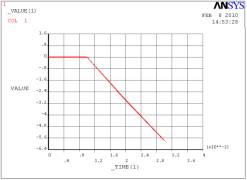 б)
б)
а)
– усилие по координате x, б) – усилие по
координате z
Рис.
3. Графики изменения усилия процесса
Для
параметров перемещения инструмента были заданы координаты ключевых точек: в
первоначальном положении, в момент предварительного растяжения, в момент гибки
на 15°, в момент перед доворотом зажимов, в момент после доворота и в
окончательный момент операции гибки.
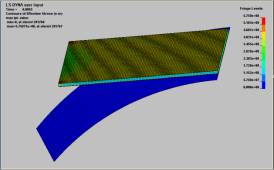
Для
просмотра результатов расчета использовался постпроцессор LS-PREPOST
2.1(рисунок 4). Проведенный вычислительный эксперимент показал, что при
предварительном растяжении происходит равномерная деформация всей пластины.
После начала гибки, возникают зоны со значением напряжений по Мизесу равных
нулю. Эти зоны могут являться очагами образования складок. Что подтверждено на
практике (рисунок 1).
 а)
а) б)
б)
а)
– растяжение; б) – заключительный момент гибки
Рис.
4. Значения напряжений при гибке
Исходя из
этого, было сделано предположение о том, что образование складок происходит
из-за недостаточных предварительных растягивающих напряжений.
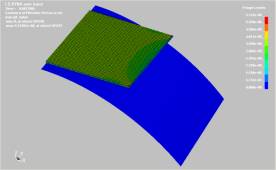
Также
проводился вычислительный эксперимент, где была описана неравномерная фиксация
заготовки захватами в центральной части. В ходе расчета было установлено, что
при таких условиях в заготовке возникают неоднородные зоны напряжений,
показанные на рисунке 5. На основании чего можно сделать вывод, что равномерный
захват заготовки может привести к образованию складок как продольных, так и
поперечных, что также подтверждено на практике (рисунок 1).
 а)
а) б)
б)
а)
– начальный момент гибки; б) – заключительный момент гибки;
Рис.
5. Распределение напряжений при неравномерном захвате заготовки
Помимо этого
вычислительный эксперимент показал неплотное прилегание панели к инструменту.
Плотный контакт осуществляется только в средней части ширины панели (рисунок 6).
Что также подтверждается практикой и приводит к увеличению припуска по ширине.
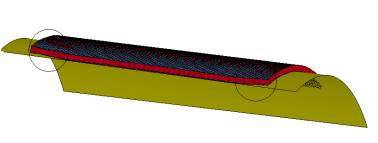
Рис.
6. Контакт заготовки и инструмента
Заключение:
проведенное моделирование процесса гибки сотовой панели показало, что использование
программного продукта LS-DYNA позволяет получить достоверную картину
деформирования сотовой панели.
СПИСОК
ИСТОЧНИКОВ
1. Дмитриев,
В.Г. Полет: Программа снижения шума отечественных самолетов [Текст]/В.Г.
Дмитриев, А.Г. Мунин, В.Ф.Самохин, 09.2003.–7-13 с.
2. Дмитриев,
В.Г. Полет: Проблема авиационного шума на местности – состояние и перспективы /
В.Г. Дмитриев, А.Г. Мунин, В.Ф. Самохин, 11.2000. –13-21 с.
3. Ansys в
руках инженера : Практическое руководство / Каплун А.Б., Морозов Е.М.,
Олферьева М.А. – М. : Едиториал УРСС, 2003. – 272с/
4. Ansys
для инженеров: Справочное пособие /
Чигарёв А.В., Кравчук А.С., Смалюк А.Ф. – М. : Машиностроение, 2004. – 512с.