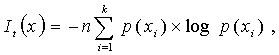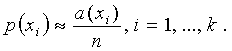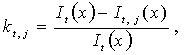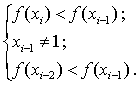Д.т.н. В.В. Мартынов, Е.С. Плешакова

Саратовский государственный технический университет

имени Гагарина Ю.А., Россия

АЛГОРИТМИЗАЦИЯ ПРОЦЕССА

ИДЕНТИФИКАЦИИ РАСПРЕДЕЛЕНИЯ ДАННЫХ

О СВОЙСТВАХ МОДИФИЦИРОВАННОГО

РЕЖУЩЕГО ИНСТРУМЕНТА

Результаты стойкостных испытаний металлорежущего инструмента, модифицированного воздействием низкотемпературной плазмы, в производственных условиях определили целесообразность создания специального программно-математического обеспечения (ПМО), позволяющего анализировать данные о свойствах модифицированного материала с целью получения информации и создания базы знаний, необходимой для решения вопросов гарантированно повышать не только износостойкости, но и отказоустойчивости инструмента.

Разработка ПМО базируется на использовании как традиционных, так и специальных статистических методов, связанных, в частности, с идентификацией распределения данных о свойствах модифицированного инструмента [1], прежде всего физико-механических и химических.

Для идентификации распределения по статистическим данным о свойствах x строится эмпирическая кривая распределения в виде гистограммы. Для этого:

– определяется размах варьирования или широта распределения D как разность между наибольшим x_max и наименьшим x_min значениями x;

– значения x_i разбиваются на k интервалов, и определяется цена одного интервала c;

– производится подсчет частот a_j попадания значений случайной величины x в каждый интервал.

После этого последовательно определяются оценки параметров альтернативных теоретических распределений (нормального, логарифмически нормального, бета, гамма, Вейбулла, максимальных значений типа I, минимальных значений типа I), наиболее часто используемых для решения разнообразных практических задач, и по значениям плотностей их вероятностей f_j(x_с,i) производится вычисление частот a_j(x_с,i) для середин x_с каждого из k интервалов, т.е.

aj(xс, i) = fi(xс, i) × с × n, i = 1, …, k .

(3)

Для бета-распределения значения x_сi и c предварительно преобразуются по выражению и

После вычисления частот выполняется собственно процедура идентификации распределения. С этой целью для каждого распределения, включая эмпирическое, вычисляется значение количества информации I_t, характеризующее степень снятия неопределенности с массива данных x_i [1]:

(1)

где р(x_i) – вероятности появления любого из k интервалов при снятии любого из n отсчетов при условии, что одни и те же уровни могут появляться неоднократно, т.е. a(x_i) раз:

(2)

Поскольку все р(x_i) ≠ 0, функция I_t всегда определена. В тех же случаях, когда необходимо включить в рассмотрение значения р(x_i) = 0, принимается, что соответствующее произведение р(x_i)×log р(x_i) = 0.

Затем для каждого распределения вычисляется показатель, называемый коэффициентом избыточности

(4)

где I_t(x) – количество информации эмпирического распределения являющееся максимальным в силу того, максимальным количеством информации обладает сама выборка x, I_{t, j}(x) – количество информации заданного теоретического распределения. Затем в сформированном массиве k_t,j ищется минимальное значение k_min, которое будет идентифицировать распределение, имеющее наибольшую “плотность информации”, т.е. количество информации, приходящееся на один отсчет и потому снимающее неопределенность о содержащихся в выборке данных в наибольшей степени. При этом возможны следующие ситуации:

1. Коэффициент k_min < 0. Это означает, что найденное распределение не может рассматриваться в качестве модели анализируемых данных x, поскольку обладает большим количеством информации, чем сама выборка; связано это с тем, что анализируемые данные не являются однородными.

2. Коэффициент k_min > 0,05. Это означает, что среди имеющихся распределений также нет того, которое может рассматриваться в качестве модели выборки, поскольку найденное распределение не снимает неопределенности с данных x с принятой достоверностью (95%).

3. Коэффициент k_min ≤ 0,05. Это означает, что найденное распределение и есть модель анализируемой выборки, поскольку снимает неопределенность с данных x с принятой достоверностью 95%.

Алгоритм идентификации для разработки ПМО представлен на рис.1.

Если распределение данных идентифицировано, то оно используется для вычисления вероятностных характеристик анализируемых свойств модифицированного инструмента. Алгоритм вычисления представлен на рис.2.

Среднее значение вычисляется через оценки параметров распределения.

Медиана, мода и квантили определяются в процессе численного интегрирования функции плотности, поскольку интегральная функция у многих распределений аналитически не вычисляется. Шаг интегрирования Dx принимается равным 0,001.

Медиана, мода и квантили определяются в процессе численного интегрирования функции плотности, поскольку интегральная функция у многих распределений аналитически не вычисляется. С этой целью по соответствующей формуле плотности с шагом Dx, начиная с x_min, ln(x_min) для логарифмически-

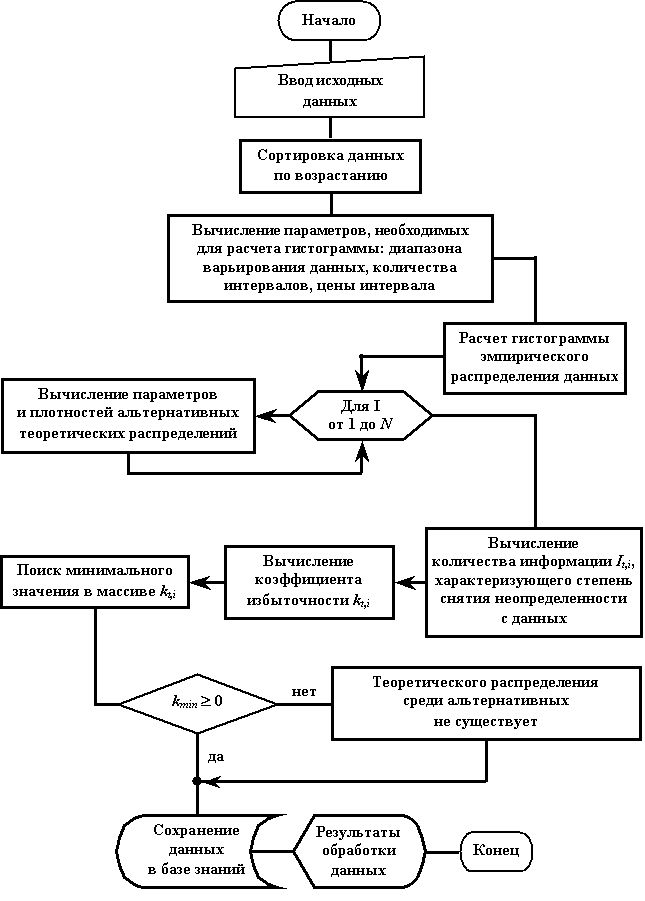
Рис.1. Алгоритм идентификации закона распределения

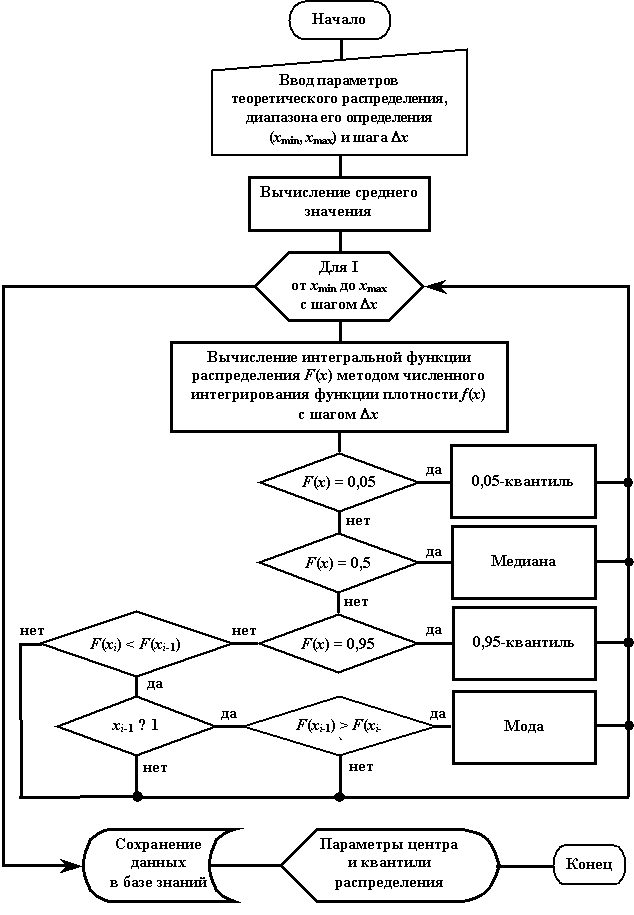
Рис.2. Алгоритм вычисления вероятностных характеристик

нормального или для бета, вычисляются f(x_i), и для определения медианы и квантилей производится их суммирование, т.е.

F(x) = Sf(xi)Dx

(5)

до тех пор, пока текущая сумма не станет равной вначале 0,05 (соответствующее значение x будет 0,05-м квантилем), затем 0,5 (соответствующее значение x будет медианой) и, наконец, 0,95 (соответствующее значение x будет 0,95-м квантилем).

В процессе численного интегрирования производится также сравнение трех последних значений f(x_i) до тех пор, пока не выполнятся условия:

(6)

Это связано с тем, что некоторые распределения (бета, гамма, Вейбулла, логарифмически нормального) при определенных условиях не имеют максимально вероятного значения. Значение x_i-1, соответствующее условиям (6), будет модой.

Для бета-распределения все найденные x преобразуются к абсолютным значениям как x = x_min + x×(x_max – x_min), для логарифмически-нормального распределения как e^x.

При создании ПМО использовался язык C#, выпущенный компанией Microsoft, как язык разработки приложений для платформы Microsoft.NET Framework. Это – простой, современный, строго типизированный объектно-ориентированный язык программирования, обеспечивающий, в то же время, поддержку и компонентно-ориентированного программирования. Разработка современных приложений все в большей степени базируется на применении программных компонентов в форме автономных и самодокументируемых функциональных модулей. Основной особенностью таких компонентов является реализация модели программирования с использованием свойств, методов, событий и атрибутов, представляющих декларативное описание компонентов, а также включение в них собственной документации. В C# представлены языковые конструкции, непосредственно поддерживающие эти понятия, что делает его близким к естественному языку для создания и применения программных компонентов.

В C# представлены функциональные возможности, позволяющие создавать надежные и устойчивые приложения. Среди них: функция сборки мусора для автоматического освобождения памяти, занимаемой неиспользуемыми объектами; функция обработки исключительных ситуаций, обеспечивающая структурированный и расширяемый подход к обнаружению и устранению ошибок; а также строго типизированная структура языка, не допускающая считывания неинициализированных переменных, выхода индекса массива за пределы допустимого диапазона или выполнения непроверенных приведений типов.

В C# применяется унифицированная система типов. Все типы C#, включая простые (например, int и double), наследуются от единственного корневого типа object. Таким образом, все типы используют набор общих операций, что обеспечивает согласованные хранение, передачу и обработку значений любого типа. Кроме того, в C# поддерживаются пользовательские ссылочные типы и типы значений, что обеспечивает динамическое размещение объектов в памяти и встроенное хранение упрощенных структур [2].

В большинстве языков программирования недостаточное внимание уделяется обеспечению совместимости и возможности дальнейшего развития программ и библиотек, в результате чего в создаваемых на таких языках программах чаще обычного возникают проблемы при переходе на новые версии зависимых библиотек. В C# реализованы следующие возможности по управлению версиями: разделение модификаторов virtual и override, применение правил разрешения перегрузки метода и поддержка явного объявления членов интерфейса.

Язык имеет статическую типизацию, поддерживает полиморфизм, перегрузку операторов (в том числе операторов явного и неявного приведения типа), делегаты, атрибуты, события, свойства, обобщенные типы и методы, итераторы, анонимные функции с поддержкой замыканий, LINQ, исключения, комментарии в формате XML. C# не поддерживает множественное наследование классов (между тем допускается множественное наследование интерфейсов). C# разрабатывался как язык программирования прикладного уровня для Common Language Runtime (CLR) и, как таковой, зависит от возможностей самой CLR. Это касается, прежде всего, системы типов C#, которая отражает Base Class Library (BCL) [3]. Присутствие или отсутствие тех или иных выразительных особенностей языка диктуется тем, может ли конкретная языковая особенность быть транслирована в соответствующие конструкции CLR. Так, с развитием CLR от версии 1.1 к 2.0 значительно обогатился и сам C#; подобного взаимодействия следует ожидать и в дальнейшем. Однако эта закономерность была нарушена с выходом C# 3.0, представляющего собой расширения языка, не опирающиеся на расширения платформы .NET. CLR предоставляет C#, как и всем другим .NET-ориентированным языкам, многие возможности, которых лишены «классические» языки программирования. Например, сборка мусора не реализована в самом C#, а производится CLR для программ, написанных на C# точно так же, как это делается для программ на VB.NET, J# и др.

Результаты практического использования ПМО позволят получить данные для оптимизации процесса плазменного воздействия с целью создания условий, в которых модифицированный слой будет наиболее эффективно замедлять процессы образования и развития дефектов на рабочей части инструмента в процессе его эксплуатации.

Литература

1. Мартынов В.В. // Статистические методы обработки экспериментальных данных / В.В. Мартынов, П.В. Мартынов. – Саратов: Сарат. гос. техн. ун-т, 2011. – 188 с.

2. Павловская Т.А. C#. Программирование на языке высокого уровня: учебник для вузов / Т.А. Павловская. – СПб.: Питер, 2007. – 432 с.

3. Шилдт Г. Полный справочник по C# / Г. Шилдт. – Вильямс, 2008. – 752 с.