Д.т.н. Кудюров Л.В., к.т.н. Гарипов Д.С.

Самарский государственный университет путей сообщения

О механизме закатывания ползуна на поверхности катания вагонного колеса

В работе [1] было принято допущение о том, что при качении смятие передней и задней кромок ползуна (рис. 1) в рабочем режиме весьма мало. Была найдена критическая скорость поезда, выше которой кромка отрывается от рельса, и ползун на мгновение «зависает» над поверхностью рельса. В следующий момент происходит удар кромки ползуна о рельс. Вследствие удара материал колеса сминается, образуется новая площадка. С периодичностью одного оборота удары повторяются задней кромкой новой площадки

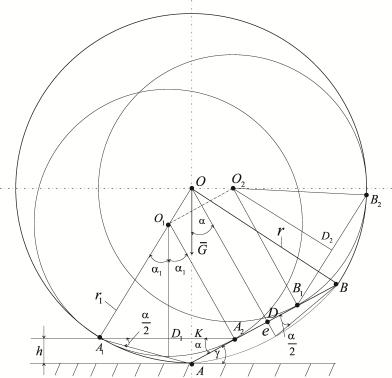
Рис. 1. Геометрия смятия кромок ползуна

до тех пор, пока ползун не исчезнет, а колесо приобретает овальную форму. Происходит «закатывание» ползуна.

При скоростях, меньших критической, в условиях отсутствия смятия кромки колесо поворачивается вокруг точки и ударяется о рельс всей поверхностью ползуна с периодичностью одного оборота. Под действием циклической ударной нагрузки происходит пластическая деформация по всей поверхности ползуна . Ползун развивается с уменьшающейся интенсивностью вследствие упрочнения материала колеса в месте контакта.

В действительности смятие кромок и ползуна при качении неизбежно, и величина меньше, чем при упомянутом выше допущении, меньше угол наклона ползуна к рельсу и, следовательно, слабее удар. Тогда разумно полагать, что при некотором, достаточно малом, значении глубины ползуна и при скорости, меньшей критической, удара не будет, а ползун «закатается» на первом же обороте. Иначе, существует граница величины , ниже которой ползун «закатывается» и при малой скорости поезда. Учитывая практическую важность информации об этой границе, оценим ее величину аналитически, исходя из того, что углы и малы так, что можно считать , , , .

Пусть под действием нагрузки поверхность катания в точке колеса сминается на величину по радиусу колеса, а в основании сминаемого объема имеем площадку радиуса (рис. 2). Но при качении смятие будет происходить

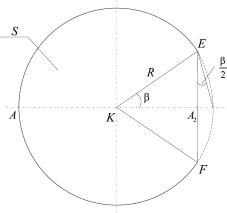
Рис. 2. Площадь основания смятого объема

по некоторой кривой. Пусть эта кривая будет дугой окружности радиуса , сопрягающей окружность колеса радиуса и прямую . Тогда - прямая линия, а параллельна вследствие того, что и перпендикулярны . Поэтому и, следовательно,

.

Из геометрических соображений (рис. 1, 2) следует:

,

,

,

,

,

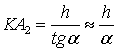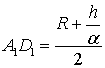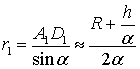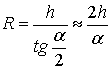, (1)

. (2)

Площадь , согласно рис. 2, равна разности площади круга радиуса и площади сегмента со стрелой, равной , то есть

.

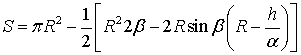Угол мал, поэтому , тогда

.

Из геометрических соображений (рис. 2) следует:

,

,

,

,

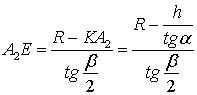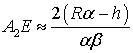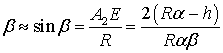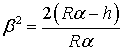откуда

.

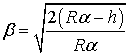С учетом этого

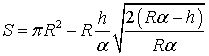. (3)

После подстановки (1) в (3) имеем

,

.

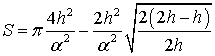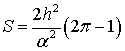С другой стороны,

,

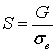где - нагрузка, Н; - предел прочности материала колеса, Па.

Следовательно,

,

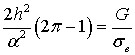откуда

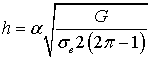. (4)

Из треугольника (рис. 1) следует

.

С другой стороны,

.

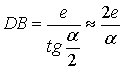Следовательно,

,

откуда

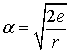. (5)

После подстановки (5) в (4) имеем

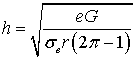. (6)

Чтобы ползун «закатывался» на первом же обороте колеса, необходимо, чтобы (рис. 1), то есть

,

или

,

,

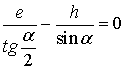откуда

. (7)

Подставляя (6) в (7), получим граничное значение в виде

.

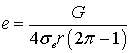Следовательно, чтобы ползун не развивался, а «закатывался» при любой скорости поезда, его глубина должна удовлетворять условию

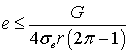. (8)

Например, пусть , , . Тогда, подставляя эти данные в формулу (8), получим

,

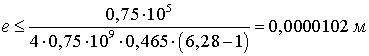или .

Литература

1. Кудюров, Л.В. Исследование динамики вагонного колеса, имеющего ползун на поверхности катания [Текст] : монография / Л.В. Кудюров, Д.С. Гарипов. - Самара : СамГУПС, 2013. - 140с.