The concept of creating analog hardware calculator as a part of hybrid architecture microcontrollers

Eurasian National University L.N. Gumilev, Astana

Ibraeva Ajgerim - Senior Researcher, Master Supervisor - Prof. SK Atanov

In this paper we consider the concept of using analog methods of information processing in these systems. Historically, analog calculations were the first and the development of technology has led to the first attempts to create an analog computer in the beginning of the 19th century. So Shannon [1] was proposed embodiment of computing differential-algebraic functions on the universal analog calculator .

One-way functions, for which the inverse transformation exists and is uniquely, but has a high computational complexity are more commonly used for the construction of modern cryptographic information protection systems. This so-called computationally irreversible functions [2]. For example, a one-way function on the basis of the calculation of discrete logarithms in a group of algebraic Galois field. The safety of using one-way function ElGamal with a secret passage is also based on the computational complexity of the discrete logarithm problem in the algebraic field of high dimension [2].

As an example of a one-way function y = f (x) we consider the well-known function of the discrete exponentiation: y = ах (mod p), where x - an integer from 1 to p - 1, inclusive, and the calculations are done modulo p, where p - a very large prime number; a - an integer (1 <a <p). Recall that a prime number is an integer that is not divisible by any number other than itself and one. The function у=ах(mod p) is calculated relatively simply, and its inverse function x=logyp is computationally difficult for almost all (1 <y <p), provided that p is not only large, but also (p - 1) has a large prime factor (better if it is another prime numbers multiplied by 2). In this regard, such a problem is called the problem of finding the discrete logarithm or the discrete logarithm problem.

The discrete logarithm problem is that for as much as a well-known, а, р, у  need to find an integer x. However, the algorithm for computing discrete logarithms in a reasonable time is not yet found. Therefore modular exponent is considered one-way function.

According to current estimates of number theory with integers a≈2664 and p≈2664 solving the discrete logarithm problem will require about 1026 operations, which has 103 times the computational complexity than the problem of factoring. With increasing numbers of length difference in the estimates of the complexity of problems increases.

Traditionally, these problems are solved with signal processors with varying success. Architecture of signal processors compared to general purpose microprocessors has some features associated with the desire to speed up common tasks of digital signal processing such as digital filtering, Fourier transform, the search for signals and so on [11]. Mathematically, these problems can be reduced to the element-wise multiplication of elements multicomponent vectors of real numbers, then summing the products (for example, in digital filtering the output signal of the filter with finite impulse response is equal to the sum of the products of filter coefficients in the vector of signal samples, similar calculations are made in finding the maxima of the correlation functions and autocorrelation signal samples). Therefore, signal processors are optimized for speed to perform such operations and is focused primarily on multiple execution of multiplication. All this eventually requires high speed and a multi-core processor that leads to high product cost and high power consumption.

An alternative way to increase the speed of calculation is the use of PLD - programmable logic device. Construction of high-speed multipliers, and an example of implementation of DSP algorithms on PLD sufficiently discussed in detail in [6]. Implementation of multiplication hardware methods has always been a challenge in the development of high-performance solvers. Thus, a full parallel multiplier 4 * 4 requires for its implementation 12 adders. With an increase in the bit matrix of the single-digit adders significantly expands and simultaneously increases critical path and implementation of the multiplier is becoming irrational.

Implementation of mathematical functions on the PLD requires the creation of large combinational circuits, such as multipliers and dividers, resulting in the use of logical resources unnecessarily increasing. For example, multiplication is, in fact, an iterative addition, but, as a rule, the PLD synthesis tools implement this operation using a complex combinational logic. It should be noted that the division operation in such instruments to realize more complicated. Thus, the controversial winner in computing speed on PLD, we obtain a significant rise in production and lose flexibility reconfiguration, as the architecture of PLD is formed each time for a specific task.

The basic concept of the use of analog computation in digital systems is the integration of the microcontrollers and digital hardware and analog calculator. For this purpose, computer architecture is complemented with module analog microcontrollers. Figure 2 shows the architecture of the proposed options for calculating with integration of the system bus, which allows a brief explanation of the concept of digital-to-analog computing.

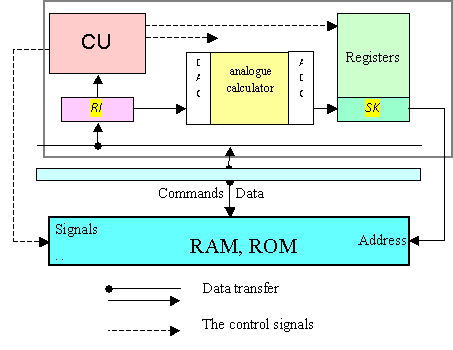
Figure 2 - Architecture of the hybrid calculator

Computer supplemented with analogue block on the basis of an analog computer with an analog-to-digital and digital-to-analog converters. This architecture provides the mathematical operations in hardware analog form and then converts the results into digital form.

After performing mathematical operations results are converted by the ADC into a digital format and supplied to the data bus. Contacting an analog calculator through specialized registers allows preserving the traditional architecture and management system that will ensure compatibility with existing digital devices and software.

So, for example a solution of the differential equation of the form:

accepts a hardware form (Figure 3) with the use of modules integration

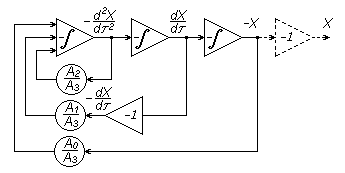
Figure 3 - The hardware solution of differential equations

Specifying the correct initial conditions provide an unambiguous and stable analog hardware solution for subsequent digital interpretation. Development of software applications for analog blocks will allow access them from traditional programming languages by plugging the appropriate library extensions.

The main advantage of the proposed concept of the use of analog computation in digital systems:

- parallel hardware processing of digital and analog signals, accelerating cryptographic processing information;

- a wide range of commands for hardware signal processing (trigonometric and exponential functions, filtering, Fourier ,Walsh, Hartley transforms, etc.) that reduces the software part and accelerating cryptocalculating;

- hardware and software compatibility with existing computer systems.

All this will allow for cryptographic processing signals on the basis of hardware measurements without the need for software implementation and execute them in a single cycle of the analog calculator. This solution allows to accelerate not only the cryptographic operations, but also the calculation of special signal processing functions as trigonometric, exponential operations, as well as to solve differential and nonlinear equations, depending on the composition of the modules of the analog calculator. This architecture is not free from drawbacks, which must be attributed primarily low accuracy of the calculation, which can be overcome by software and the use of precision operational amplifiers.

1 Shannon, C. A mathematical theory of the differential analyzer / Shannon // work on information theory and cybernetics / Translated from English. - Moscow: Mir, 1963 - 709-728 p.

2 Theory of telecommunications: a tutorial / K.K. Vassiliev, V.A. Glushkov, A.V. Dormidontov, A.G. Nesterenko, under the total ed. K.K. Vasiliev. - Ulyanovsk Ulyanovsk State Technical University, 2008 - 452 p.