УДК 631.316.022.4

К.т.н., доцент Пугач А.Н., к.т.н., доцент Колбасин В.А., бакалавр Литвинцева Ю.О., магистр Носенко А.В., магистр Лисняк В.С.

Днепропетровский государственный аграрно-экономический университет

Проектирование развертки торсовой поверхности культиваторной лапы

Постановка проблемы. Разработка конструкции почвообрабатывающих рабочих органов обладающих заданными параметрами является важной задачей, так как позволяет максимально улучшить технологический процесс почвообработки. В этой связи разработка геометрических моделей поверхностей конкретных рабочих органов позволяет при проектировании учесть все необходимые факторы.

Анализ исследований. Многочисленными исследованиями установлено, что при проектировании поверхностей почвообрабатывающих рабочих органов наиболее пригодны торсовые поверхности ввиду их высоких технологических свойств, при изготовлении и взаимодействии с почвой [1].

Торсовые поверхности образуются движением в пространстве прямой линии, имеющей   точку касания с пространственной кривой, которая называется ребром возврата и налагает на существование поверхности определенные требования. Торсовые поверхности можно образовать различными способами, в том числе и уравнением непрерывного каркаса образующих [2]. В этом случае  положение образующих удобно задавать функцией некоторого параметра.

Одним из способов образования поверхности является способ, основанный на  введении коэффициента, который является аналогом гауссовой кривизны [5]. Обладая большой  общностью, этот способ нуждается в доработке применительно к культиваторным лапам.

Цель исследований. Разработка геометрической модели поверхности культиваторной лапы, позволяющей вести  проектирование в большом диапазоне параметров применительно к конкретным условиям.

Основной материал исследований. Поверхность культиваторной лапы образуется движением в пространстве прямой линии g, которая называется образующей [3,2].

Согласно рисунку 1 запишем положение  проекции образующей g следующим образом:

                                                       ,

                                                       ,                                                    (1)

где k,l,m,n – функции некоторого параметра  u.

Запишем уравнение  образующей (1) в функции координаты :

                                                        ,

                                                   ,                                                (2)

где k и mk – угловые  координаты  расположения прямой на плоскостях проекций;

     l и ml + n – свободные  члены уравнений образующей.

Для  обеспечения торсовости поверхности культиваторной лапы на величины k, mk, l и ml + n налагается дифференциальное условие [4]:

                                                             

где штрихи обозначают первую производную по  параметру u.

Дифференцируя, имеем:

                                                          

Проведя преобразование, приходим к следующему дифференциальному уравнению положения образующей g:

                                            ,                                                (3)

которое можно разрешить относительно одного из угловых коэффициентов.

Так, если задан угловой коэффициент k, то недостающий угловой коэффициент определиться следующим дифференциальным уравнением, относительно m:

                                                           ,                                                     (4)

а если задан угловой коэффициент m, то уравнение, относительно неизвестного k примет вид:

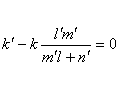                                                                                                           (5)

В каждом положении образующая g имеет общую точку Е с направляющей кривой (L). Для культиваторной лапы направляющая кривая (L), представляет собой плоскую линию, являясь контуром лезвия. Ее уравнение будет иметь вид:                              , ,

где  параметр u имеет тот же смысл, что и b (1). 

 

 

                                         

 

 

 

 

 

 

 

 

 

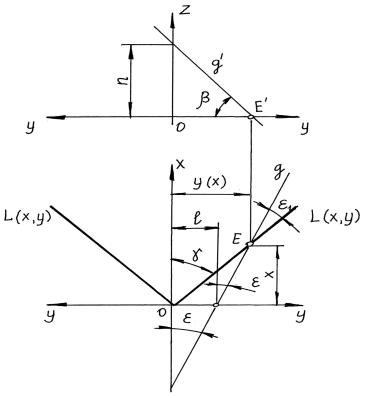
Рис 1. Схема образования торсовой поверхности культиваторной лапы

Для удобства примем в качестве параметра u координату x, что дает следующее уравнение направляющей (L): .

Выразим величины, входящие  в дифференциальное уравнение  (4) и (5) через координаты точки Е.

Из геометрических соображений угловые коэффициенты  равны:

                                                            ,

                                                           .

В свою очередь свободные члены из треугольников FME и OPE´ равны:

                                                       ,

                                                         .

Подставляя полученные значения  параметров в (4) и (5) соответственно приходим к дифференциальному уравнению  относительно угла наклона проекции образующей на плоскости 0yz:

                                ,

и  относительно угла наклона проекции образующей на плоскости 0xy:        

Из приведенных уравнений  видно, что заданные функции  в качестве неизвестной проще, чем задание функции , так как в первом случае получаем линейное однородное дифференциальное уравнение.

Если в качестве направляющей (L) принять прямую линию с уравнением

                                                          ,

а функцию наклона горизонтальных проекции образующих , то дифференциальное уравнение положения образующих будет выглядеть так:

                                          (6)

В самом простом  случае функция угла наклона горизонтальной проекции образующих равна постоянной величине, что означает постоянный угол наклона   вдоль оси ОХ. Так как , то решение дифференциального уравнения (6) предстанет в следующем виде:

                                                            .

Интегрирование этого уравнения дает  постоянную величину угла наклона образующей на плоскости OYZ,  что в свою очередь означает, вырождение торсовой поверхности в плоскость.

Рассмотрим простой случай, когда функция угла наклона образующих задана следующим образом:

                                                          .

Подставляя в дифференциальное уравнение положение образующих (6) функцию будем иметь:

                               .

Проведя преобразование, получим следующее дифференциальное уравнение:

                                           ,

общее решение которого имеет вид:

                                                              ,

          где:       

Постоянная интегрирования находится следующим образом:

                                                             ,

где и  – начальные значения угла наклона проекции образующей и начальное значение координаты х .

Выражение  интегрируется методом неопределенных коэффициентов. Разложив знаменатель на множители, получим:

,

где  –  корни полинома;

     – коэффициенты,  которые определяются из системы уравнений.

Если в числителе выражения будет полином то уравнение (6) всегда интегрируется.

Поверхность будет существовать и в тех случаях, когда уравнение (6) будет решаться численными методами. В этом случае для перехода от дискретного каркаса образующих к непрерывному, необходимо выполнить операцию  интерполирования между соседними образующими.

Выводы. Предложена геометрическая модель поверхности культиваторной лапы, позволяющая изменением одной функции положения образующей получить различные поверхности применительно к конкретным условиям работы почвообрабатывающего орудия.

Список литературы

1. Бурченко П.Н. Механико-технологические основы почвообрабатывающих машин нового поколения. – М.: ВИМ. 2002. – 211 с.

2. Кривошапко С.Н. Торсовые поверхности и оболочки: Справочник. – М.: Из – во УДН,  – 1991. – 287 с.

3. Рыжов Н.Н. Алгоритмизация вывода уравнений линейчатых поверхностей с учетом наперед заданных условий // Прикладная геометрия и инженерная графика. – Киев, – 1972.-Вып.4. – С.3-8.

4. Рыжов Н.М., Алимов Р.У. К вопросу конструирования торсов по наперед заданным условиям // Прикладная геометрия и инженерная графика. – К. – 1979. – Вып. 27. – С. 15 – 17.

5. Тищенко С.С., Волик Б.А. Обобщенная геометрическая модель адаптивной поверхности  рабочего органа почвообрабатывающей машины // Праці Таврійської державної агротехнічної академії. – Мелітополь. – 2001. – Том. 18. – Вип.2. – С. 39 – 44.

Annotation

Geometric model of cultivating claw on the base of trunk surface, which allows to build a working surface with the help of a given law of forming distribution is worked out.