MATHEMATICS / 4. Applied Mathematics

Iskakova A., Estavletova Sh.

L.N. Gumilev Eurasian National University, Astana, Kazakhstan

About unbiased estimators for discrete distribution of sums of random variables

Introduction. As was noted in [1], issues of legal violations by minors in Central Asia, particularly in Kazakhstan, the last few years strongly become aggravated. For example, on the basis of statistical data, which were provided by the Agency of the Republic of Kazakhstan on Statistics (see [2]), in Table 1 we can see the dynamics of the number of crimes by minors in the Rudny town (Kostanay region, Kazakhstan). Note that the population of the Rudny town is about 128 thousand.

Table 1.

Dynamics of the number of crimes by minors in the Rudny town (Kostanay region, Kazakhstan).

Year	2007	2008	2009	2010	2011	2012	2013	2014	2015
The number of crimes by minors	60	21	17	21	1	23	22	10	9

Obviously, the dynamics of minors delinquency depends from the following factors (see[3-7]): economic (price increases, low income of the general population, the demographic structure of the population), social (the sharp deterioration in the psychological climate in families of the unemployed, alienated parents from the responsibility for the education of children, forced to search for minors own sources of income devaluation of family values, the institution of marriage as the basis of a normal life of people in the community) and legal factors (changes in the criminal law, expanding or narrowing the scope of a criminal offense and, changing the classification and qualification of crimes and crime detection).

Thus, the probability values of number of crime among minors amounts depend on the probability of the impact of relevant factors. And the study of the probability of the number of crimes that are presented as the sum of the relevant factors, the most realistic, than the study of the probability of the number of crimes without concretizing these factors. Of course of the theory of probability it is clear that these factors have a polynomial distribution (see [8]).

Any crime committed minors, is a consequence of the influence of group of factors. Let’s that the crime x is influenced N factors with some degree of the actions. Define for each factor the one of the possible values l₁, l₂, ..., l_n with the corresponding values of the probabilities p₁, … , p_n , and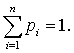

.Let’s that the crime u is influenced k factors. And the factor l₁ influenced the crime х the r₁ times, the factor l₂ influenced the crime х the r₂ times and so forth the factor l_n influenced the crime х the r_n times. It’s obvious that.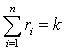

We have the following from course of combinatorics (see. [15]). The number of of all possible influences k factors, in which the factor l₁ influenced the crime u the r₁ times, the factor l₂ influenced the crime х the r₂ times and so forth the factor l_n influenced the crime х the r_n times, is defined as

.

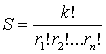The probability that the crime х was dependent on k factors, in which the factor l₁ influenced the crime х the r₁ times, the factor l₂ influenced the crime х the r₂ times and so forth the factor l_n influenced the crime х the r_n times, is

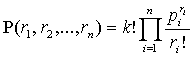, (1)

where volues p₁, … , p_n are probabilities of factors l₁, l₂, ..., l_n influenced the crime х. The formula (1) is the polynomial distribution of probability (see [15]).

Consider the dynamics of crimes of minors in the Rudny town (Kostanay region, Kazakhstan) presented in Table 1.

Let us assume that the economic factor can affect the state of crime among adolescents with probability 0.7, the 2nd factor with 0.2, 3rd with 0.1. Proposed partitions of the factors affecting the dynamics of juvenile delinquency in the Rudnyy town (Kostanay region, Kazakhstan) are presented in Table 2.

Table 2.

Proposed partitions of the factors affecting the dynamics of juvenile delinquency in the Rudnyy town (Kostanay region, Kazakhstan)

Year		2007	2008	2009	2010	2011	2012	2013	2014	2015
The number of crimes by minors		60	21	17	21	1	23	22	10	9
Partition 1	Factor 1	30	20	15	15	1	10	20	5	5
	Factor 2	20	1	1	6	0	10	1	3	3
	Factor 3	10	0	1	5	0	3	1	2	1
Partition 2	Factor 1	45	15	16	18	0	15	20	5	5
	Factor 2	10	6	1	3	1	5	1	4	4
	Factor 3	5	0	0	0	0	3	1	1	0

Partition Configuration of factors there is a significant set. So for the first embodiment of partitions factors for 2015 have

.

Let’s we have the crime u, which is the sum k factors. In other words

.

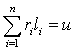Last formula is formula of partitions of u on parts l₁, l₂, ..., l_n with the number of partitions n.

The probability that the sum of k factors influence the crime x is equal to u, is defined by the formula

.

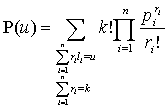Thus, for datas of Table 2 for 2015 we have

Discussion & Conclusion. Presented probabilistic model of surveillance reveals the problem need detailed approach to the study of factors affecting the dynamics of juvenile delinquency.

References:

1. Bimbetov A. B. Ultimate Fact Distinctions in Criminal Cases Involving Juveniles in the Russian Federation and the Republic of Kazakhstan //Middle-East Journal of Scientific Research. – 2013. – Т. 13. – №. 5. – С. 636-639.

2. Mersky J. P., Topitzes J., Reynolds A. J. Unsafe at any age linking childhood and adolescent maltreatment to delinquency and crime //Journal of research in crime and delinquency. – 2012. – Т. 49. – №. 2. – С. 295-318.

3. Hinduja S., Patchin J. W. Social influences on cyberbullying behaviors among middle and high school students //Journal of youth and adolescence. – 2013. – Т. 42. – №. 5. – С. 711-722.

4. Belkin M., Sinha K. Polynomial learning of distribution families //SIAM Journal on Computing. – 2015. – Т. 44. – №. 4. – С. 889-911.

5. Cole B., Chipaca A. Juvenile delinquency in Angola //Criminology and Criminal Justice. – 2014. – Т. 14. – №. 1. – С. 61-76.

6. Veltri C. O. C. et al. Distinguishing Personality Psychopathology Five (PSY–5) characteristics associated with violent and nonviolent juvenile delinquency //Journal of personality assessment. – 2014. – Т. 96. – №. 2. – С. 158-165.

7. Coleman J. S. et al. Introduction to mathematical sociology //London Free Press Glencoe. – 1964.

8. Anderberg M. R. Cluster analysis for applications: probability and mathematical statistics: a series of monographs and textbooks. – Academic press, 2014. – Т. 19.

9. Fine T. L. Theories of probability: An examination of foundations. – Academic Press, 2014.

10. Nelson R. Probability, stochastic processes, and queueing theory: the mathematics of computer performance modeling. – Springer Science & Business Media, 2013.

11. Percus J. K. Combinatorial methods. – Springer Science & Business Media, 2012. – Т. 4.

12. Panaretos J., Xekalaki E. On generalized binomial and multinomial distributions and their relation to generalized Poisson distributions. // Ann. Inst. Math. 1986.V.38.Part A. P. 223 – 231.

13. Ayman I. Construction of the most suitable unbiased estimate distortions of radiation processes from remote sensing data //Journal of Physics: Conference Series. – IOP Publishing, 2014. – Т. 490. – №. 1. – С. 012113.

14. Iskakova A., Ibragimov B. A method for determining an unbiased estimate // Nauka i Studia. – Przemyśl: Nauka i studia. - NR 7 (52), 2012. –P. 86-91.