Евразийский национальный университет имени Л.Н. Гумилева

Вероятностное представление динамики преступности среди несовершеннолетних

1. Введение. Одним из индикаторов, характеризующих социальное здоровье общества, является преступность несовершеннолетних. Состояние преступности, как правило, достаточно точно отражает степень благополучия социальной ситуации.

Очевидно, что на динамику преступности среди подростков влияют следующие факторы: экономические (рост цен, низкий уровень доходов основной массы населения, демографическая структура населения), социальные (резкое ухудшение психологического климата в семьях безработных, отчуждение родителей от обязанности по воспитанию детей, вынужденный поиск несовершеннолетними собственных источников дохода девальвация семейных ценностей, института брака как основы нормальной жизни людей в обществе) и юридические факторы(изменения уголовного законодательства, расширяющие либо сужающие сферу преступного и наказуемого, меняющие классификацию и квалификацию преступлений, а также раскрываемость преступлений).

Вероятностное изучение всех количественных показателей преступлений опирается на вероятность влияний соответствующих факторов. Из курса теории вероятности очевидно, что данные факторы можно рассмотреть как полиномиально распределенные. Однако, распределение вероятности суммы полиномиально распределенных случайных величин и его применение в социальных исследованиях в научной литературе имеется в [1, с. 79], [2, с. 012113], [3, с. 86].

Однако, если расматривать ситуации, при которых на исследуеммые события были наложенны неизвестные явления, иными словами неявные предпосылки, то остается много нерешенных проблем.

2. Построение вероятностной модели событий зависимых от факторов. Любое преступление, совершенное несовершенолетними, является последствием влияния группы факторов. Допустим, что на преступление x влияет N факторов с некоторой степенью действия. Определим каждый фактор одним из возможных чисел l₁, l₂, ..., l_n с соотвествующими значениями вероятностями p₁, … , p_n, и

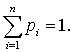
Пусть на преступление u могут влиять k факторов с возможными повторениями. Причем фактор l₁ повлиял на преступление х r₁ раз, фактор l₂ повлиял на преступление х r₂ раз и так далее фактор l_n повлиял на преступление х r_n раз. Очевидно, что

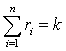Теорема 1. Количество всевозможных влияний k факторов с повторениями, при которых фактор l₁ повлиял на преступление u r₁ раз, фактор l₂ повлиял на преступление х r₂ раз и так далее фактор l_n повлиял на преступление х r_n раз, определяется как

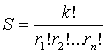Доказательство очевидно из курса комбинаторики (см. [4, с. 19]).

Теорема 2. Вероятность того, что на преступление х повлияли k факторов с повторениями, при которых фактор l₁ повлиял на преступление х r₁ раз, фактор l₂ повлиял на преступление х r₂ раз и так далее фактор l_n повлиял на преступление х r_n раз, есть

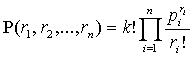, (1)

где значения p₁, … , p_nопределяют вероятности (или частности) влияния фактора с соответствующим числом l₁, l₂, ..., l_n на преступление х.

Доказательство. Очевидно, что в данном случае мы имеем полиномиальное распределение вероятностей, которая имеет форму (1) (см. [5, c.223])

Теорема доказана.

Пример 1. При обзоре анализа динамики преступности среди несовершеннолетних по городу Рудный (Кустанайская область, Казахстан) имеем данные, представленные в таблице 1.

Таблица 1.

Динамика преступности среди несовершеннолетних по г. Рудный (Кустанайская область, Казахстан)

Год	2007	2008	2009	2010	2011	2012	2013	2014	2015
Количество преступлений	60	21	17	21	1	23	22	10	9

Допустим, что экономический фактор может повлиять на состояние преступности среди подростков с вероятностью 0,7, 2-й фактор 0,2, 3-й – 0,1. Предположительные варианты разбиений факторов, влияющих на динамику преступности среди несовершеннолетних по г. Рудный (Кустанайская область, Казахстан) представлены в таблице 2.

Таблица 2.

Предположительные варианты разбиений факторов, влияющих на динамику преступности среди несовершеннолетних по г. Рудный (Кустанайская область, Казахстан)

Год		2007	2008	2009	2010	2011	2012	2013	2014	2015
Количество преступлений		60	21	17	21	1	23	22	10	9
Вариант 1	Фактор 1	30	20	15	15	1	10	20	5	5
	Фактор 2	20	1	1	6	0	10	1	3	3
	Фактор 3	10	0	1	5	0	3	1	2	1
Вариант 2	Фактор 1	45	15	16	18	0	15	20	5	5
	Фактор 2	10	6	1	3	1	5	1	4	4
	Фактор 3	5	0	0	0	0	3	1	1	0

Вариантов разбиений факторов существует значительное множество. Так для первого варианта разбиений факторов для 2015 года имеем

3. Вероятностное распределение суммы факторов влияющих на преступление. Допустим, имеем некоторое преступление со значением u, представляемое сумму k значений факторов, повлияющих на преступление х. То есть

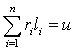. (2)

Последняя формулая явлется формулой разбиения числа u на части l₁, l₂, ..., l_nчислом разбиений n.

Теорема 3. Вероятность того, что сумма чисел на k повлияющих факторах с повторениями на преступление x равна u, определяется по формуле

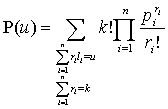Доказательство. Разумеется, что, если имеет место разбиения u на l₁,…, l_d, то система уравнений

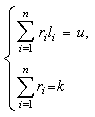
имеет один или более решений. Вероятность каждого разбиения u на l₁,…, l_d, определяется теоремой 3. Таким образом, пришли к доказательству теоремы.

Теорема доказана.

Пример 2. Из примера 1 допустим возможны только два варианта разбиений факторов, которые представлены в таблице 2. Так для первого для 2015 года имеем

Литература:

1. Искакова А. С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии //Сибирский журнал индустриальной математики. – 2002. – Т. 5. – №. 1. – С. 79-84.

2. Ayman I. Construction of the most suitable unbiased estimate distortions of radiation processes from remote sensing data //Journal of Physics: Conference Series. – IOP Publishing, 2014. – Т. 490. – №. 1. – С. 012113.

3. Iskakova A., Ibragimov B. A method for determining an unbiased estimate // Nauka i Studia. – Przemyśl: Nauka i studia. - NR 7 (52), 2012. –P. 86-91.

4. Сачков В. Н. Комбинаторные методы дискретной математики. – Издательство" Наука", Главная редакция физико-математической литературы, 1977.

5. Panaretos J., Xekalaki E. On generalized binomial and multinomial distributions and their relation to generalized Poisson distributions. // Ann. Inst. Math. 1986.V.38.Part A. P. 223 – 231.