Математика /1.Дифференциальные и интегральные уравнения

к.ф.м.н, доцент І.І. Дрінь, к.ф.м.н. Н.М. Шевчук

Чернівецький торговельно-економічний інститут КНТЕУ, Чернівецький національний університет імені Юрія Федьковича, Україна

Властивість локалізації формальних рядів Ерміта

Нехай - функції Ерміта, які утворюють ортонормований базис в ,

- фіксовані параметри. Простори введені в [1]. Якщо і то кожна функція з цього простору допускає аналітичне продовження у всю комплексну площину і задовольняє нерівність

Функції з простору допускають аналітичне продовження в деяку смугу комплексної площини (залежну від функції). Якщо то простір містить вже фінітні функції.

Символом позначатимемо простір, топологічно спряжений до , елементи цього простору (лінійні неперервні функціонали, задані на ) називатимемо узагальненими функціями. Зазначимо, що функції Ерміта , є елементами простору . У зв’язку з цим формальним рядом Ерміта узагальненої функції назвемо ряд 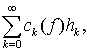де - коефіцієнти Ерміта (тут позначає дію функціоналу на основну функцію). Із результатів, отриманих в [2] випливає, що простір можна розуміти як простір формальних рядів Ерміта вказаного вигляду, тобто кожну узагальнену функцію можна ототожнити з її формальним рядом Ерміта, при цьому послідовність частинних сум такого ряду збігається до у просторі (тобто, в слабкому розумінні).

Перетворенням типу Гаусса-Вейєрштрасса ряду Ерміта узагальненої функції називається перетворення вигляду

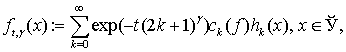(1)

де - фіксовані параметри.

Теорема 1. Правильними є наступні твердження.

а) Якщо , то ряд (1) збігається при кожному рівномірно по ;

при кожному і .

б) Для функції справедливе зображення

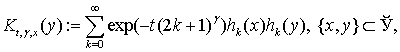
при кожному .

в) при у просторі .

Для класичних рядів Ерміта має місце аналог відомого принципу локалізації Рімана для тригонометричних рядів [3]: якщо функції збігаються на інтервалі , то на будь-якому відрізку різниця їхнії рядів Ерміта рівномірно збігається до нуля. У класі розподілів цей принцип вже не виконується. Наприклад, ряд Ерміта -функції Дірака має вигляд

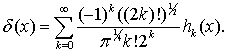(2)

Нагадаємо, що ряд (2) збігається до -функції у просторі , тобто в слабкому розумінні. Використавши формулу Дарбу та асимптотичну формулу для ортонормованих многочленів Ерміта [3] знаходимо, що

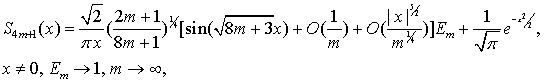
де - відповідна частинна сума ряду (2).

- функція Дірака дорівнює нулеві на довільному проміжку, який не містить точку , але її ряд Ерміта, як це випливає з останнього співвідношення, не збігається рівномірно до нуля на довільному такому проміжку. Однак, у багатьох задачах математичної фізики, де користуються зображенням функцій у виглядів рядів, більш природним є виконання принципу локалізації не для самих рядів, а для рядів, просумованих деяким методом. Так, наприклад, принцип локалізації для тригонометричного ряду Фур’є - періодичної функції , просумованого методом Абеля-Пуассона, еквівалентний принципу локалізації для розв’язку задачі Діріхле для рівняння Лапласа в одиничному крузі з граничною функцією , заданою на колі: якщо на деякій відкритій частині кола збігається з неперервною функцією, то при наближені до межі круга по недотичних напрямах розв’язок задачі Діріхле збігається до рівномірно на кожній замкненій частині цієї ділянки кола. Виявляється, якщо ряд Ерміта узагальненої функції просумувати методом типу Гаусса-Вейєрштрасса, то принцип локалізації виконується вже у досить широкому класі узагальнених функцій нескінченного порядку. Отже, у даному випадку має місце локальне покращення збіжності.

Теорема 2 (принцип локалізації). Якщо і на інтервалі (тобто для довільної функції , носій якої міститься в ), то при рівномірно відносно на довільному відрізку .

Наслідок. Якщо узагальнена функція збігається на інтервалі з неперервною функцією , то при рівномірно відносно на довільному відрізку .

Література

1. Гельфанд И.М. Пространства основних и обобщенных функцій / И.М.Гельфанд, Г.Е Шилов.-М.: Физматгиз, 1958.-307с.

2. Горбачук В.И. Граничные задачи для диференциально-операторных уравнений / В.И Горбачук, М.Л. Гобачук.-Киев: Наук. думка, 1984.-284с.

3. Суетин П.К. Классические ортогональне многочлены / П.К. Суетин.-М.: Наука, 1976.-328с.