Математика/ 1.Дифференциальные и интегральные уравне­ния.

К.ф.-м. н. Ысмагул Р.С.

Костанайский государственный университет им. А.Байтурсынова, Казахстан

     Метод укорочения для некоторых систем дифференциальных уравнений в частных производных

 

       При исследовании нелинейных уравнений в частных производных с помощью метода укорочения [1] возникает задача, связанная с решением счетной системы обыкновенных дифференциальных уравнений [1-2]. В настоящей статье рассматривается аналогичная задача об укорочении счетной системы дифференциальных уравнений, к которой приходим, применяя при изучении  некоторых систем  метод укорочения.

Рассмотрим систему интегро-дифференциальных уравнений вида

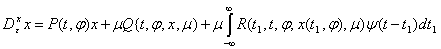     ,                     (1)

где x,Q,R– n векторы-столбцы; P(t,φ) – матрица размерности n×n,  φ = ( φ1, …, φт, …) – счетномерный вектор, , >0 – малые параметры. - дифференциальный оператор вида , где . Положим, что    ,

,

  где ,-положительные  постоянные.

Пусть n-мерное вектор функция определена и непрерывна в области  ,  где  счетно-мерный вектор с нормой  .

Введем некоторый класс n- мерных вектор-функций от счетномерного вектора , где основную роль играет усиленное условие Липщица введенное К.П.Персидским, удовлетворяющих условиям  , почти многопериодических  по    с -вектор –почти периодом , где при .

Пусть .Рассмотрим  дифференциальный оператор

.

Для сокращения записи введем .Заметим что коэффициентами  усиленного условия Липшица  для  вектор-функции   являются .

   Пусть  - характеристическая функция оператора , которая удовлетворяет интегральному уравнению

.

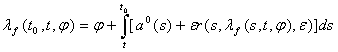Для характеристической функции имеют место оценки, аналогичные соотношениям вида I(a-b) и 10-90 [1].

Рассмотрим линеаризованное уравнение: .               (2)

Пусть -матрица типа Грина для уравнения (2) .Будем считать, что выполняется группа оценок , аналогичным оценкам  II(a-b) [1].

Рассмотрим оператор Т, отображающий каждую вектор-функцию  в вектор-функцию

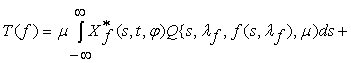
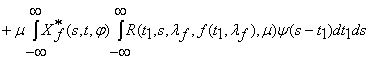
Пусть,

где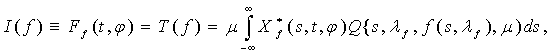  

которое известно из [2]. Будем изучать

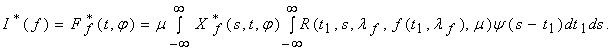
Полагая теперь , можно записать . Из оценок III(a-d) [2] следует, что существует  такое число , для которого при всех  выполняются соотношения:

1)   ,

2)   ,         

3)   ,

4)   .

Тем самым приходим к утверждению следующей теоремы .

Теорема. Если уравнение (2) некритическое относительно класса  и выполнены условия ,  для уравнения (1), то для всех значений ,  уравнение (1) имеет единственное почти многопериодическое решение из класса , сходящиеся при  в нулевой вектор.

 

Литература

                1.Умбетжанов Д.У. Почти периодические решения эволюционных  урав-

       нений.  Алма-ата, Наука, 1990, 188 с.

 2. Исмагулова Р.С. О применении метода укорочения к построению почти многопериодического решения одной системы интегродифференциальных уравнений частных производных // Алма-Ата, 1987, 25 с. Деп. в ВИНИТИ 3.07.87.№5474-В.87 Деп.