Метод
наименьших квадратов и числовые оценки микронеровности края наноструктур
Авторы: Никитин А.В., Руденко А.Ю., Сафонов П. А.
(Институт Искусств и Информационных Технологий, Москва)
Неровность края элементов топологического
рисунка современных интегральных схем становится все более важной
характеристикой при оценках надежности
создаваемых устройств и уровня технологии
производства в целом. Есть основания считать, что существует корреляция между неровностью
края, т.е. изрезанностью периметров
планарных транзисторов – основы любых современных интегральных схем – и частотой отказов (сбоев) в работе соответствующей аппаратуры. В
настоящее время неровность края большинства ответственных изделий
микроэлектроники регламентируется соответствующими руководящими техническими
материалами. Требования к уровню допустимых значений неровности края
микроэлектронных изделий включены в перечень важнейших характеристик разрабатываемых технологий и новых поколений интегральных
схем. [1]
Эту характеристику принято количественно
оценивать как среднеквадратическое отклонение (СКО) фактического положения края
элемента на разных участках (строках) его изображения от идеализированной «опорной» мысленной прямой линии.
В
современной электронной промышленности для измерений размеров элементов
интегральных схем (полосок, линий), так
же, как и для оценок неровности края (Line Edge Roughness – LER) используются сканирующие электронные микроскопы Scanning Electron Microscopes – SEM. При этом осуществляется т.н. цифровое (дискретное) перемещение электронного
зонда по строке, а изображение объекта представляет собой совокупность таких
строк. Такая организация сканирования оказывается удобной как для измерения
размеров, так и для оценок LER. Поэтому
оценки величины LER производятся обычно в ходе специальной дополнительной компьютерной
обработки SEM-изображений, фиксируемых в
ходе вычислений размеров топологических элементов – без необходимости повторной
записи SEM-изображений.
Если
опорная прямая линия задана, например, в форме «с угловым коэффициентом», то задача
количественной оценки неровности края обычно сводится к локализации фактических
положений краев элемента на различных строках его увеличенного изображения, построчному вычислению индивидуальных
отклонений найденных координат края от идеализированной «опорной» прямой линии и
последующим расчетом разброса: дисперсии, среднеквадратичного отклонения СКО (Standard Deviation).
Таким
образом, первой задачей на этом пути оказывается отыскание указанной «опорной»
прямой линии. Такая задача решается наиболее удобно с использования известного метода наименьших квадратов – МНК [2,3].
Для начала процедур МНК необходимо выполнить 3 условия:
1. Иметь в наличии массив фактических,
экспериментальных значений координат края на разных строках изображения – Хэ(i); (здесь i
– номер строки);
2. Выбрать модель искомой «опорной» прямой – т.е. вид
уравнения опорной линии. В данном случае моделью может стать уравнение
Хм(i)=a(i)+b. (1)
Здесь Хм(i) – х –координата края структуры, вычисляемая по
модели (1)
3. Выбрать начальное приближение модели, т. е.
начальные значения коэффициентов модели – а и b: a0 и b0.
Коэффициенты a0 и b0 желательно выбирать из соображений их вероятных,
правдоподобных значений. В качестве
начального приближения выбраны значения : a0 =0.2; b0.=202.0
Приступим к вычислениям опорной прямой, т.е нахождению
коэффициентов а и b в уравнении (1). Для этого
запишем выражение для функционала Ф.
![]()
Число строк
кадра в экспериментальном изображении было равно N=512.
Этот функционал имеет смысл суммы отличий модельных и
экспериментальных позиций края. Условию наилучшего соответствия модели и эксперимента
отвечает минимум этого функционала. Находим его минимум обычным способом: вычисляем
его производные по параметрам модели a и b,
![]() , приравниваем каждую из производных к нулю, разлагаем модельные
массивы координат края в ряды Тейлора:
, приравниваем каждую из производных к нулю, разлагаем модельные
массивы координат края в ряды Тейлора: ![]()
и после тривиальных преобразований получаем систему
двух уравнений с двумя неизвестными: Δа и Δb.
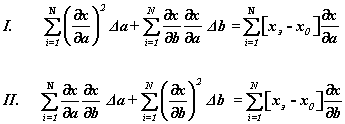
Решение этой системы выполнено по методу Крамера, что
привело к поправкам Δа= - 0.012 и Δb= - 2.0 , введение
которых в начальное приближение
а0 = 0,02 и b0 =202 обеспечило окончательные параметры опорной
прямой в виде: xm(i) = 0.008×i + 200.0
Результат наложения «опорной» прямой на массив экспериментальных координат
края представлен на рисунке 1. Здесь видно, что полученная опорная прямая действительно может служить «репером»
при вычислении разброса (дисперсии) или
СКО экспериментальных координат края.
Расчеты разброса, проведенные на основе полученных параметров опорной
прямой, показывают, что Среднеквадратичное Отклонение, т.е. количественная мера
неровности края в данном случае составляет
0.35 пикселя, что с учетом увеличения микроскопа 500 000х соответствует 0.28 нм.
Литература.
1.
2006 International Technology Roadmap for Semiconductors, (ITRS), SIA.
2. Магнус Я. Р.,
Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс. — М.:
Дело, 2007.
3.
Линник Ю. В. Метод
наименьших квадратов и основы математико-статистической теории обработки наблюдений. М.,
1962.
Рисунки
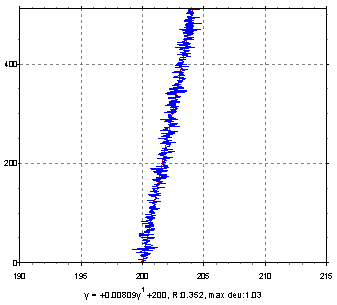
Рисунок 1.
Подпись к рисунку 1.
Наложение фактических координат «прямолинейного» края
наноструктуры,
полученных при увеличениях 500 000х, и опорной прямой линии.