Сатыбалдиев О.С., Мукушева Ж.А.

Қ.И.Сәтбаев атындағы ҚазҰЗТУ, Қазақстан

Математикалық модельдерді пайдаланып

техникалық мазмұнды есептерді шешу

Скважинаның дебиттерін анықтау, скважинаның үйлесімді орналасу жүйесін таңдау, мұнайлы контурлардың орналасуы және т.б. секілді жерасты гидравликасының техникалық есептері математикалық теңдеулердің шешімін табу мәселелеріне алып келеді.

Кез келген мұнай контуры үшін және скважинаның кезкелген орналасуы жағдайында бұл айтылған мәселелердің дәл шешімі жоқ. Алайда, бұл есептерді дұрыс геометриялық формадағы облыстарда қарастыруға болады. Алдымен,

, (1)

теңдеуін қарастыралық.

Бастапқы температурасы берілген және екі шетіндегі температурасы тұрақты стержендегі жылу өткізгіштік теңдеуінің шешімі. Мына мазмұнды есепті қарастыралық. облысында

, (2)

шекаралық шартын және

, (3)

бастапқы шартын қанағаттандыратын (1) теңдеудің шешімін табу қажет болсын. (2) шарт стерженнің және шеттеріндегі сәйкес температуралары мен тұрақты екендігін, ал стерженнің бастапқы температурасы функциясы арқылы өрнектелетіндігін көрсетеді.

Суперпозиция қағидасын қолданып (1) теңдеудің шешуін

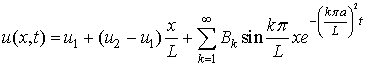(4)

аламыз.

Сым темірдің суу заңдылығы.Температурасы 100⁰С болатын су жылытқышта орналасқан ұзындығы 10 см сым темірді қарастыралық. уақыт моментінде сым темірді судан алып, оның екі шетіндегі температураларын мұздың көмегі арқылы 0 градусқа дейін төмендетелік. Осы жағдайдағы сым темірдің суу заңдылығын ізделік. Қарастырылып отырған есептің шешімі

.

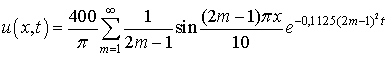болады.

Бір шетіндегі температурасы нөлге тең, екінші шетіндегі температурасы берілген стержендегі жылудың таралуын есептеу. Енді стерженнің сол жақ шетінде жылу жоқ, ал оң жақ шетіндегі жылу барлық мәндері үшін 100⁰С температураны сақтайды деген болжам жасалық.

Бұл болжамның математикалық моделі келесі есеп болып табылады:

(5)

(6)

(7)

Бұл теңдеудің

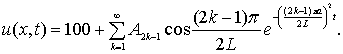(8)

шешімін аламыз.

Шеттеріндегі температуралары әртүрлі стержендегі жылу өткізгіштік теңдеуінің шешімі.

(11)

шекаралық шарттары және

(12)

бастапқы шарты берілген теңдеудің шешімін ізделік. Мұндағы және берілген функциялар.

Есептің шешуін

қатары түрінде іздейміз. Мұндағы

Тікбұрышты формадағы облыстың контурында берілген бастапқы шарттары бойынша мұнай қатпар оның қысымын табу. Тіктөртбұрышты формадағы обылысы берілсін. Осы облыстың контурындағы қысымы

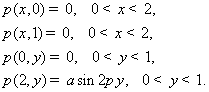
шарттарын қанағаттандырсын. облысындағы мұнай қабатының қысымын табалық.

Мұнай қабатының кезкелген нүктесіндегі қысым , Лаплас теңдеуін қанағаттандыратындығы белгілі. Олай болса бұл есепті төмендегідей тұжырымдауға болады:

шекаралық шарттарды қанағаттандыратын

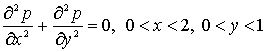
Лаплас теңдеуінің облысындағы шешімін табу керек. Есептің шешімін іздеу үшін айнымалыларды болу әдісін пайдаланамыз. Ол шешім

болады.

Шекарасында берілген қысымның мәндері бойынша жартылай шексіз облыстағы мұнай қатпарының қысымын анықтау. Тағыда бір техникалық мазмұнды қарастыралық. және мәндерінде қысымы нөлге тең және шексіздікке алыстағанда нөлге ұмтылатын, ал қатпардың сол жақ шетінде бірлік қысымды сақтайтын жазық жартылай қатпардағы қысымды анықтау қажет.

Алдымен есеп шартына сәйкес оның математикалық моделін құралық.

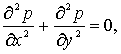
теңдеуінің жазық жартылай қатпар облысының шекарасындағы қысымының мәндеріне сәйкес, яғни

1)

2)

3) шексіздікке ұмтылғанда нөлге ұмтылады,

4)

шарттарын қанағаттандыратын шешімін табу керек.

Ізделіп отырған шешіміміз

болады.

Берілген бастапқы шекаралық шарттары бойынша тіктөртбұрыш облысында мұнай қатпарының кезкелген нүктесіндегі қысымын есептеу. Тағыда бір есепті қарастыралық. облысында Лаплас теңдеуінің

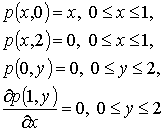
шарттарын қанағаттандыратын шешімін таптық.

Іздеп отырған шешіміміз

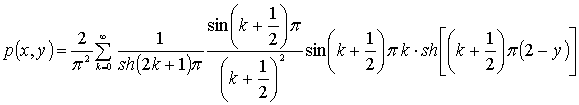болады.

Бұл есептерді шешуде біз төмендегі математикалық аппараттарды пайдаландық:

1. Лаплас түрлендіруі.

2. Жылу таратылу теңдеуі үшін бастапқы шекаралық есептерді шешудегі Фурье әдісі.

3. Жазықтықтағы Лаплас теңдеуі үшін шекаралық есептерді шешу әдістері.

4. Штурм-Лиувилль есебі. Меншікті функциялары бойынша Фурье қатарына жіктеу.

Пайдаланылған әдебиеттер:

1. Яглом И.М. Математические структуры и математическое моделирование. – М.: Наука, 2007.

2. Маскет М. Физические основы технологии добычи нефти. – М.: Институт компьютерных исследований, 2010.