К.ф.-м.н. О.Л. Бозиев

Кабардино-Балкарский государственный университет (г.Нальчик, Россия)

Моделирование динамики популяции нагруженными дифференциальными уравнениями

В работе для решения классической экологической задачи о распространении нового типа организма в активной среде применяется метод редукции к нагруженным уравнениям. Он состоит в замене нелинейного уравнения, моделирующего процесс, ассоциированным с ним нагруженным уравнением и его последующем решении [1]. Найденное приближенное решение затем “уточняется” в ходе некоторого итерационного процесса.

Предположим, что в некотором очаге экологической среды возникает новый тип организма, обладающий лучшей приспособленностью к условиям данной среды. Вследствие активности среды в любой ее точке организмы начинают размножаться немедленно после возникновения, а вне очага размножения организмы появляются в результате диффузии. Необходимо иметь информацию о размере популяции в заданной точке среды в любой момент времени описанного процесса.

Хорошо известно, что простейшей математической моделью динамики популяций является одномерное уравнение Фишера

(1)

с безразмерным параметром a > 0, в котором искомая функция u = u(x,t) представляет плотность популяции, 0 ≤ u ≤ 1. Пусть плотность популяции во всех точках активной среды в момент возникновения нового типа организма, т.е. в момент времени t = 0, задается функцией φ(x), а ее изменение на границах среды x = 0 и x = l за все время процесса определяется через функции ψ₁(t) и ψ₂(t). Математическая формализация приводит к задаче нахождения интегрируемой функции , удовлетворяющей уравнению (1) в области Q = {(x, t): 0 < x < l, 0 < t < T}, а также следующим начальным и граничным условиям при

(2)

Процесс нахождения приближенного решения задачи (1), (2) состоит в последовательной аппроксимации уравнения (1) нагруженными дифференциальными уравнениями. Для этого начальное приближение u⁽⁰⁾(x, t) используется для начала следующего итерационного процесса:

1. При k = 1 решить при соответствующих начальных и граничных условиях уравнение (1), записанное в виде

(3)

2. Полагая k = k + 1 подставить найденную функцию u^(k) в правую часть итерационного уравнения (3) и найти очередное “уточненное” решение u^(k+1).

Процесс завершить при реализации желаемого количества итераций или при достижении заданной точности вычислений.

Для нахождения функции u⁽⁰⁾(x, t) уравнение (1) заменяется аппроксимирующим нагруженным уравнением [1]

(4)

где δ(t) – среднее значение функции u(x, t) на отрезке [0, l]:

Преобразования, подобные проведенным в [2, 3] приводят от (4) к уравнению

al²δ²(t) + 12δ(t) – 6(ψ₁(t) + ψ₂(t)) = 0. (5)

Его корень δ(t) обращает (4) в линейное неоднородное уравнение. Решение задачи (4), (2) примем за начальное приближение u⁽⁰⁾(x, t) в итерационном процессе (3). Решение уравнения (4), как и в последствии уравнений (3), определяется с помощью функции Грина G(x, x, t) для параболического уравнения:

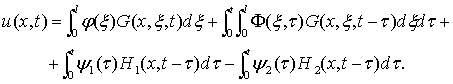(6)

Здесь F(x, t) – правая часть уравнения (4) или (3),

Пример. Пусть φ(x) = lx – x² + 0,5, а ψ₁(t) = ψ₂(t) = 0,5, что соответствует половинной возможной численности популяции на границах среды за все время расчета. Уравнение (5) в этом случае не зависит от t и принимает вид al²δ² + 12δ – 6 = 0. Положим l = 1 и вычислим интегралы в (6) при F(x, t) = –ad ². В результате получим функцию u⁽⁰⁾, которая будет использоваться для начала итерационного процесса (3):

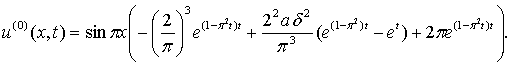
Дальнейшее применение (3) при соответствующих условиях (2) и функции F(x, t) = –a(u^(k-1)(x, t))² в (6) дает формулу общего члена последовательности приближенных решений задачи (1), (2):

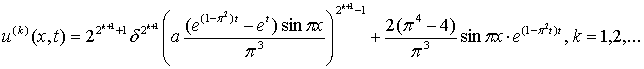Получено аналитическое выражение, позволяющее последовательно аппроксимировать решение задачи (1), (2) функциями u^(k)(x, t), т.е. определять плотность популяции в любой точке среды в требуемый момент наблюдения. Предполагается, что предлагаемый способ может быть эффективным для исследования математических моделей различных биологических и экологических систем, описываемых уравнениями в частных производных.

Литература

1. Нахушев А.М. Нагруженные уравнения и их применение. – М.: Наука, 2012.

2. Бозиев О.Л. Решение начально-краевой задачи для нелинейного параболического уравнения методом редукции к нагруженному уравнению // Известия Кабардино-Балкарского научного центра РАН. 2012, № 4 (48), с. 20–25.

3. Бозиев О.Л. Построение приближенных решений краевых задач для нелинейных дифференциальных уравнений методом редукции к нагруженным уравнениям // Материалы международного симпозиума «Устойчивое развитие: проблемы, концепции, модели», посвященной 20-летию КБНЦ РАН. Россия, Нальчик, 28 июня–3 июля 2013 г. Т. 2, с. 84–87.