К.ф-м.н. Макаричев А.В., Кудь А.А., Щукин А.Б.

Харьковский национальный автомобильно-дорожный университет

Национальный аэрокосмический университет «ХАИ»

О СУММАХ СЛУЧАЙНОГО ЧИСЛА СЛУЧАЙНЫХ СЛАГАЕМЫХ ЗА ВРЕМЯ ОЖИДАНИЯ КАНАЛОМ ОЧЕРЕДНОЙ ЗАЯВКИ В МНОГОЛИНЕЙНОЙ СИСТЕМЕ ОБСЛУЖИВАНИЯ

В многоканальную систему из каналов обслуживания поступает простейший поток заявок с параметром . Время обслуживания заявки имеет показательное распределение с параметром . Нагрузка на систему . Обозначим стационарные вероятности ровно заявок в системе на обслуживании, .

Если в момент поступления очередной заявки в систему в ней есть свободные каналы обслуживания, то пришедшая заявка поступает в тот свободный канал обслуживания, который освободился ранее остальных. Плотность распределения стационарного времени ожидания каналом обслуживания очередной заявки имеет вид

, (1)

где , ,

а -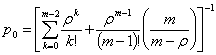

стационарная вероятность отсутствия заявок в системе. Преобразование Лапласа для стационарного времени ожидания каналом очередной заявки на обслуживание представляется в виде функции

.

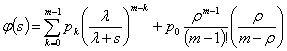Число событий простейшего потока с интенсивностью , возникающих за время ожидания каналом очередной заявки для обслуживания, представляет собой неотрицательную целочисленную случайную величину с распределением

, .

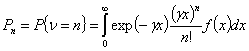Подставляя в эту формулу выражение для плотности (1), имеем

.

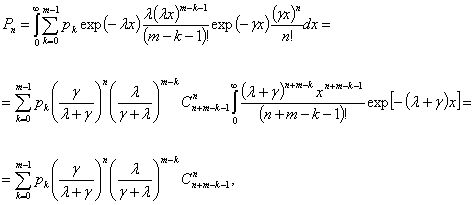
Производящая функция для числа событий, произошедших за время ожидания каналом очередной заявки для обслуживания, представляется в виде функции

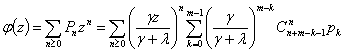, где

, , а

.

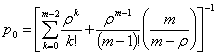Дифференцируя в точке производящую функцию , находим математическое ожидание для числа событий, произошедших за время ожидания каналом очередной заявки для обслуживания

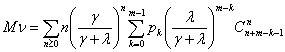
Дисперсия для числа событий, произошедших за время ожидания каналом очередной заявки для обслуживания, из вида производящей функции определяется по формуле

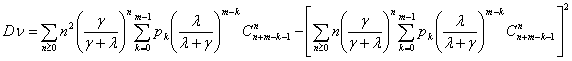
Пусть - последовательность независимых одинаково распределенных случайных величин с конечным вторым моментом, Пусть

- сумма случайного числа случайных слагаемых за время ожидания каналом начала обслуживания очередной заявки,

- характеристическая функция для случайной величины . Тогда характеристическая функция для сумм случайного числа случайных слагаемых за время ожидания каналом начала обслуживания очередной заявки определяется по формуле

.

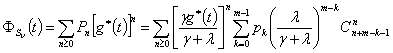Отсюда дифференцированием по параметру в нуле этой характеристической функции определяем математическое ожидание для сумм случайного числа случайных слагаемых за время ожидания каналом начала обслуживания очередной заявки

.

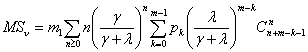Дисперсия этой случайной величины определяется аналогично

.

.

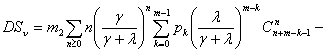
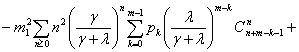
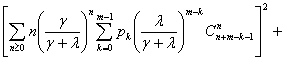
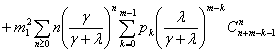Литература.

1. B.V.GNEDENKO AND I.N.KOVALENKO, Introduction to Queueing Theory, Program for Scientific Translations, Jerusalem, 1968.

2. Ширяев А.Н. Вероятность, М.: Наука, 1980, 576 c.