MATHEMATICS / 3. The
probabilities theory and Mathematical Statistics
PhD Iskakova A., Shalkenov Zh.
L.N. Gumilev Eurasian National University, Astana, Kazakhstan
Unbiased
estimation for one discrete distribution of the sum of random variables
Multivariate
model, as a reflection of the current reality, are essential to the description
of many phenomena and situations encountered in daily life. In recent years, we
developed a considerable amount of probabilistic models.
Suppose
that an urn contains balls and each ball in the urn marked some value Lα. Also assume that the
number of possible Lα
there is d.
Let
the elements of the vector p = (p1,
… , pd) determine the
probability of retrieving the ball boxes with respective values L1, … , Ld, and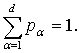 
Produces a sequence of extraction of n balls from the urn with the
return, and it is not known exactly which balls were removed from the box. We
only know the value of u, which
represents the sum of the values taken out of the urn balls. To study this
situation requires the construction of a probability distribution u. Assume that Vu is the number of possible combinations r1vuL1,…, rd vuLd, which
together formed a u, where r1vu,…, rdvu
determine the possible number of balls are removed, that bear the L1, … , Ld. In other words, the number of partitions Vu u on the part of L1, … , Ld. The probability that the random variable U takes the value u, there
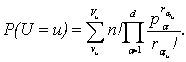(1)
Theorem. A function that
is defined in (1) is a probability distribution.
Let
X = (X1, ..., Xk)
represents a sample and x = (x1, ..., xk). Vectors r1i=(r11i,…, rd1i), …, rVi=(r1Vi,…, rdVi), defining these
partitions, when vi=1,...,
Vi, are solutions of the
following system of equations
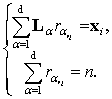(2)
Suppose that for each j = 1, ...,
μ, where 
there exists a vector zj=(z1j,..., zdj), defined as 
and the indices in the right and left side of the
linked-to-one correspondence, which is not unique.
Lemma. a) If any
element of the implementation of the sample x =(x1, ... ,
xk) of the distribution
(1) has more than one partition on a view of the portion, the solutions z1, … , zμ, based
on observation, not implementations are sufficient statistics.
b)
If all the elements of the implementation of the sample x =(x1, ... ,
xk) of the distribution
(1) have no more than one partition on a view of the portion, the solution z1,
based on observation, and is the only implementation of a complete sufficient
statistic.
Theorem. The elements
of W(u, z)={W(u,
z1), …, W(u,
zμ)}
is an unbiased estimate of the probability P (U = u) of the
distribution (1) that for j = 1, ..., μ
is defined as
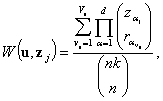(3)
where Vu is the
number of partitions of u on the
part of L1,…, Ld; for each partition r1vu,…, rdvu determine the possible number of balls are removed,
that bear the L1, …, Ld;
k≥1 and zαj≥rαvu, when α = 1, ...,
d, vu=1, …, Vu.
We
have plenty of unbiased estimators (3) for the probability distribution (1).
Consider the problem of determining the most suitable unbiased assessment. By
solving the system of equations (2) we see that for i = 1, ..., k value xi
is partitioned into L1,…, Ld
Vi 1 ways. If Vi > 1, it is unknown what version vi=1, …, Vi additions of works by the corresponding value r1vi, … , rdvi
got value xi. In this
regard, we have many solutions based on observation, and a variety of unbiased
estimates for the probability distribution (1).
Definition.
Decision zg, based on
observation, is the most appropriate of the plurality of z
= { z1, … , zm},
if
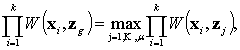(4)
where, for =1, ..., k elements of the
set W(xi, z)={W(xi, z1), … , W(xi,
zm)} is an unbiased estimate of the probability P (U = u) of (1 ) as defined in (3).
Definition.
Unbiased estimation of W (u,
zg)
for the probability P (U = u) distribution (1) is the most
suitable from the entire set of unbiased estimators
W (u, z) = {W (u,
z1), ..., W (u,
zm)},
defined in (3), if zg - the most appropriate
solution based on observation.
Theorem. The most
suitable unbiased estimator W (u,
zg)
for the probability P (U = u) model (1) is consistent,
asymptotically normal and asymptotically efficient.
Thus,
in this work we have the following main results.
1. Proposed a new probability distribution generated urn scheme with balls
labeled by numbers, in the case when observed only their sum.
2. Obtain a set of unbiased estimates for the probability distribution of
the proposed model and the variance of these estimates.
3. Enter the new concept of the most appropriate
assessment of a variety of unbiased estimators having asymptotic properties.
REFERENCES
1. Voinov V.G, Nikulin M.S. Unbiased estimators and their applications M .:
Nauka. 1989. - 440 p.
2. Iskakova AS On a class of discrete multivariate distributions generated
urn scheme with balls labeled rectangular matrices. // Bulletin KazSU Ser.
Mat., Mech., informatics. 2000 ¹1 (94). S. 16-20.